Dieser Beitrag ist von Aki.
ICH Kürzlich habe ich über den Begriff „effektive Stichprobengröße“ gebloggt und auch kommentiert „Ein weiterer wichtiger Punkt ist, dass die effektive Stichprobengröße auch davon abhängt, welche Erwartung geschätzt wird.“ In den Kommentaren fragte Visruth „Warum ergibt E(X^2) ein anderes ESS als E(X)?“ und Kyurae Kim gab die richtige kurze Antwort. Ich habe beschlossen, zusätzliche Illustrationen bereitzustellen
Die NU-Flip-Sampling (NUTS)-Variante des Hamiltonian Monte Carlo (HMC) zielt darauf ab, die erwartete Sprungweite zu maximieren. Die Sprungweite wird nicht genau maximiert, da die Markov-Kette durch Zufälligkeit reversibel bleibt (was eine nützliche Eigenschaft ist, um zu beweisen, dass die stationäre Verteilung die gewünschte Zielverteilung ist) und aufgrund einiger Entscheidungen zur Algorithmuseffizienz. In einigen Fällen kann diese Maximierung der Sprungentfernung zu negativen Autokorrelationen mit ungerader Verzögerung und einer höheren effektiven Stichprobengröße als die Gesamtzahl der Ziehungen führen. Betrachten wir einen Fall, bei dem Theta normalverteilt ist. Befindet sich die Markov-Kette in einem Schwanz, tendiert eine große Sprungdistanz dazu, die Markov-Kette auf die gegenüberliegende Seite der Verteilung zu bringen, und wenn der nächste Sprung ebenfalls eine große Sprungdistanz hat, gehen wir wieder auf die gegenüberliegende Seite und in die Nähe des ersten Punktes. Dann sind Lag 1 und andere ungerade Lag-Autokorrelationen negativ und Lag 2 und andere gerade Lag-Korrelationen positiv. Dadurch wird die effektive Stichprobengröße für E(Theta) größer als die Anzahl der Ziehungen. Als nächstes ist es am einfachsten, eine Normalverteilung mit dem Mittelwert 0 (Vektor von Nullen für multivariate Normalverteilung) zu betrachten, diese lässt sich jedoch auf Mittelwerte ungleich Null verallgemeinern. Wenn wir nun den Absolutwert von abs(Theta) berücksichtigen, wenn wir von Schwanz zu Schwanz springen, ist die Sprungweite wahrscheinlich zu klein und sowohl ungerade als auch gerade Verzögerungsautokorrelationen sind positiv. Damit abs(theta) die Sprungweite maximiert, wäre es besser, zwischen dem Heck- und dem Nahmodus zu springen, aber NUTS ist nicht dafür ausgelegt. Theta^2 verhält sich wie abs(Theta).
Wir können dies mit Stan und einer Stichprobe aus einer multivariaten Normalität testen. Ich probiere eine 16-dimensionale Einheitsnormale aus, da ich weiß, dass bei 16 Dimensionen die Algorithmusdetails darüber, wie die Hamilton-Simulation erweitert und die Kehrtwende entschieden wird, zufällig so sind, dass wir starke destructive Autokorrelationen für Theta erhalten.
information {
int<decrease=0> D; // variety of dimensions
}
parameters {
vector(D) theta;
}
mannequin {
theta ~ regular(0, 1);
}
Und wir führen NUTS mit CmdStanR aus
library(cmdstanr)
mod <- cmdstan_model("regular.stan")
match <- mod$pattern(information=record(D=16), refresh=0)
Im Folgenden untersuche ich nur die erste Dimension von Theta(1)
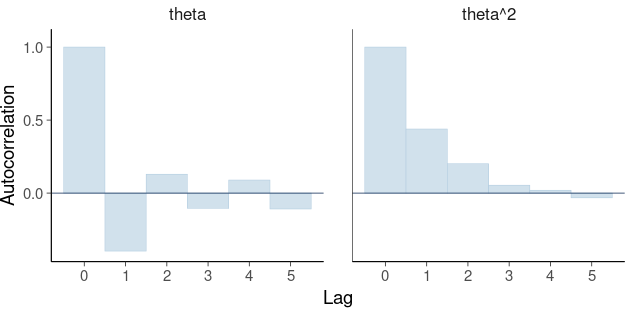
Die Autokorrelationen für Theta und Theta^2 zeigen deutlich, was ich oben beschrieben habe.
Adverse Autokorrelationen führen zu einer Supereffizienz und der geschätzte ESS für Theta beträgt 10457, was 2,6-mal größer ist als die Gesamtzahl der Ziehungen (4000). Der geschätzte ESS für Theta^2 beträgt 1534, was nur 38 % der Gesamtzahl der Ziehungen entspricht! Auch wenn wir nicht direkt an Theta^2 interessiert sind, könnten wir an der SD des hinteren Teils von Theta interessiert sein, und zur Berechnung von SD wird Theta^2 verwendet.
Das folgende Diagramm zeigt den ESS für die Quantile 0,05,…,0,95 (siehe Rangnormalisierung, Faltung und Lokalisierung: Ein verbessertes Rhat zur Beurteilung der Konvergenz von MCMC für die Particulars)
Wir sehen, dass die Genauigkeit der Intervallendpunkte auf einem ESS von etwa 2900 basiert, wenn wir z. B. ein hinteres Intervall von 90 % für Theta melden möchten. Wenn wir additionally ein hinteres SD oder ein hinteres Intervall melden möchten, hat ein sehr hoher ESS für Theta keinen großen Nutzen. Da die Maximierung der Sprungentfernung im Theta-Raum den ESS für Theta^2 und Quantile verringert, verschwenden wir tatsächlich etwas Rechenzeit. Allerdings kommt die multivariate isotrope Normalität bei den meisten interessanten Modellen und Daten nicht so häufig vor, und in den meisten Fällen sehen wir keine negativen Autokorrelationen und kein supereffizientes ESS, und daher besteht kein großer Bedarf, den diesbezüglichen NUTS-Algorithmus zu ändern.
ESS wird zur Schätzung des Monte-Carlo-Standardfehlers verwendet und für jede interessierende Größe, wenn MCSE beispielsweise mithilfe des Posterior-Pakets berechnet wird, wird das entsprechende ESS verwendet. Der Einfachheit halber werden im hinteren Paket auch Bulk-ESS und Tail-ESS gemeldet, die zwei zusammenfassende Werte zur Probenahmeeffizienz im Allgemeinen liefern (siehe das Rhat-Papier für die Particulars). Diese sind als schnelle Zusammenfassungen nützlich, da sie im Gegensatz zu MCSE, das im Kontext der Skala der interessierenden Menge interpretiert werden muss, skalenfrei sind (mehr dazu finden Sie unter die Digits-Fallstudie).