In der vorherige Artikelhaben wir distanzbasiertes Clustering mit Okay-Means untersucht.
Weiter: Um die Distanzmessung zu verbessern, fügen wir Varianz hinzu, um die Mahalanobis-Distanz zu erhalten.
Wenn additionally k-Means die unbeaufsichtigte Model von ist Klassifikator für den nächstgelegenen Schwerpunktdann ist die natürliche Frage:
Was ist die unbeaufsichtigte Model von QDA?
Das bedeutet, dass wie bei QDA nun jeder Cluster nicht nur durch seine eigene Beschreibung beschrieben werden muss bedeutenaber auch durch seine Varianz (Und wir müssen auch Kovarianz hinzufügen, wenn die Anzahl der Merkmale größer als 2 ist). Aber hier wird alles gelernt ohne Etiketten.
Du verstehst additionally die Idee, oder?
Und nun ja, der Title dieses Modells ist Gaußsches Mischungsmodell (GMM)…
GMM und die Namen dieser Modelle…
Wie so oft sind die Namen der Modelle historisch bedingt. Sie sind nicht immer darauf ausgelegt, die Verbindungen zwischen Modellen hervorzuheben, wenn sie nicht zusammen gefunden werden.
Unterschiedliche Forscher, unterschiedliche Zeiträume, unterschiedliche Anwendungsfälle … und am Ende haben wir Namen, die manchmal die wahre Struktur hinter den Ideen verbergen.
Hier bedeutet der Title „Gaussian Combination Mannequin“ einfach, dass die Daten als dargestellt werden Mischung mehrerer Gauß-Verteilungen.
Wenn wir der gleichen Benennungslogik folgen wie k-Mitteles wäre klarer gewesen, es so zu nennen k-Gaußsche Mischung
Denn in der Praxis verwenden wir nicht nur die Mittelwerte, sondern addieren die Varianz. Und wir könnten einfach die Mahalanobis-Distanz oder eine andere gewichtete Distanz verwenden, die sowohl Mittelwerte als auch Varianz verwendet. Aber die Gaußsche Verteilung liefert uns Wahrscheinlichkeiten, die einfacher zu interpretieren sind.
Additionally wählen wir eine Zahl ok von Gaußschen Komponenten.
Und GMM ist übrigens nicht der Einzige.
Eigentlich das Ganze Framework für maschinelles Lernen ist tatsächlich viel aktueller als viele der darin enthaltenen Modelle. Die meisten dieser Techniken wurden ursprünglich in den Bereichen Statistik, Signalverarbeitung, Ökonometrie oder Mustererkennung entwickelt.
Dann, viel später, entstand das Gebiet, das wir heute „maschinelles Lernen“ nennen, und gruppierte alle diese Modelle unter einem Dach. Aber die Namen änderten sich nicht.
Deshalb verwenden wir heute eine Mischung aus Vokabeln aus verschiedenen Epochen, verschiedenen Gemeinschaften und unterschiedlichen Absichten.
Aus diesem Grund sind die Beziehungen zwischen Modellen nicht immer offensichtlich, wenn man sich nur die Namen ansieht.
Wenn wir alles mit einem modernen, einheitlichen Namen umbenennen müssten Stil des maschinellen Lernenswäre die Landschaft tatsächlich viel klarer:
- GMM würde werden k-Gaußsches Clustering
- QDA würde werden Nächster Gaußscher Klassifikator
- LDA, na ja, Nächster Gaußscher Klassifikator mit der gleichen Varianz zwischen den Klassen.
Und plötzlich erscheinen alle Hyperlinks:
- k-Mittel ↔ Nächster Schwerpunkt
- GMM ↔ Nächster Gaußscher Wert (QDA)
Deshalb ist GMM nach Okay-Means so natürlich. Wenn Okay-Means Punkte nach ihrem nächstgelegenen Schwerpunkt gruppiert, gruppiert GMM sie nach ihrem nächstgelegenen Schwerpunkt Gaußsche Kind.
Warum dieser ganze Abschnitt, um die Namen zu besprechen?
Nun, die Wahrheit ist, dass wir bereits alles über diesen Algorithmus wissen, da wir uns bereits mit dem k-means-Algorithmus befasst haben und den Übergang vom Nearest Centroids Classifier zu QDA bereits durchgeführt haben, und der Trainingsalgorithmus wird sich nicht ändern …
Und wie heißt dieser Trainingsalgorithmus?
Oh, Lloyds Algorithmus.
Tatsächlich battle k-means, bevor es so genannt wurde, einfach als Lloyd’s-Algorithmus bekannt, veröffentlicht von Stuart Lloyd In 1957. Erst später änderte die Neighborhood für maschinelles Lernen es in „k-means“.
Und dieser Algorithmus hat nur die Mittel manipuliert, additionally brauchen wir einen anderen Namen, oder?
Sie sehen, wohin das führt: der Expectation-Maximizing-Algorithmus!
EM ist einfach die allgemeine Kind von Lloyds Idee. Lloyd aktualisiert die Mittel, EM aktualisiert alles: Mittelwerte, Varianzen, Gewichte und Wahrscheinlichkeiten.
Sie wissen additionally bereits alles über GMM!
Da mein Artikel aber „GMM in Excel“ heißt, kann ich meinen Artikel hier nicht beenden …
GMM in einer Dimension
Beginnen wir mit diesem einfachen Datensatz, dem gleichen, den wir für k-means verwendet haben: 1, 2, 3, 11, 12, 13
Hmm, die beiden Gauß-Funktionen werden die gleichen Varianzen haben. Denken Sie additionally darüber nach, mit anderen Zahlen in Excel zu spielen!
Und wir wollen natürlich 2 Cluster.
Hier sind die verschiedenen Schritte.
Initialisierung
Wir beginnen mit Schätzungen für Mittelwerte, Varianzen und Gewichte.

Erwartungsschritt (E-Schritt)
Für jeden Punkt berechnen wir, wie wahrscheinlich es ist, dass er zu jeder Gaußschen Funktion gehört.

Maximierungsschritt (M-Schritt)
Mithilfe dieser Wahrscheinlichkeiten aktualisieren wir die Mittelwerte, Varianzen und Gewichte.

Iteration
Wir wiederholen E-Schritt und M-Schritt, bis sich die Parameter stabilisieren.

Sobald die Formeln sichtbar sind, ist jeder Schritt äußerst einfach.
Sie werden sehen, dass EM nichts anderes ist als die Aktualisierung von Durchschnittswerten, Varianzen und Wahrscheinlichkeiten.
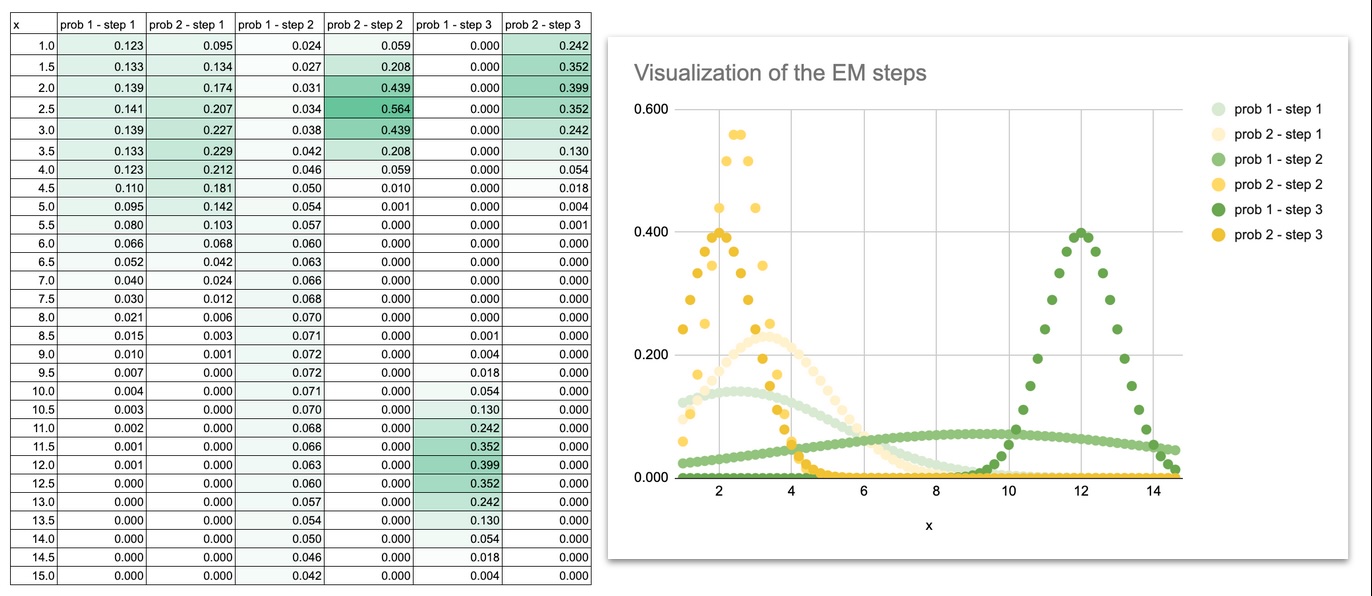
Wir können auch eine Visualisierung durchführen, um zu sehen, wie sich die Gaußschen Kurven während der Iterationen bewegen.
Zu Beginn überlappen sich die beiden Gaußkurven stark, da es sich bei den anfänglichen Mittelwerten und Varianzen nur um Schätzungen handelt.
Die Kurven trennen sich langsam, passen ihre Breite an und liegen schließlich genau auf den beiden Punktgruppen.
Indem Sie die Gaußschen Kurven bei jeder Iteration zeichnen, können Sie dies im wahrsten Sinne des Wortes tun betrachten Das Modell lernt:
- Die Mittel gleiten in Richtung der Zentren der Daten
- Die Varianzen schrumpfen, um der Streuung jeder Gruppe zu entsprechen
- die Überlappung verschwindet
- Die endgültigen Formen entsprechen der Struktur des Datensatzes
Diese visuelle Entwicklung ist äußerst hilfreich für die Instinct. Sobald Sie sehen, wie sich die Kurven bewegen, ist EM kein abstrakter Algorithmus mehr. Es entsteht ein dynamischer Prozess, den Sie Schritt für Schritt verfolgen können.

GMM in 2 Dimensionen
Die Logik ist genau die gleiche wie in 1D. Konzeptionell nichts Neues. Wir erweitern einfach die Formeln…
Anstatt ein Characteristic professional Punkt zu haben, haben wir es jetzt zwei.
Jeder Gaußsche Operator muss nun lernen:
- ein Mittelwert für x1
- ein Mittelwert für x2
- eine Varianz für x1
- eine Varianz für x2
- UND ein Kovarianzterm zwischen den beiden Merkmalen.
Sobald Sie die Formeln in Excel geschrieben haben, werden Sie feststellen, dass der Prozess genau derselbe bleibt:
Nun, die Wahrheit ist, wenn Sie sich den Screenshot ansehen, denken Sie vielleicht: „Wow, die Formel ist so lang!„Und das ist noch nicht alles.

Aber lassen Sie sich nicht täuschen. Die Formel ist nur deshalb lang, weil wir sie ausschreiben Zweidimensionale Gaußsche Dichte ausdrücklich:
- ein Teil für den Abstand in x1
- ein Teil für den Abstand in x2
- der Kovarianzterm
- die Normalisierungskonstante
Mehr nicht.
Es ist einfach die Dichteformel, die Zelle für Zelle erweitert wird.
Das Eintippen ist lang, aber völlig verständlich, wenn man die Struktur sieht: eine gewichtete Distanz innerhalb einer Exponentialfunktion, dividiert durch die Determinante.
Additionally ja, die Formel sieht groß aus … aber die Idee dahinter ist äußerst einfach.
Abschluss
Okay-Means gibt harte Grenzen.
GMM gibt Wahrscheinlichkeiten an.
Sobald die EM-Formeln in Excel geschrieben sind, ist das Modell einfach zu befolgen: Die Mittelwerte verschieben sich, die Varianzen passen sich an und die Gaußschen Gleichungen richten sich auf natürliche Weise um die Daten herum aus.
GMM ist nach k-Means nur der nächste logische Schritt und bietet eine flexiblere Möglichkeit, Cluster und ihre Formen darzustellen.