Der „Adventskalender“-Bonus 1 für maschinelles Lernen: AUC in Excel

wir werden AUC in Excel implementieren.

AUC wird üblicherweise für Klassifizierungsaufgaben als Leistungsmetrik verwendet.

Aber wir beginnen mit einer Verwirrungsmatrix, denn dort beginnt jeder in der Praxis. Dann werden wir sehen, warum eine einzige Verwirrungsmatrix nicht ausreicht.

Und wir beantworten auch diese Fragen:

• AUC bedeutet „Space Below the Curve“, aber unter welcher Kurve?
• Woher kommt diese Kurve?
• Warum ist das Gebiet bedeutungsvoll?
• Ist AUC eine Wahrscheinlichkeit? (Ja, es gibt eine probabilistische Interpretation)

1. Warum eine Verwirrungsmatrix nicht ausreicht

1.1 Ergebnisse von Modellen

Ein Klassifikator gibt uns normalerweise Auskunft Partiturenkeine endgültigen Entscheidungen. Die Entscheidung fällt später, wenn wir einen Schwellenwert festlegen.

Wenn Sie die vorherigen „Adventskalender“-Artikel gelesen haben, haben Sie bereits gesehen, dass „Punktzahl“ je nach Modellfamilie unterschiedliche Bedeutungen haben kann:

• Distanzbasierte Modelle (wie k-NN) berechnen oft den Anteil der Nachbarn für eine bestimmte Klasse (oder eine distanzbasierte Konfidenz), was zu einem Rating wird.
• Dichtebasierte Modelle Berechnen Sie eine Wahrscheinlichkeit für jede Klasse und normalisieren Sie sie dann, um eine endgültige (posteriore) Wahrscheinlichkeit zu erhalten.
• Einstufung Baumbasierte Modelle Geben Sie häufig den Anteil einer bestimmten Klasse an den Trainingsbeispielen innerhalb des Blattes aus (aus diesem Grund haben viele Punkte die gleiche Punktzahl).
• Gewichtsbasierte Modelle (lineare Modelle, Kernel, neuronale Netze) berechnen eine gewichtete Summe oder einen nichtlinearen Rating und wenden manchmal einen Kalibrierungsschritt (Sigmoid, Softmax, Platt-Skalierung usw.) an, um ihn einer Wahrscheinlichkeit zuzuordnen.

Unabhängig von der Herangehensweise landen wir additionally in der gleichen Scenario: eine Punktzahl professional Beobachtung.

In der Praxis wählen wir dann oft einen Schwellenwert 0,5und wir konvertieren Ergebnisse in vorhergesagte Klassen.

Und genau hier kommt die Verwirrungsmatrix ins Spiel.

1.2 Die Verwirrungsmatrix an einer Schwelle

Sobald ein Schwellenwert festgelegt ist, wird jede Beobachtung zu einer binären Entscheidung:

• vorhergesagt positiv (1) oder vorhergesagt negativ (0)

Daraus können wir vier Zahlen zählen:

• TP (True Positives): vorhergesagt 1 und tatsächlich 1
• TN (True Negatives): vorhergesagt 0 und tatsächlich 0
• FP (False Positives): vorhergesagt 1, aber tatsächlich 0
• FN (False Negatives): vorhergesagt 0, aber tatsächlich 1

Diese 2×2-Zähltabelle ist die Verwirrungsmatrix.

Dann berechnen wir typischerweise Verhältnisse wie:

• Präzision = TP / (TP + FP)
• Rückruf (TPR) = TP / (TP + FN)
• Spezifität = TN / (TN + FP)
• FPR = FP / (FP + TN)
• Genauigkeit = (TP + TN) / Gesamt

Bisher ist alles sauber und intuitiv.

Es gibt jedoch eine versteckte Einschränkung: Alle diese Werte hängen vom Schwellenwert ab. Die Verwirrungsmatrix bewertet additionally das Modell an einem Betriebspunkt, nicht das Modell selbst.

1.3 Wenn eine Schwelle alles durchbricht

Dies ist ein seltsames Beispiel, aber es macht den Punkt dennoch sehr deutlich.

Stellen Sie sich vor, Ihr Schwellenwert ist auf 0,50 festgelegt und alle Werte liegen unter 0,50.

Dann sagt der Klassifikator Folgendes voraus:

• Positiv vorhergesagt: keine
• Voraussichtliches Negativ: alle

Sie erhalten additionally:

• TP = 0, FP = 0
• FN = 10, TN = 10

Dies ist eine vollkommen gültige Verwirrungsmatrix. Es erzeugt auch ein sehr seltsames Gefühl:

• Präzision wird #DIV/0! weil es keine vorhergesagten positiven Ergebnisse gibt.
• Der Rückruf beträgt 0 %, da Sie keine positiven Ergebnisse erzielt haben.
• Die Genauigkeit liegt bei 50 %, was „nicht schlecht“ klingt, auch wenn das Modell nichts gefunden hat.

An der Verwirrungsmatrix ist nichts auszusetzen. Das Drawback ist die Frage, die wir ihm gestellt haben.

Eine Verwirrungsmatrix antwortet: „Wie intestine ist das Modell bei diesem bestimmten Schwellenwert?“

Wenn der Schwellenwert schlecht gewählt ist, kann die Verwirrungsmatrix ein Modell nutzlos erscheinen lassen, selbst wenn die Ergebnisse eine echte Trennung enthalten.

Und in Ihrer Tabelle ist die Trennung sichtbar: Constructive haben oft Werte um 0,49, Unfavorable eher um 0,20 oder 0,10. Das Modell ist nicht zufällig. Ihr Schwellenwert ist einfach zu streng.

Deshalb reicht ein einzelner Schwellenwert nicht aus.

Was wir stattdessen brauchen, ist eine Möglichkeit, das Modell zu bewerten über Schwellen hinwegnicht bei einem einzigen.

2. ROC

Zuerst müssen wir die Kurve erstellen, da AUC für „Space Below a Curve“ steht, additionally müssen wir diese Kurve verstehen.

2.1 Was ROC bedeutet (und was es ist)

Denn die erste Frage, die sich jeder stellen sollte, lautet: AUC unter welcher Kurve?

Die Antwort lautet:

AUC ist die Fläche unter der ROC-Kurve.

Aber das wirft eine andere Frage auf.

Was ist die ROC-Kurve und woher kommt sie?

ROC steht für Betriebseigenschaften des Empfängers. Der Identify ist historisch (frühe Signalerkennung), aber die Idee ist fashionable und einfach: Sie beschreibt, was passiert, wenn Sie die Entscheidungsschwelle ändern.

Die ROC-Kurve ist ein Diagramm mit:

• x-Achse: FPR (Falsch-Positiv-Charge)
  FPR = FP / (FP + TN)
• y-Achse: TPR (True Constructive Charge), auch Recall oder Sensitivität genannt
  TPR = TP / (TP + FN)

Jeder Schwellenwert gibt einen Punkt (FPR, TPR). Wenn Sie alle Punkte verbinden, erhalten Sie die ROC-Kurve.

In diesem Stadium ist ein Element wichtig: Die ROC-Kurve wird nicht direkt beobachtet; Es wird konstruiert, indem der Schwellenwert über die Bewertungsreihenfolge gestrichen wird.

2.2 Aufbau der ROC-Kurve aus Scores

Für jede Punktzahl können wir sie als Schwellenwert verwenden (und natürlich könnten wir auch benutzerdefinierte Schwellenwerte definieren).

Für jeden Schwellenwert:

• Wir berechnen TP, FP, FN, TN aus der Verwirrungsmatrix
• dann berechnen wir FPR und TPR

Die ROC-Kurve ist additionally einfach die Sammlung all dieser (FPR, TPR)-Paare, geordnet von strengen Schwellenwerten bis hin zu freizügigen Schwellenwerten.

Genau das werden wir in Excel umsetzen.

An diesem Punkt ist es wichtig, etwas zu bemerken, das sich quick zu einfach anfühlt. Wenn wir die ROC-Kurve erstellen, spielen die tatsächlichen numerischen Werte der Bewertungen keine Rolle. Was zählt, ist das Befehl.

Wenn ein Modell Werte zwischen 0 und 1 ausgibt, ein anderes Modell Werte zwischen -12 und +5 und ein drittes nur zwei unterschiedliche Werte ausgibt, funktioniert ROC auf die gleiche Weise. Solange höhere Werte tendenziell der positiven Klasse entsprechen, wird der Schwellenwert-Sweep die gleiche Reihenfolge von Entscheidungen erzeugen.

Aus diesem Grund ist der erste Schritt in Excel immer derselbe: Sortieren Sie nach der Punktzahl vom höchsten zum niedrigsten. Sobald die Zeilen in der richtigen Reihenfolge sind, zählt der Relaxation nur noch.

2.3 Lesen der ROC-Kurve

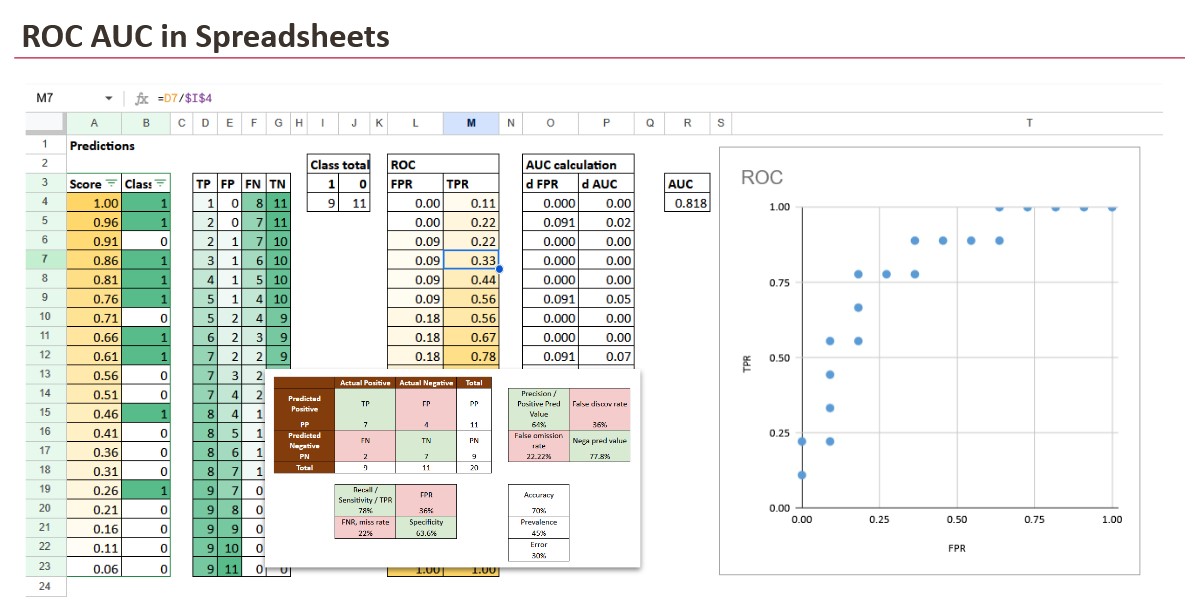
In der Excel-Tabelle wird die Konstruktion sehr konkret.

Sie sortieren Beobachtungen nach Punktzahl, vom höchsten zum niedrigsten. Dann gehen Sie die Liste durch. In jeder Zeile verhalten Sie sich so, als ob der Schwellenwert auf diesen Wert festgelegt wäre, was bedeutet, dass alles darüber als positiv vorhergesagt wird.

Dadurch kann Excel kumulative Zählungen berechnen:

• Wie viele optimistic Rückmeldungen haben Sie bisher angenommen?
• Wie viele Unfavorable haben Sie bisher akzeptiert?

Aus diesen kumulativen Zählungen und den Datensatzsummen berechnen wir TPR und FPR.

Jetzt ist jede Zeile ein ROC-Punkt.

Warum die ROC-Kurve wie eine Treppe aussieht

• Wenn die nächste akzeptierte Zeile positiv ist, erhöht sich TP, sodass TPR zunimmt, während FPR flach bleibt.
• Wenn die nächste akzeptierte Zeile negativ ist, erhöht sich FP, sodass FPR zunimmt, während TPR flach bleibt.

Aus diesem Grund ist die ROC-Kurve bei realen endlichen Daten eine Treppe. Excel macht dies sichtbar.

2.4 Referenzfälle, die Sie kennen sollten

Ein paar Referenzfälle helfen Ihnen, die Kurve sofort zu lesen:

• Perfekte Klassifizierung: Die Kurve verläuft gerade nach oben (TPR erreicht 1, während FPR 0 bleibt) und geht dann ganz nach oben.

• Zufälliger Klassifikator: Die Kurve bleibt nahe der Diagonalen von (0,0) nach (1,1).

• Invertierte Rangfolge: Die Kurve fällt „unter“ die Diagonale und die AUC wird kleiner als 0,5. Aber in diesem Fall müssen wir die Punktzahlen mit 1-Punktzahl ändern. Theoretisch können wir diesen fiktiven Fall betrachten. In der Praxis geschieht dies meist dann, wenn Ergebnisse in die falsche Richtung interpretiert oder Klassenbezeichnungen vertauscht werden.

Das sind nicht nur Theorien. Sie sind visuelle Anker. Sobald Sie sie haben, können Sie jede echte ROC-Kurve schnell interpretieren.

3. ROC AUC

Was können wir nun mit der Kurve tun?

3.1 Berechnung der Fläche

Sobald die ROC-Kurve als Liste von Punkten (FPR, TPR) vorliegt, ist die AUC reine Geometrie.

Zwischen zwei aufeinanderfolgenden Punkten ergibt sich als addierte Fläche die Fläche eines Trapezes:

• Breite = Änderung des FPR
• Höhe = durchschnittlicher TPR der beiden Punkte

In Excel wird dies zu einem „Delta-Spalten“-Ansatz:

• Berechnen Sie dFPR zwischen aufeinanderfolgenden Zeilen
• mit dem durchschnittlichen TPR multiplizieren
• alles zusammenfassen

Verschiedene Fälle:

• perfekte Klassifizierung: AUC = 1
• zufällige Rangfolge: AUC ≈ 0,5
• invertierte Rangfolge: AUC < 0,5

Die AUC ist additionally buchstäblich die Zusammenfassung der gesamten ROC-Stufe.

3.2. AUC als Wahrscheinlichkeit

Bei der AUC geht es nicht darum, einen Schwellenwert festzulegen.

Es beantwortet eine viel einfachere Frage:

Wenn ich zufällig ein positives und ein negatives Beispiel auswähle, wie groß ist dann die Wahrscheinlichkeit, dass das Modell dem positiven Beispiel eine höhere Punktzahl zuweist?

Das ist alles.

• AUC = 1,0 bedeutet perfektes Rating (das Constructive bekommt immer eine höhere Punktzahl)

• AUC = 0,5 bedeutet zufällige Rangfolge (es ist im Grunde ein Münzwurf)

• AUC < 0,5 bedeutet, dass die Rangfolge umgekehrt ist (Unfavorable erhalten tendenziell höhere Werte)

Diese Interpretation ist äußerst nützlich, da sie diesen wichtigen Punkt noch einmal erklärt:

Die AUC hängt nur von der Reihenfolge der Ergebnisse ab, nicht von den absoluten Werten.

Aus diesem Grund funktioniert ROC AUC auch dann, wenn die „Scores“ nicht perfekt kalibrierte Wahrscheinlichkeiten sind. Dabei kann es sich um Rohwerte, Ränder, Blattproportionen oder einen beliebigen monotonen Konfidenzwert handeln. Solange höher „wahrscheinlicher positiv“ bedeutet, kann AUC die Rankingqualität bewerten.

Abschluss

Eine Verwirrungsmatrix bewertet ein Modell bei einem Schwellenwert, aber Klassifikatoren erzeugen Bewertungen, keine Entscheidungen.
ROC und AUC bewerten das Modell über alle Schwellenwerte hinweg, indem sie sich darauf konzentrieren Rangkeine Kalibrierung.

Am Ende beantwortet AUC eine einfache Frage: Wie oft erhält ein positives Beispiel eine höhere Punktzahl als ein negatives?
So gesehen ist ROC AUC eine intuitive Metrik, und eine Tabelle reicht aus, um jeden Schritt explizit zu machen.