Erweiterte Vektorindizierungstechniken für hochdimensionale Daten

Einführung

In der heutigen datenorientierten Gesellschaft sind hochdimensionale Datenvektoren wichtiger denn je für verschiedene Anwendungen wie Empfehlungssysteme, Bilderkennung, NLPUnd Anomalieerkennung. Eine effiziente Suche in diesen Vektoren kann schwierig sein, insbesondere bei Datensätzen mit Millionen oder Milliarden von Vektoren. Es sind fortgeschrittenere Indizierungstechniken erforderlich, da herkömmliche Methoden wie B-Bäume und Hash-Tabellen für diese Situationen nicht ausreichen.

Vektordatenbanken, die für die Handhabung und Suche von Vektoren entwickelt wurden, erfreuen sich aufgrund ihrer hohen Suchgeschwindigkeit großer Beliebtheit. Diese ist auf die von ihnen verwendeten Indizierungsmethoden zurückzuführen. In diesem Weblog werden die fortgeschrittenen Vektorindizierungsmethoden näher untersucht, die diese Datenbanken unterstützen und blitzschnelle Suchvorgänge selbst in hochdimensionalen Räumen gewährleisten.

Lernziele

• Erfahren Sie, wie wichtig die Vektorindizierung bei der hochdimensionalen Suche ist.
• Lernen Sie die wichtigsten Methoden der Indizierung für effektive Suchen kennen, wie zum Beispiel Produktquantisierung (PQ), Approximate Nearest Neighbor Search (ANNS) und HNSW (Hierarchical Navigable Small World-Graphen).
• Erfahren Sie, wie Sie diese Indizierungstechniken mit Python-basierten Bibliotheken wie FAISS implementieren.
• Erkunden Sie die Optimierungsstrategien, um effiziente Abfragen und Abrufe im großen Maßstab sicherzustellen.

Dieser Artikel erschien im Rahmen der Information Science-Blogathon.

Herausforderungen der hochdimensionalen Vektorsuche

Bei der Suche nach den nächsten Nachbarn eines Abfragevektors in der Vektorsuche wird die „Nähe“ mithilfe von Metriken wie euklidischer Distanz, Kosinusähnlichkeit oder anderen Distanzmetriken gemessen. Brute-Power-Methoden werden mit zunehmender Datendimensionalität rechenintensiver und erfordern häufig eine lineare Zeitkomplexität, die O(n) beträgt, wobei n die Anzahl der Vektoren darstellt.

Der berüchtigte Fluch der Dimensionalität verschlechtert die Leistung, indem er Distanzmetriken weniger aussagekräftig macht und den Abfrageaufwand weiter erhöht. Dies macht spezielle Vektorindizierungsmechanismen erforderlich.

Erweiterte Indizierungstechniken

Eine effektive Indizierung reduziert den Suchraum, indem sie Strukturen erstellt, die ein schnelleres Abrufen ermöglichen. Zu den wichtigsten Techniken gehören:

Produktquantisierung (PQ)

Produktquantisierung (PQ) ist eine fortschrittliche Technik, die hochdimensionale Vektoren komprimiert, indem sie in Unterräume aufgeteilt und jeder Unterraum unabhängig quantisiert wird. Dadurch können wir die Geschwindigkeit von Ähnlichkeitssuchaufgaben erhöhen und den benötigten Speicherbedarf erheblich reduzieren.

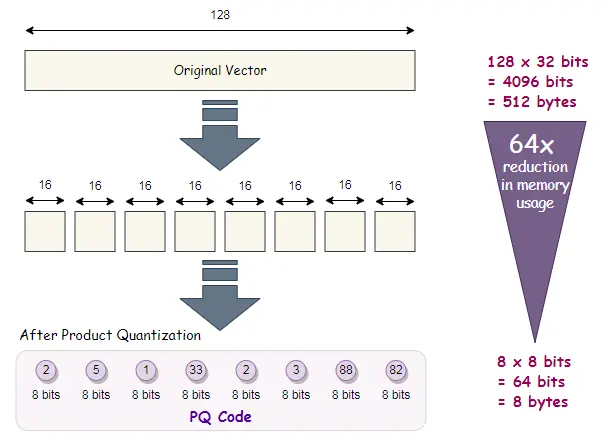
Wie funktioniert PQ?

• Aufteilen des Vektors: Der Vektor wird in m kleinere Untervektoren aufgeteilt.
• Quantisierung: Jeder Untervektor wird unabhängig mithilfe eines kleinen Codebuchs (Satz von Schwerpunkten) quantisiert.
• Komprimierte Darstellung: Die resultierende komprimierte Darstellung ist eine Kombination der quantisierten Untervektoren, die eine effiziente Speicherung und Suche ermöglicht.

PQ-Umsetzung mit FAISS

import numpy as np
import faiss
# Create a random set of vectors (measurement: 10000 vectors of 128 dimensions)
dimension = 128
n_vectors = 10000
knowledge = np.random.random((n_vectors, dimension)).astype('float32')
# Create a product quantizer index in FAISS
quantizer = faiss.IndexFlatL2(dimension)  # L2 distance quantizer
index = faiss.IndexIVFPQ(quantizer, dimension, 100, 8, 8)  # PQ index with 8 sub-vectors

# Prepare the index together with your knowledge
index.prepare(knowledge)
# Add vectors to the index
index.add(knowledge)
# Carry out a seek for the closest neighbors
query_vector = np.random.random((1, dimension)).astype('float32')
distances, indices = index.search(query_vector, 5)
print(f"Nearest neighbors (indices): {indices}")
print(f"Distances: {distances}")

Ausgabe:

In diesem Code nutzen wir FAISS, eine von Fb AI Analysis erstellte Bibliothek, um eine Produktquantisierung durchzuführen. Wir erstellen zunächst einen zufälligen Satz von Vektoren, trainieren den Index und verwenden ihn dann für die Vektorsuche.

Vorteile von PQ

• Speichereffizienz: PQ reduziert den Speicherverbrauch durch Komprimieren von Vektoren erheblich.
• Geschwindigkeit: Die Suche nach komprimierten Daten ist schneller als die Suche nach vollständigen Vektoren.

Ungefähre Suche nach nächsten Nachbarn (ANNS)

ANNS bietet eine Methode, um Vektoren zu lokalisieren, die einem Abfragevektor „ungefähr“ am nächsten liegen, wobei etwas Präzision zugunsten einer deutlichen Geschwindigkeitssteigerung geopfert wird. Die beiden am häufigsten verwendeten ANNS-Methoden sind LSH (Locality Delicate Hashing) und IVF (Inverted File Index).

Invertierter Dateiindex (IVF)

IVF unterteilt den Vektorraum in mehrere Partitionen (oder Cluster). Anstatt den gesamten Datensatz zu durchsuchen, wird die Suche auf Vektoren beschränkt, die in einige relevante Cluster fallen.

Durchführung einer IVF mit FAISS

# Similar dataset as above
quantizer = faiss.IndexFlatL2(dimension)
index_ivf = faiss.IndexIVFFlat(quantizer, dimension, 100)  # 100 clusters

# Prepare the index
index_ivf.prepare(knowledge)
# Add vectors to the index
index_ivf.add(knowledge)
# Carry out the search
index_ivf.nprobe = 10  # Search 10 clusters
distances, indices = index_ivf.search(query_vector, 5)
print(f"Nearest neighbors (indices): {indices}")
print(f"Distances: {distances}")

Ausgabe:

In diesem Code haben wir einen invertierten Dateiindex erstellt und die Suche auf eine begrenzte Anzahl von Clustern beschränkt (gesteuert durch den Parameter nprobe).

Vorteile von ANNS

• Sublineare Suchzeit: Durch die Einschränkung des Suchraums können ANNS-Methoden eine nahezu konstante Suchzeit erreichen, wodurch die Verarbeitung sehr großer Datensätze möglich wird.
• Anpassbarer Kompromiss: ANSS-Methoden bieten den benutzerdefinierten Kompromiss, um Parameter wie nprobe in FAISS zu optimieren und so ein Gleichgewicht zwischen Geschwindigkeit und Suchgenauigkeit herzustellen.

Hierarchisch navigierbare kleine Welt (HNSW)

HNSW ist eine graphenbasierte Methode, bei der Vektoren in einen Graphen eingefügt werden, die jeden Knoten mit seinen nächsten Nachbarn verbinden. Die Erkundung erfolgt, indem man sich von einem zufällig ausgewählten Knoten aus gierig durch den Graphen bewegt. Wir haben:

• Mehrschichtiges Diagramm: Der Graph besteht aus mehreren Schichten. Um eine schnelle Navigationssuche zu ermöglichen, sind die unteren Schichten dicht und die oberen Schichten dünn miteinander verbunden.
• Gierige Suche: Die Suche beginnt in der obersten Ebene und bewegt sich schrittweise nach unten, bis sie auf die nächsten Nachbarn eingegrenzt wird.

Implementierung von HNSW mit FAISS

# HNSW index in FAISS
index_hnsw = faiss.IndexHNSWFlat(dimension, 32)  # 32 is the connectivity parameter
# Add vectors to the index
index_hnsw.add(knowledge)
# Carry out the search
distances, indices = index_hnsw.search(query_vector, 5)
print(f"Nearest neighbors (indices): {indices}")
print(f"Distances: {distances}")

Ausgabe

Es hat sich gezeigt, dass HNSW hinsichtlich der Suchgeschwindigkeit eine erstklassige Leistung liefert und gleichzeitig hohe Rückrufraten aufrechterhält.

Vorteile von HNSW

• Hocheffizient für große Datensätze: Es bietet eine logarithmische Skalierung der Suchzeit in Bezug auf die Datensatzgröße.
• Dynamische Updates: Neue Vektoren können effizient hinzugefügt werden, ohne den gesamten Index neu zu trainieren.

Optimieren von Vektorindizes für eine realistische Leistung

Lassen Sie uns nun darüber sprechen, wie Vektorindizes für eine realistische Leistung optimiert werden können.

Distanzmetriken

Die Auswahl der Distanzmessung (wie euklidische oder Kosinus-Ähnlichkeit) beeinflusst das Ergebnis stark. Forscher verwenden häufig Kosinus-Ähnlichkeit für Texteinbettungen, während sie sich bei Bild- und Audiovektoren oft auf die euklidische Distanz verlassen.

Optimieren von Indexparametern

Jede Indizierungsmethode hat ihre anpassbaren Parameter. Zum Beispiel:

• nprobe für IVF.
• Untervektorgröße für PQ.
• Konnektivität für HNSW.

Um einen Kompromiss zwischen Geschwindigkeit und Rückruf zu finden, ist die richtige Abstimmung dieser Parameter von entscheidender Bedeutung.

Abschluss

Die Beherrschung der Vektorindizierung ist für den Aufbau leistungsstarker Suchsysteme unerlässlich. Während die Suche mit roher Gewalt über große Datensätze ineffizient ist, ermöglichen fortschrittliche Techniken wie Produktquantisierung, Approximate Nearest Neighbor Search und HNSW ultraschnelle Abfragen ohne Kompromisse bei der Genauigkeit. Durch den Einsatz von Instruments wie FAISS und die Feinabstimmung von Indexparametern können Entwickler skalierbare Systeme erstellen, die Millionen von Vektoren verarbeiten können.

Die wichtigsten Erkenntnisse

• Durch die Vektorindizierung wird die Suchzeit drastisch reduziert und Vektordatenbanken hocheffizient gemacht.
• Die Produktquantisierung komprimiert Vektoren für einen schnelleren Abruf, während ANNS und HNSW die Suche durch Einschränkung des Suchraums optimieren.
• Vektordatenbanken sind skalierbar und flexibel und daher in verschiedenen Branchen einsetzbar, von E-Commerce und Empfehlungssystemen bis hin zu Bildabruf, NLP und Anomalieerkennung. Die richtige Wahl des Vektorindex kann bei bestimmten Anwendungsfällen zu Leistungsverbesserungen führen.

Häufig gestellte Fragen

Die in diesem Artikel gezeigten Medien sind nicht Eigentum von Analytics Vidhya und werden nach Ermessen des Autors verwendet.