Das ist Erik. Wenn uns das Glück schenkt, erhalten wir möglicherweise einen unverzerrten, normalverteilten Schätzer mit Standardfehlern für einen (unbekannten) Parameter von Interesse, Theta. Hier gehen wir sogar davon aus, dass s bekannt ist. Der Unterschied zwischen dem Wissen von s und der Notwendigkeit, es schätzen zu müssen, ist der Unterschied zwischen einem t-Check und einem z-Check. Das ist ein kleiner Unterschied, wenn es keine schwerwiegenden Ausreißer gibt und die Stichprobengröße nicht zu klein ist. Hoffen wir additionally einfach das Beste und nehmen an, dass y die Normalverteilung mit mittlerem Theta und Standardabweichung s hat. Das 95 %-Konfidenzintervall für Theta beträgt y ± 1,96 × s. Alles sehr Commonplace.
Die Z-Statistik ist das Verhältnis des Schätzers zu seinem Standardfehler, additionally z=y/s. Daraus folgt, dass z die Normalverteilung mit dem Mittelwert Theta/s und der Standardabweichung 1 hat. Es scheint in der Statistik keinen guten Namen für Theta/s zu geben, additionally das Verhältnis des wahren Parameters zum Standardfehler seines Schätzers. Wir könnten uns jedoch einen Begriff aus der Technik leihen: den Sign-Rausch-Verhältnis oder SNR. Definieren wir additionally SNR=Theta/s. Dann hat die Z-Statistik die Normalverteilung mit mittlerem SNR und Standardabweichung 1.
Das SNR ist leicht zu interpretieren. Wenn Theta=0, dann ist auch das SNR Null. SNR=1 (oder -1) bedeutet, dass der Parameter, den wir schätzen möchten, ungefähr die gleiche Größe hat wie das Rauschen in unserem Schätzer. Das ist keine sehr günstige State of affairs. Beispielsweise besteht eine Wahrscheinlichkeit von 16 %, dass der Schätzer ein anderes Vorzeichen als der wahre Parameter hat. Das liegt daran
P(y < 0 | SNR=1) = P(z < 0 | SNR=1) = pnorm(0,1,1)=0,16.
Wenn SNR = 2,8 (oder -2,8), beträgt die Wahrscheinlichkeit, die Hypothese, dass Theta = 0 ist, abzulehnen, 80 % (Alpha = 0,05 zweiseitig). Das liegt daran
P(|z|>1,96 | SNR=2,8)=pnorm(-1.96,2.8,1) + 1 – pnorm(1.96,2.8,1) = 0,8.
Es besteht eine 1:1-Beziehung zwischen der absoluten Z-Statistik und dem zweiseitigen p-Wert zum Testen der Hypothese, dass Theta = 0 ist. In R haben wir z=qnorm(1-p/2) Und p=2*pnorm(-abs(z)).Dennoch gefallen mir Z-Statistiken aufgrund ihrer direkten Beziehung zum SNR besser als p-Werte. Tatsächlich können wir uns die Z-Statistik als eine Schätzung des SNR mit Standardfehler 1 vorstellen. Das SNR und die Z-Statistik sagen etwas über die Qualität eines Experiments aus, ohne Bezug auf Hypothesentests.
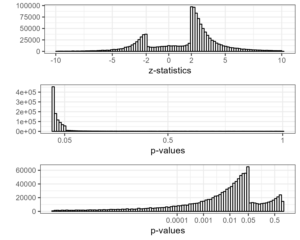
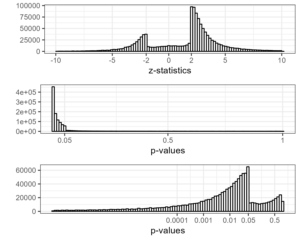
Vor ein paar Tagen habe ich gepostet ein Histogramm der Z-Statistiken von PubMed und habe das Fehlen von Z-Statistiken zwischen -2 und 2 festgestellt. Ich habe jetzt auch Histogramme der entsprechenden zweiseitigen p-Werte erstellt, mit und ohne logarithmisch transformierte Achse. Diese zeigen erwartungsgemäß einen steilen Abfall bei 0,05. Für mich ist das Histogramm der Z-Statistik am einfachsten zu lesen. Man könnte sogar sagen, dass der p-Wert eine Verzerrung der z-Statistik darstellt. Oder meinst du, das geht zu weit?