John Cook dinner schreibt:
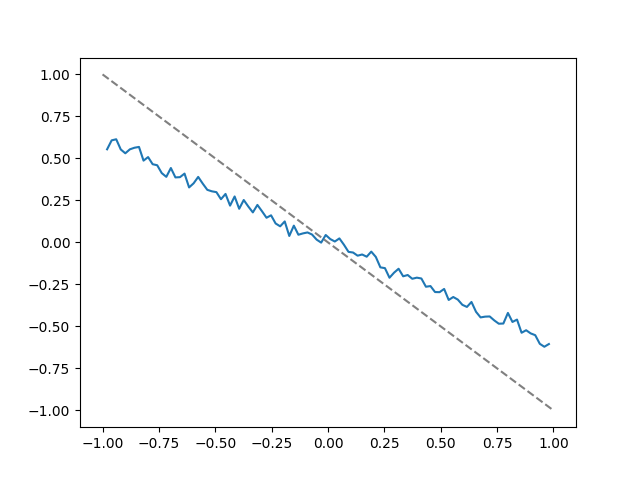
Im Prozess des Schreibens mein neuster Beitrag Ich bin auf die Beobachtung gestoßen, dass die Schiefe der linearen Korrelation proportional zur Korrelation ist. Hast du das schon einmal gesehen? Ich gehe davon aus, dass es allgemein bekannt ist, wenn es wahr ist. Scheinbar stimmt es zumindest annähernd.
Das obige Diagramm aus Cooks Beitrag stammt aus einer Simulation mit n=100.
Ich antwortete, dass dieses Ergebnis plausibel erscheint. Ich denke, eine Möglichkeit, eine Vorstellung davon zu bekommen, besteht darin, den Extremfall zu betrachten, bei dem rho = 1 – Epsilon für ein sehr kleines Epsilon ist. Dort sollte es möglich sein, die Verteilung analytisch zu ermitteln. Es ist lustig – wir reden über Schiefe, aber ich denke normalerweise nicht über den numerischen Wert der Schiefe nach.
Außerdem arbeite ich bei der Betrachtung von Transformationen normalerweise in einem Regressionskontext und mein Ziel ist es, die Beziehung so zu transformieren, dass sie näher an Additivität und Linearität liegt. nicht um eine symmetrische oder normale Verteilung von Rohdaten oder Residuen zu erhalten. Obwohl ich das Ergebnis aus mathematischer und theoretischer Sicht faszinierend finde, denke ich, dass Bedenken hinsichtlich der Schiefe oft überbewertet werden, wenn sie in der statistischen Analyse auftauchen!
John antwortete:
Vereinbart. Für mich ist es eine gelbe Flagge, wenn ich jemanden über Schiefe und Wölbung reden höre.
Das Ergebnis ist nicht wichtig, aber ich finde es merkwürdig, dass es so einfach ist. Es ist bekannt, dass die Verteilung mit zunehmendem Rho weniger regular wird, aber offenbar wird sie auf eine Weise weniger regular, die sich zumindest annähernd trivial beschreiben lässt.
Es amüsierte mich, dass er dies als „gelbe Flagge“ bezeichnete. Das ist so bezaubernd präzise! Der übliche Ausdruck ist „rote Fahne“, aber John hat recht, wenn es um Schiefe und Korrelation geht, ist das nicht wirklich eine rote Fahne; Es handelt sich um ein eher mildes Downside, daher „gelbe Flagge“. Als Statistiker schätze ich diese Präzision in der Kommunikation.
Aber zurück zur Forschungsfrage. Ich gehe davon aus, dass die Beziehung nicht gerade linear ist, selbst im Grenzbereich von großem N, aber wer weiß? Ich denke, ein Ausgangspunkt wäre die Bewertung der Schiefe der Stichprobenkorrelation einer Stichprobe der Größe N aus einer bivariaten Normalverteilung mit echter Korrelation rho unter drei Bedingungen:
• rho = 0: Die Schiefe ist dann aus Symmetriegründen Null
• rho = 0,5: Bewerten Sie dies durch Simulation
• rho = 1 – epsilon: Finden Sie dies analytisch im Grenzfall heraus, bei dem sich epsilon 0 nähert.
Das ist nicht trivial, sollte aber auch nicht allzu schwer sein. Es sollte auch möglich sein, die asymptotische Schiefe der Verteilung im Grenzfall von großem N als niedrigdimensionales Integral auszudrücken, das dann numerisch ausgewertet werden kann – dies sollte stabiler sein als der Versuch, Dinge mithilfe von Brute-Pressure-Simulation zu berechnen. Außerdem können Sie innerhalb des Integralzeichens zweimal nach rho differenzieren und das Ergebnis mit Null vergleichen, was der Fall wäre, wenn die Funktion genau linear wäre. Was wiederum nicht der Fall ist – es scheint einfach, dass zu viele Dinge zusammenpassen müssten, damit dies klappt –, aber auch hier könnte meine Instinct falsch sein.
Additionally los, Wahrscheinlichkeits- und Statistikstudenten! Es ist ein kleines, klar definiertes Forschungsprojekt.
Und wenn Sie Fortschritte machen, teilen Sie uns dies bitte im Kommentarbereich mit.
PS Anscheinend handelt es sich hierbei nicht um ein Forschungsprojekt, da das Ergebnis bereits bekannt ist, zumindest wenn die zugrunde liegende Verteilung bivariat regular ist. Sehen dieser Kommentar unten.