dem k-NN-Regressor und der Idee der Vorhersage basierend auf der Distanz, schauen wir uns nun den k-NN-Klassifikator an.
Das Prinzip ist dasselbe, aber die Klassifizierung ermöglicht uns die Einführung mehrerer nützlicher Varianten, wie z. B. „Radius Nearest Neighbors“, „Nearest Centroid“, Multi-Class-Vorhersage und probabilistische Distanzmodelle.
Daher werden wir zunächst den k-NN-Klassifikator implementieren und dann diskutieren, wie er verbessert werden kann.
Sie können verwenden dieses Excel/Google-Blatt beim Lesen dieses Artikels, um allen Erklärungen besser folgen zu können.

Titanic-Überlebensdatensatz
Wir verwenden den Titanic-Überlebensdatensatz, ein klassisches Beispiel, bei dem jede Zeile einen Passagier mit Merkmalen wie Klasse, Geschlecht, Alter und Fahrpreis beschreibt und das Ziel darin besteht, vorherzusagen, ob der Passagier überlebt hat.

Prinzip von k-NN zur Klassifizierung
Der k-NN-Klassifikator ist dem k-NN-Regressor so ähnlich, dass ich quick einen einzigen Artikel schreiben könnte, um beide zu erklären.
Tatsächlich, wenn wir nach dem suchen ok Nächste Nachbarn, wir verwenden den Wert nicht j überhaupt, geschweige denn seine Natur.
ABER es gibt immer noch einige interessante Fakten darüber, wie Klassifikatoren (binär oder mehrklassig) erstellt werden und wie die Funktionen unterschiedlich gehandhabt werden können.
Wir beginnen mit der binären Klassifizierungsaufgabe und dann mit der Mehrklassenklassifizierung.
Ein kontinuierliches Merkmal für die binäre Klassifizierung
Mit diesem Datensatz können wir additionally ganz schnell die gleiche Übung für ein kontinuierliches Function durchführen.
Für den Wert von y verwenden wir normalerweise 0 und 1, um die beiden Klassen zu unterscheiden. Aber Sie können es bemerken, oder Sie werden bemerken, dass es Verwirrung stiften kann.

Denken Sie mal darüber nach: 0 und 1 sind auch Zahlen, oder? Wir können additionally genau den gleichen Prozess durchführen, als würden wir eine Regression durchführen.
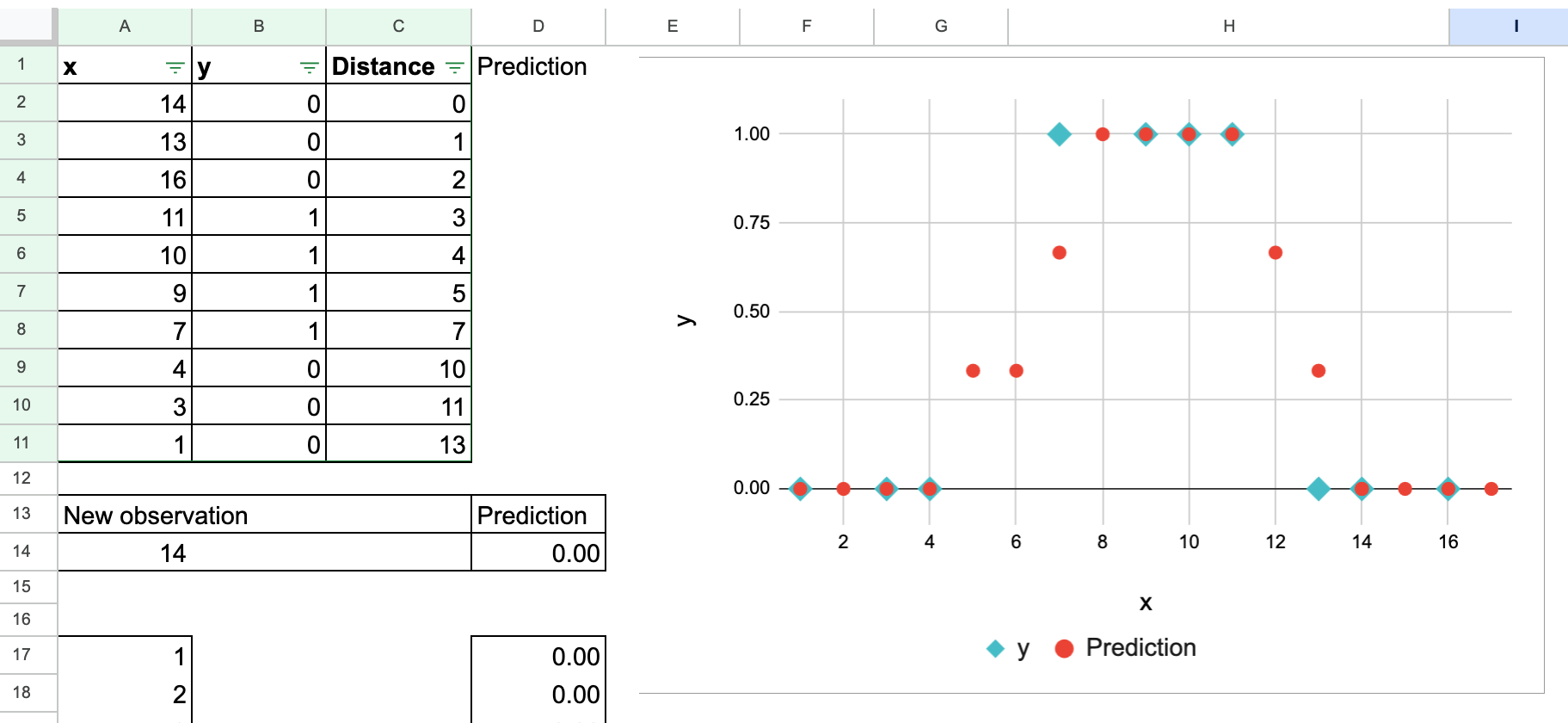
Das ist richtig. An der Berechnung ändert sich nichts, wie Sie im folgenden Screenshot sehen. Und Sie können natürlich versuchen, den Wert der neuen Beobachtung selbst zu ändern.

Der einzige Unterschied besteht darin, wie wir das Ergebnis interpretieren. Wenn wir den „Durchschnitt“ der Nachbarn nehmen j Werte, unter dieser Zahl versteht man die Wahrscheinlichkeit, dass die neue Beobachtung zur Klasse 1 gehört.
In Wirklichkeit ist der „durchschnittliche“ Wert additionally nicht die gute Interpretation, sondern vielmehr der Anteil der Klasse 1.
Wir können dieses Diagramm auch manuell erstellen, um zu zeigen, wie sich die vorhergesagte Wahrscheinlichkeit über einen Bereich von ändert X Werte.
Um zu vermeiden, dass die Wahrscheinlichkeit am Ende bei 50 Prozent liegt, wählen wir traditionell einen ungeraden Wert für okdamit wir immer mit Mehrheitsentscheidung entscheiden können.

Zwei Funktionen für die binäre Klassifizierung
Wenn wir zwei Merkmale haben, ist die Operation auch quick die gleiche wie beim k-NN-Regressor.

Eine Funktion für die Klassifizierung mehrerer Klassen
Nehmen wir nun ein Beispiel für drei Klassen für die Zielvariable y.
Dann sehen wir, dass wir den Begriff „Durchschnitt“ nicht mehr verwenden können, da die Zahl, die die Kategorie darstellt, eigentlich keine Zahl ist. Und wir sollten sie besser „Kategorie 0“, „Kategorie 1“ und „Kategorie 2“ nennen.

Von k-NN zu den nächstgelegenen Schwerpunkten
Wenn ok zu groß wird
Jetzt machen wir ok groß. Wie groß? So groß wie möglich.
Denken Sie daran, dass wir diese Übung auch mit dem k-NN-Regressor durchgeführt haben und die Schlussfolgerung lautete: Wenn ok der Gesamtzahl der Beobachtungen im Trainingsdatensatz entspricht, ist der k-NN-Regressor der einfache Durchschnittswertschätzer.
Für den k-NN-Klassifikator ist es quick dasselbe. Wenn ok der Gesamtzahl der Beobachtungen entspricht, erhalten wir für jede Klasse ihren Gesamtanteil im gesamten Trainingsdatensatz.
Manche Leute bezeichnen diese Proportionen aus bayesianischer Sicht als Priors!
Dies hilft uns jedoch nicht viel bei der Klassifizierung einer neuen Beobachtung, da diese Prioritäten für jeden Punkt gleich sind.
Die Schaffung von Schwerpunkten
Gehen wir additionally noch einen Schritt weiter.
Für jede Klasse können wir auch alle Merkmalswerte gruppieren X die zu dieser Klasse gehören, und berechnen Sie ihren Durchschnitt.
Diese gemittelten Merkmalsvektoren nennen wir Schwerpunkte.
Was können wir mit diesen Schwerpunkten machen?
Wir können sie verwenden, um eine neue Beobachtung zu klassifizieren.
Anstatt die Abstände zum gesamten Datensatz für jeden neuen Punkt neu zu berechnen, messen wir einfach den Abstand zu jedem Klassenschwerpunkt und weisen die Klasse des nächstgelegenen zu.
Mit dem Überlebensdatensatz der Titanic können wir mit einer einzigen Funktion beginnen: Alterund berechnen Sie die Schwerpunkte für die beiden Klassen: Passagiere, die überlebt haben, und Passagiere, die nicht überlebt haben.

Jetzt ist es auch möglich, mehrere kontinuierliche Funktionen zu verwenden.
Beispielsweise können wir die beiden Merkmale Alter und Fahrpreis nutzen.

Und wir können einige wichtige Merkmale dieses Modells diskutieren:
- Die Skala ist wichtig, wie wir bereits für den k-NN-Regressor besprochen haben.
- Die fehlenden Werte stellen hier kein Drawback dar: Wenn wir die Schwerpunkte professional Klasse berechnen, wird jeder einzelne mit den verfügbaren (nicht leeren) Werten berechnet
- Wir sind vom „komplexesten“ und „größten“ Modell (in dem Sinne, dass das eigentliche Modell der gesamte Trainingsdatensatz ist, sodass wir den gesamten Datensatz speichern müssen) zum einfachsten Modell übergegangen (wir verwenden nur einen Wert professional Function und speichern nur diese Werte als unser Modell).
Von stark nichtlinear bis naiv linear
Aber fällt Ihnen jetzt ein großer Nachteil ein?
Während der grundlegende k-NN-Klassifikator stark nichtlinear ist, ist die Nearest Centroid-Methode äußerst linear.
In diesem 1D-Beispiel sind die beiden Schwerpunkte einfach die durchschnittlichen x-Werte der Klassen 0 und 1. Da diese beiden Durchschnittswerte nahe beieinander liegen, wird die Entscheidungsgrenze lediglich zum Mittelpunkt zwischen ihnen.
Anstelle einer stückweisen, gezackten Grenze, die von der genauen Place vieler Trainingspunkte abhängt (wie in k-NN), erhalten wir additionally einen geraden Cutoff, der nur von zwei Zahlen abhängt.
Dies veranschaulicht, wie Nearest Centroids den gesamten Datensatz in eine einfache und sehr lineare Regel komprimiert.

Ein Hinweis zur Regression: Warum Schwerpunkte nicht gelten
Eine solche Verbesserung ist für den k-NN-Regressor nicht möglich. Warum?
Bei der Klassifizierung bildet jede Klasse eine Gruppe von Beobachtungen, sodass die Berechnung des durchschnittlichen Merkmalsvektors für jede Klasse sinnvoll ist und wir dadurch die Klassenschwerpunkte erhalten.
Aber in der Regression das Ziel j ist kontinuierlich. Es gibt keine diskreten Gruppen, keine Klassengrenzen und daher keine sinnvolle Möglichkeit, den „Schwerpunkt einer Klasse“ zu berechnen.
Ein kontinuierliches Ziel hat unendlich viele mögliche Werte, daher können wir Beobachtungen nicht nach ihnen gruppieren j Wert, um Schwerpunkte zu bilden.
Der einzig mögliche „Schwerpunkt“ in der Regression wäre der globaler Mittelwertwas dem Fall ok = N im k-NN-Regressor entspricht.
Und dieser Schätzer ist viel zu einfach, um nützlich zu sein.
Kurz gesagt, der Nearest Centroids Classifier ist eine natürliche Verbesserung der Klassifizierung, hat aber kein direktes Äquivalent in der Regression.
Weitere statistische Verbesserungen
Was können wir sonst noch mit dem grundlegenden k-NN-Klassifikator machen?
Durchschnitt und Varianz
Mit dem Nearest Centroids Classifier haben wir die einfachste Statistik verwendet Durchschnitt. Ein natürlicher Reflex in der Statistik besteht darin, das zu addieren Varianz sowie.
Nun ist der Abstand additionally nicht mehr euklidisch, sondern Mahalanobis Distanz. Mithilfe dieser Distanz erhalten wir die Wahrscheinlichkeit basierend auf der Verteilung, die durch den Mittelwert und die Varianz jeder Klasse gekennzeichnet ist.
Umgang mit kategorialen Options
Für kategoriale Merkmale können wir keine Durchschnittswerte oder Varianzen berechnen. Und für den k-NN-Regressor haben wir gesehen, dass es möglich ist, eine One-Sizzling-Codierung oder eine Ordinal-/Label-Codierung durchzuführen. Aber der Maßstab ist wichtig und nicht leicht zu bestimmen.
Hier können wir im Hinblick auf die Wahrscheinlichkeiten etwas ebenso Bedeutsames tun: Wir können Zählen Sie die Anteile jeder Kategorie innerhalb einer Klasse.
Diese Proportionen verhalten sich genau wie Wahrscheinlichkeiten und beschreiben, wie wahrscheinlich jede Kategorie innerhalb jeder Klasse ist.
Diese Idee steht in direktem Zusammenhang mit Modellen wie Kategorischer naiver Bayeswobei Klassen gekennzeichnet sind durch Häufigkeitsverteilungen über die Kategorien.
Gewichtete Distanz
Eine andere Richtung besteht darin, Gewichte einzuführen, sodass nähere Nachbarn mehr zählen als entfernte. In scikit-learn gibt es das Argument „Gewichte“, das uns dies ermöglicht.
Wir können auch von „ok Nachbarn“ zu einem festen Radius um die neue Beobachtung wechseln, was zu radiusbasierten Klassifikatoren führt.
Radius Nächste Nachbarn
Manchmal können wir die folgende Grafik finden, um den k-NN-Klassifikator zu erklären. Aber tatsächlich spiegelt ein solcher Radius eher die Idee des „Radius der nächsten Nachbarn“ wider.
Ein Vorteil ist die Kontrolle der Nachbarschaft. Besonders interessant ist es, wenn wir die konkrete Bedeutung der Entfernung kennen, beispielsweise die geografische Entfernung.

Der Nachteil ist jedoch, dass Sie den Radius im Voraus kennen müssen.
Übrigens eignet sich dieser Begriff des Radius nächster Nachbarn auch für die Regression.
Zusammenfassung verschiedener Varianten
All diese kleinen Änderungen führen zu unterschiedlichen Modellen, von denen jedes versucht, die Grundidee des Vergleichs von Nachbarn anhand einer komplexeren Definition der Entfernung mit einem Kontrollparameter zu verbessern, der es uns ermöglicht, lokale Nachbarn oder eine globalere Charakterisierung der Nachbarschaft zu erhalten.
Wir werden hier nicht alle diese Modelle untersuchen. Ich kann einfach nicht anders, als etwas zu weit zu gehen, wenn eine kleine Variation natürlich zu einer anderen Idee führt.
Betrachten Sie dies vorerst als Ankündigung der Modelle, die wir später in diesem Monat implementieren werden.

Abschluss
In diesem Artikel haben wir den k-NN-Klassifikator von seiner grundlegendsten Kind bis hin zu mehreren Erweiterungen untersucht.
An der Grundidee ändert sich nichts: Eine neue Beobachtung wird anhand der Ähnlichkeit mit den Trainingsdaten klassifiziert.
Aber diese einfache Idee kann viele verschiedene Formen annehmen.
Bei kontinuierlichen Merkmalen basiert die Ähnlichkeit auf dem geometrischen Abstand.
Bei kategorialen Merkmalen betrachten wir stattdessen, wie oft jede Kategorie unter den Nachbarn vorkommt.
Wenn ok sehr groß wird, zerfällt der gesamte Datensatz in nur wenige zusammenfassende Statistiken, was natürlich dazu führt Klassifikator für nächstgelegene Schwerpunkte.
Das Verständnis dieser Familie distanzbasierter und wahrscheinlichkeitsbasierter Ideen hilft uns zu erkennen, dass viele Modelle des maschinellen Lernens einfach unterschiedliche Möglichkeiten zur Beantwortung derselben Frage darstellen:
Welcher Klasse ähnelt diese neue Beobachtung am meisten?
In den nächsten Artikeln werden wir uns weiterhin mit dichtebasierten Modellen befassen, die als globale Maße für die Ähnlichkeit zwischen Beobachtungen und Klassen verstanden werden können.