In meinem vorherige Beiträge in der Serie „Zeitreihen für Scikit-Be taught-Leute“ habe ich besprochen, wie man ein maschinelles Lernmodell trainieren kann, um vorhersagen das nächste Component in einer Zeitreihe. Oft möchte man den Wert der Zeitreihe für die Zukunft vorhersagen. In diesen Beiträgen habe ich zwei Methoden beschrieben, um dies zu erreichen. Eine Methode besteht darin, das maschinelle Lernmodell so zu trainieren, dass es speziell diesen Zeitpunkt in der Zukunft vorhersagt. Diese Methode ist schlecht, denn wenn man den Wert der Zeitreihe zu zwei verschiedenen Zeitpunkten in der Zukunft wissen möchte, hat man wieder Pech.
Die andere Methode ist die rekursive Prognose. Dies wird erreicht, indem die Vorhersage des Modells als neuer Enter eingespeist wird und dieser zur Vorhersage eines neuen Outputs verwendet wird. Dies wird iteriert, indem die Vorhersagen „weitergerollt“ werden, bis der zukünftige interessierende Punkt erreicht ist. In Python würde dies folgendermaßen aussehen:
def recursive_forecast(mannequin, input_data, num_points_in_future):
for level in vary(num_points_in_future):
prediction = mannequin.predict(input_data)
# Append prediction to the enter knowledge
input_data = np.hstack((input_data, prediction))
return prediction
Aus der Sicht des maschinellen Lernens ist diese Type der Prognose bizarr. Sie könnten ein Modell trainieren, das einen hervorragenden Testfehler bei der Vorhersage des nächsten Schritts in einer Zeitreihe aufweist, dann aber bei der Vorhersage mehrerer Werte in der Zeitreihe spektakulär versagt. Wenn Ihr wahres Ziel darin besteht, den Fehler bei der Vorhersage mehrerer zukünftiger Werte in einer Zeitreihe zu minimieren, dann sollten Sie eine Verlustfunktion konstruieren, die diesen Fehler direkt minimiert! In diesem Blogbeitrag zeige ich Ihnen ein paar verschiedene Möglichkeiten, diese sogenannte direkte Prognose mithilfe meiner Bibliothek durchzuführen. Sketche. Unterwegs werden wir Spaß daran haben, die Kette der Modellkomplexität hinaufzusteigen, von scikit-learn lineare Modelle, um XGBoostzu Deep-Studying-Modellen in PyTorch. Und natürlich wird alles kompatibel sein mit dem scikit-learn API.
Hinweis: Obwohl rekursive Prognosen aus der Sicht des maschinellen Lernens verrückt erscheinen, gibt es viele gute Gründe, sie zu verwenden. Zudem ist die Frage, ob rekursive oder direkte Prognosen verwendet werden sollen, recht differenziert. Souhaib Ben Taiebs Doktorarbeit Dissertation (pdf) hat eine gute Diskussion mit Referenzen.
Im Zweifelsfall mehrere Modelle verwenden
Wenn Rechenleistung, Speicher und Zeit günstig sind, können Sie eine Prognose mit roher Gewalt erstellen, indem Sie für jeden Zeitpunkt in der Zukunft, den Sie vorhersagen möchten, ein separates Modell trainieren. Wenn Sie beispielsweise eine Zeitreihe mit einer Stichprobe professional Minute haben (d. h. eine Stichprobenfrequenz von 1/60 Hz) und jeden Zeitpunkt in der nächsten Stunde vorhersagen möchten, würden Sie 60 verschiedene Modelle trainieren. Jedes Modell hätte einen anderen Zeitpunkt in der Zukunft als „Ziel“ (oder y In scikit-learn Umgangssprache), und Sie würden eine Vorhersage für die volle Stunde erstellen, indem Sie die Vorhersage jedes Modells berechnen.
Das Schöne an dieser Methode ist, dass Sie jedes beliebige Regressionsmodell verwenden können, das ein einzelnes Ziel vorhersagt. Und tatsächlich stellt sich heraus, dass scikit-learn hat eine Klasse, die Ihnen dies ermöglicht. Alles, was Sie tun müssen, ist, Ihren Modellschätzer mit dem MultiOutputRegressor Klasse. Einmal eingewickelt, dann scikit-learn trainiert einen individuellen Schätzer für jede Spalte in Ihrem y Matrix. Wir müssen additionally nur unsere Zeitreihe transformieren y so dass es sich von einem Array in eine Matrix verwandelt, in der jede Spalte einen Schritt in die Zukunft darstellt. Die HorizonTransformer In skits tut genau dies. Für eine horizon von 3geht eine Zeitreihe von
import numpy as np
y = np.arange(10, dtype=np.float32)
y
array((0., 1., 2., 3., 4., 5., 6., 7., 8., 9.), dtype=float32)
from skits.preprocessing import HorizonTransformer
ht = HorizonTransformer(horizon=3)
y_horizon = ht.fit_transform(y.reshape(-1, 1))
y_horizon
array((( 0., 1., 2.),
( 1., 2., 3.),
( 2., 3., 4.),
( 3., 4., 5.),
( 4., 5., 6.),
( 5., 6., 7.),
( 6., 7., 8.),
(nan, nan, nan),
(nan, nan, nan),
(nan, nan, nan)), dtype=float32)
Notiere dass der HorizonTransformer behält die Länge der y Array, additionally erhalten wir NaN Werte für die letzten 3 Zeilen.
Einfach anfangen: Lineare Modelle
Versuchen wir nun, ein lineares Regressionsmodell zu trainieren, um die Daten der nächsten zwei Stunden in unserem guten alten Citibike-Datensatz vorherzusagen, den ich in dieser Serie verwendet habe. Abrufen dass die Daten aus der Anzahl der Fahrräder bestehen, die an der Citibike-Station in der Nähe meiner Wohnung verfügbar waren. Die Punkte in der Zeitreihe sind 5 Minuten voneinander entfernt. Wenn wir additionally die nächsten 2 Stunden Daten vorhersagen möchten, müssen wir die nächsten 24 Punkte in der Zeitreihe vorhersagen.
%config InlineBackend.figure_format = 'retina'
import matplotlib as mpl
import matplotlib.pyplot as plt
plt.ion()
mpl.rcParams('determine.figsize') = (10, 6)
mpl.rcParams('determine.titlesize') = 16
mpl.rcParams('axes.labelsize') = 14
mpl.rcParams('axes.titlesize') = 16
mpl.rcParams('legend.fontsize') = 14
mpl.rcParams('xtick.labelsize') = 12
mpl.rcParams('ytick.labelsize') = 12
import pickle
with open('station_496_availability.pkl', 'rb') as f:
y = pickle.load(f)
plt.plot(y(:2500));
plt.xlabel('Time Index');
plt.ylabel('Variety of Bikes');
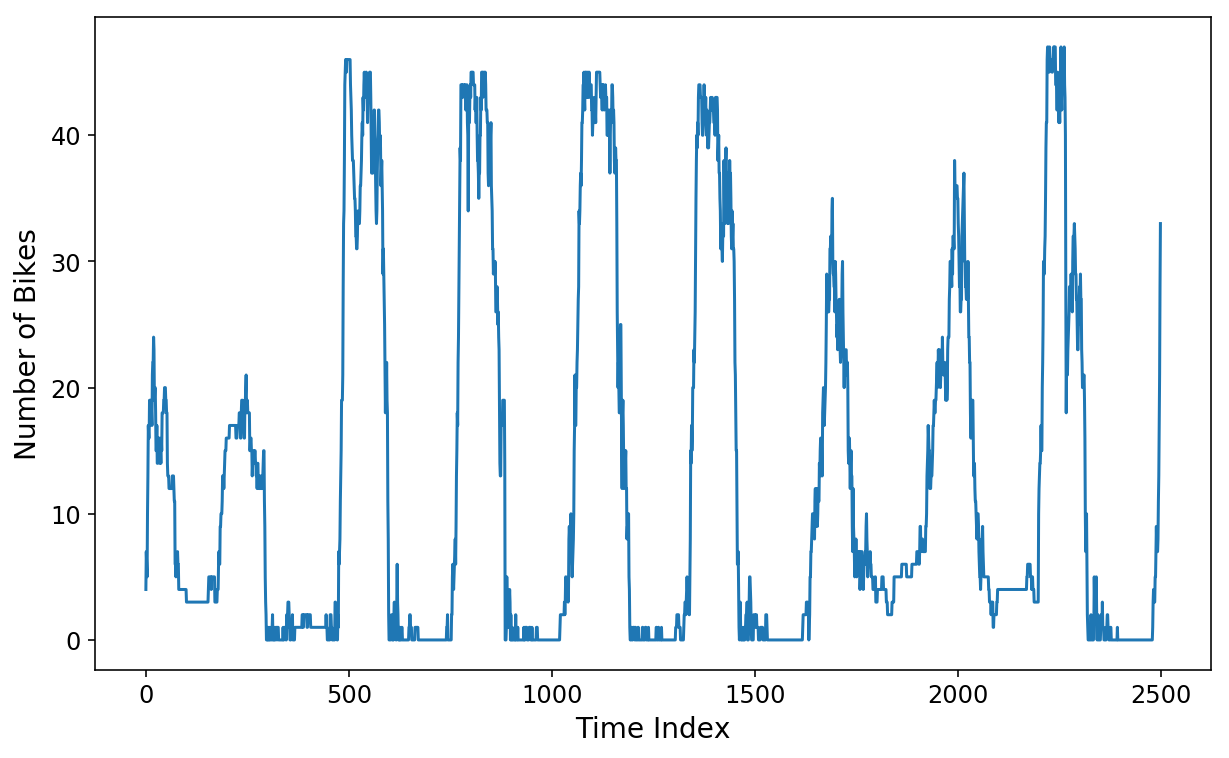
Wir verwenden skits eine Designmatrix zu konstruieren, die aus den vorherigen Wochen Daten im Wert. Das ist definitiv übertrieben, aber ich möchte viele Funktionen in die komplexeren Modelle einbauen, die wir später erstellen werden.
period_minutes = 5
samples_per_hour = int(60 / period_minutes)
samples_per_day = int(24 * samples_per_hour)
samples_per_week = int(7 * samples_per_day)
print(f'Variety of "options": {samples_per_week}')
Variety of "options": 2016
from sklearn.linear_model import LinearRegression
from sklearn.multioutput import MultiOutputRegressor
from sklearn.pipeline import FeatureUnion
from skits.feature_extraction import AutoregressiveTransformer
from skits.pipeline import ForecasterPipeline
from skits.preprocessing import ReversibleImputer
lin_pipeline = ForecasterPipeline((
# Convert the `y` goal right into a horizon
('pre_horizon', HorizonTransformer(horizon=samples_per_hour * 2)),
('pre_reversible_imputer', ReversibleImputer(y_only=True)),
('options', FeatureUnion((
# Generate every week's value of autoregressive options
('ar_features', AutoregressiveTransformer(num_lags=samples_per_week)),
))),
('post_feature_imputer', ReversibleImputer()),
('regressor', MultiOutputRegressor(LinearRegression(fit_intercept=False),
n_jobs=6))
))
Wir haben jetzt eine pipeline das eine Woche lang autoregressive Merkmale generiert und eine LinearRegression Modell für jeden der 24 Punkte im 2-Stunden-Horizont, den wir vorhersagen möchten. Wir reservieren 1000 Punkte am Ende der Zeitreihe als unsere „Testdaten“, obwohl dies kein echtes Coaching/Take a look at/Kreuzvalidierungsverfahren darstellen soll.
X = y.reshape(-1, 1).copy()
test_size = 1000
train_size = len(X) - test_size
lin_pipeline = lin_pipeline.match(X(:train_size), y(:train_size))
Vorhersageinspektion
Mit der angepassten Pipeline können wir nun Horizontvorhersagen generieren. predict auf der Pipeline wird nun eine 2-stündige, 24 Datenpunktvorhersage an jedem Punkt in den Daten generiert X. Vorbeigehen start_idx gibt Vorhersagen zurück, beginnend bei start_idx von X (was in unserem Fall der Anfang der Testdaten sein wird).
prediction hat 24 Spalten, wobei die erste Spalte den ersten Datenpunkt in der Zukunft (in unserem Fall 5 Minuten in der Zukunft) bis hinauf zum 24. Datenpunkt in der Zukunft darstellt.
lin_prediction = lin_pipeline.predict(X, start_idx=train_size)
print(f'X form: {X.form}')
print(f'prediction form: {lin_prediction.form}')
X form: (74389, 1)
prediction form: (1000, 24)
Es gibt verschiedene Möglichkeiten, wie wir unsere Vorhersage überprüfen können. Zunächst können wir eine einzelne 2-Stunden-Vorhersage mit den Floor-Fact-Testdaten vergleichen.
plt.determine();
plt.plot(y(-test_size:), 'okay.-');
plt.plot(np.arange(350, 374), lin_prediction(350, :), linewidth=6);
plt.ylabel('Variety of Bikes Obtainable');
plt.xlabel('Time Index');
plt.title('Autoregressive Linear Mannequin');
plt.legend(('Precise Bike Availability',
'Predicted availability nat Time Index 350'));
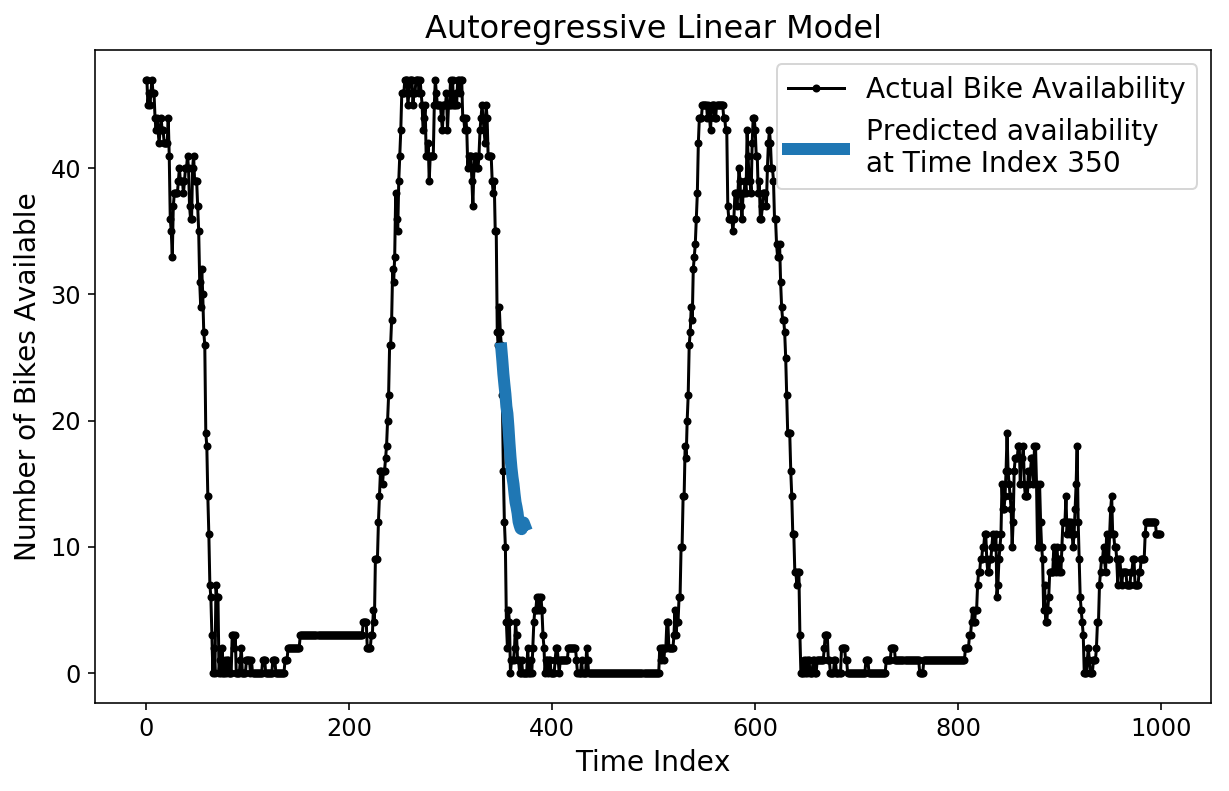
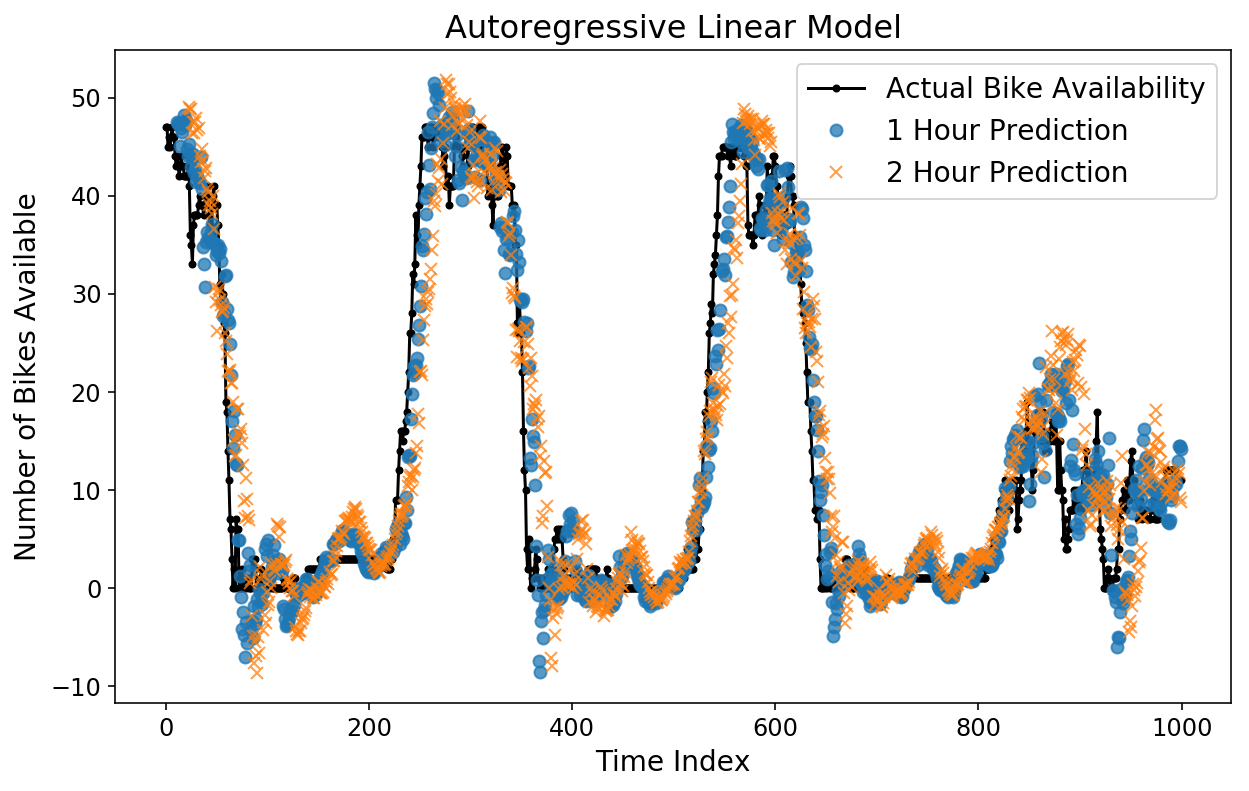
Wir können auch verschiedene Horizontvorhersagen übereinanderlegen, um sie im Vergleich zueinander zu vergleichen. Unten stelle ich die tatsächliche Fahrradverfügbarkeit, die 1-Stunden-Vorhersage und die 2-Stunden-Vorhersage dar. Die 1-Stunden-Vorhersage entspricht dem, was unser Modell für die Fahrradverfügbarkeit zu einem bestimmten Zeitpunkt vorhersagen würde, wenn alle Daten bis zu einer Stunde vor diesem Zeitpunkt vorliegen.
Überraschenderweise sehen sowohl die 1-Stunden- als auch die 2-Stunden-Vorhersagen optisch ziemlich intestine aus! Sie können sehen, dass die 2-Stunden-Vorhersage im Vergleich zur 1-Stunden-Vorhersage etwas stärker von den tatsächlichen Daten abweicht, was Sinn macht.
plt.determine();
plt.plot(y(-test_size:), 'okay.-');
plt.plot(np.arange(11, test_size), lin_prediction(:-11, 11), 'o', alpha=0.75);
plt.plot(np.arange(23, test_size), lin_prediction(:-23, 23), 'x', alpha=0.75);
plt.legend(('Precise Bike Availability',
'1 Hour Prediction',
'2 Hour Prediction'));
plt.ylabel('Variety of Bikes Obtainable');
plt.xlabel('Time Index');
plt.title('Autoregressive Linear Mannequin');
Das Betrachten von Diagrammen ist hilfreich für die Instinct, aber nicht besonders streng, wenn es um die Bewertung der tatsächlichen Leistung geht. Wir können eine einfache Leistungsmetrik verwenden und den mittleren absoluten Fehler (MAE) als Funktion jedes Zeitpunkts in der Zukunft berechnen, den wir schätzen möchten. Glücklicherweise scikit-learn verfügt über integrierte Funktionen, die dies für 2D handhaben y Daten.
Warum eigentlich absoluten Fehler meinen? Bei etwas wie der Fahrradverfügbarkeit ist es ganz natürlich, die Frage beantworten zu wollen: „Wie viele Fahrräder fehlen uns möglicherweise, wenn wir die Fahrradverfügbarkeit in einer Stunde vorhersagen?“
from sklearn.metrics import mean_absolute_error
y_actual = lin_pipeline.transform_y(X)
lin_mae = mean_absolute_error(y_actual(-test_size:), lin_prediction,
multioutput='raw_values')
plt.plot(np.arange(1, 25) * 5, lin_mae);
plt.xlabel('Minutes within the Future');
plt.ylabel('Imply Absolute Error');
plt.title('Autoregressive Linear Mannequin MAE');
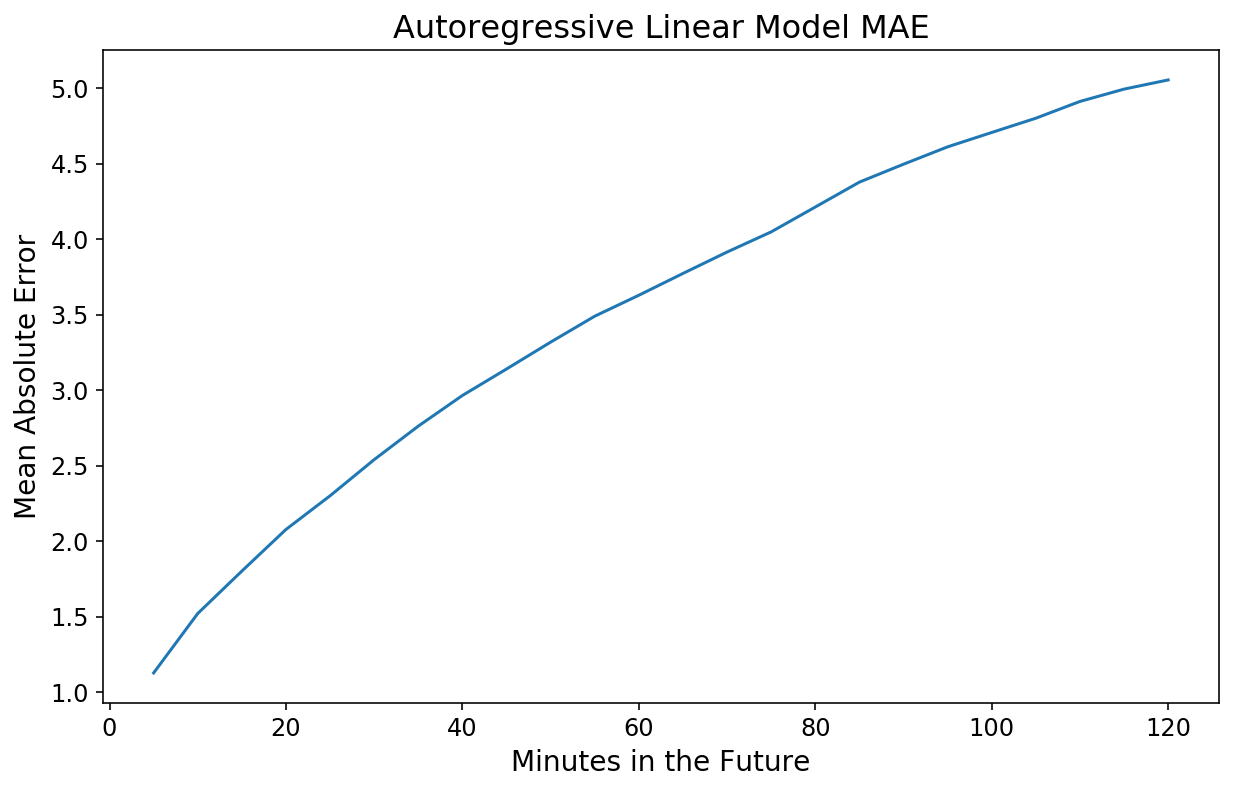
Nicht schlecht! Unsere 20-Minuten-Vorhersage weicht im Durchschnitt um 2 Fahrräder ab, und unsere 2-Stunden-Vorhersage weicht nur um 5 Fahrräder ab.
Obwohl unsere Horizontvorhersage ziemlich intestine aussieht, können wir immer noch eine rekursive Vorhersage ausprobieren, indem wir den pipeline.forecast Methode. Wir generieren eine rekursive Prognose, beginnend bei Index 530 in den Testdaten.
forecast = lin_pipeline.forecast(X,
start_idx=train_size + 530,
trans_window=samples_per_week)
plt.plot(y(-test_size+500:-test_size + 560), 'okay.-');
plt.plot(forecast(-test_size+500:-test_size + 560, 0), '-.');
plt.plot((30, 30), (0, 45));
plt.legend(('Precise Bike Availability',
'Recursive Forecast',
'Forecasting Begin'));
plt.ylabel('Bike Availability');
plt.xlabel('Time Index');
plt.title('Recursive Forecast Comparability');
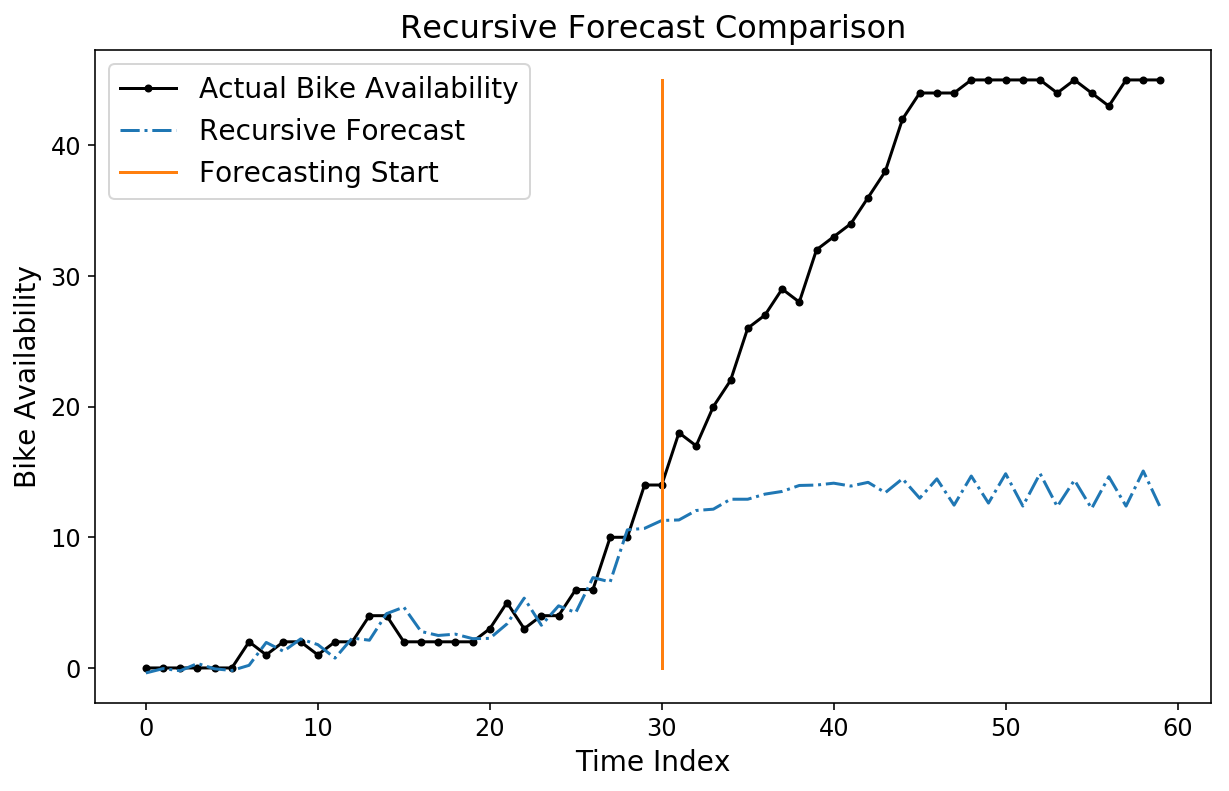
Beachten Sie, dass unsere Prognose ziemlich schlecht aussieht! Um ehrlich zu sein, ist es nicht unbedingt klar, dass wir sollen eine gute Prognose haben, da das Modell darauf trainiert wurde, Horizontprognosen zu optimieren und nicht rekursive Prognosen.
Booster
Nur weil wir es können, versuchen wir, für unsere Horizontvorhersagen ein XGBoost-Modell zu trainieren, statt einer linearen Regression. Ich glaube nicht, dass es möglich ist, ein Multioutput-Regressionsziel mit XGBoost direkt zu optimieren, additionally werden wir den gleichen Weg wie beim linearen Modell gehen und 24 verschiedene XGBoost-Schätzer trainieren.
from xgboost import XGBRegressor
xgb_pipeline = ForecasterPipeline((
# Convert the `y` goal right into a horizon
('pre_horizon', HorizonTransformer(horizon=samples_per_hour * 2)),
('pre_reversible_imputer', ReversibleImputer(y_only=True)),
('options', FeatureUnion((
# Generate every week's value of autoregressive options
('ar_features', AutoregressiveTransformer(num_lags=samples_per_week)),
))),
('post_feature_imputer', ReversibleImputer()),
('regressor', MultiOutputRegressor(XGBRegressor(n_jobs=12,
n_estimators=300)))
))
xgb_pipeline = xgb_pipeline.match(X(:train_size), y(:train_size))
xgb_prediction = xgb_pipeline.predict(X, start_idx=train_size)
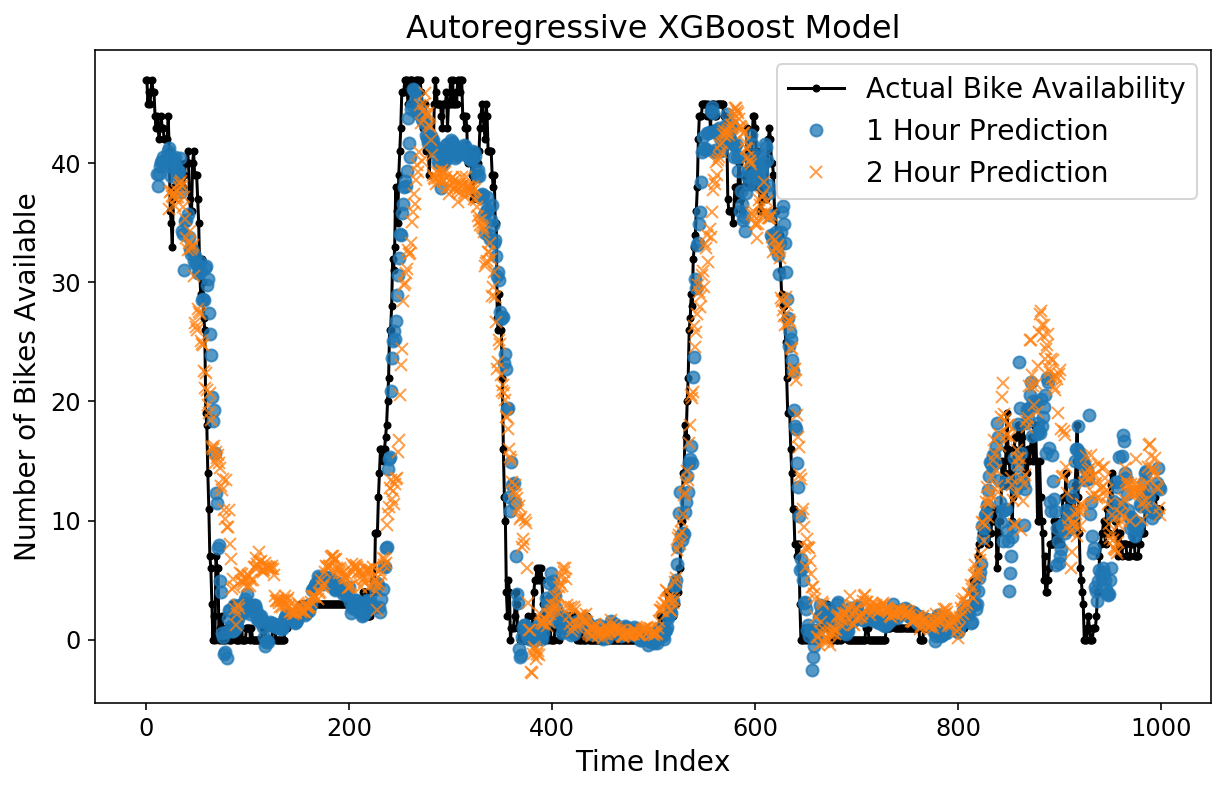
Schauen wir uns die Horizontvorhersagen an. Auf den ersten Blick sieht es besser aus als beim linearen Modell, und das MAE-Diagramm bestätigt dies.
plt.determine();
plt.plot(y(-test_size:), 'okay.-');
plt.plot(np.arange(11, test_size), xgb_prediction(:-11, 11), 'o', alpha=0.75);
plt.plot(np.arange(23, test_size), xgb_prediction(:-23, 23), 'x', alpha=0.75);
plt.legend(('Precise Bike Availability',
'1 Hour Prediction',
'2 Hour Prediction'));
plt.ylabel('Variety of Bikes Obtainable');
plt.xlabel('Time Index');
plt.title('Autoregressive XGBoost Mannequin');
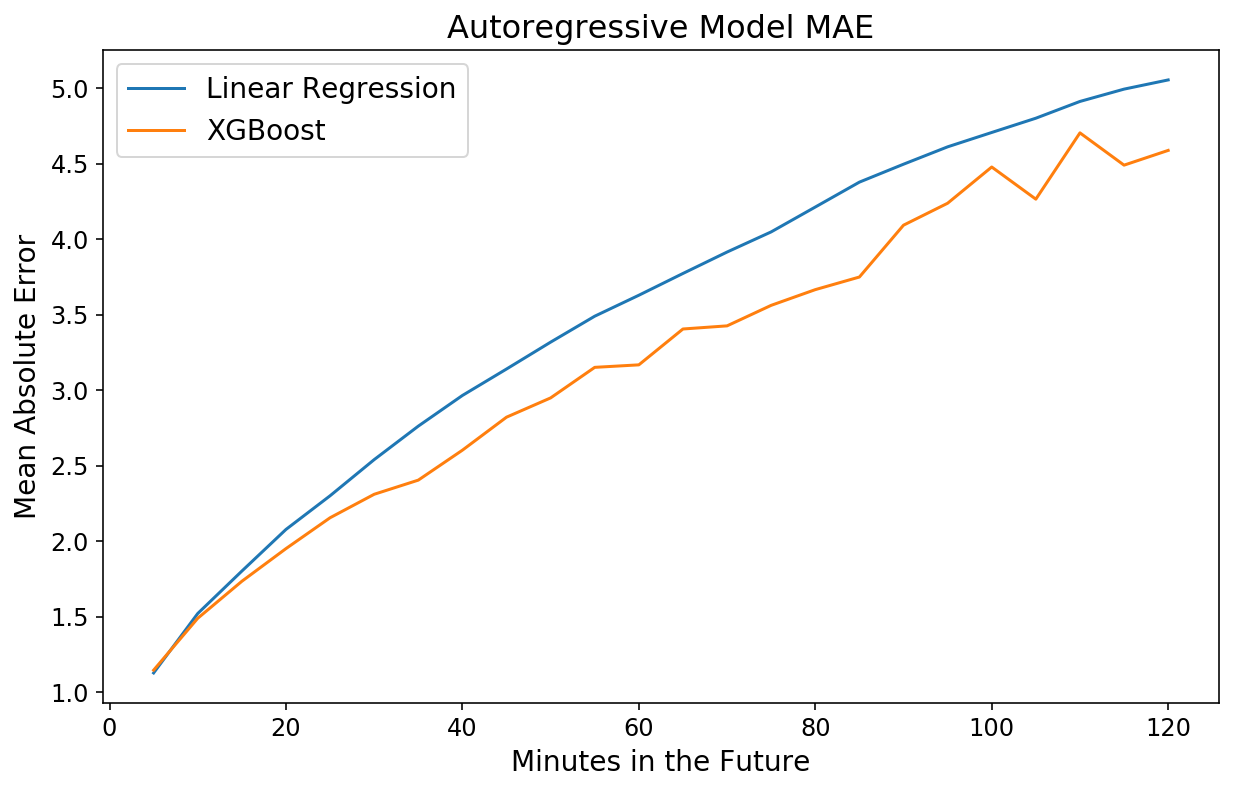
y_actual = xgb_pipeline.transform_y(X)
xgb_mae = mean_absolute_error(y_actual(-test_size:), xgb_prediction,
multioutput='raw_values')
plt.plot(np.arange(1, 25) * 5, lin_mae);
plt.plot(np.arange(1, 25) * 5, xgb_mae);
plt.xlabel('Minutes within the Future');
plt.ylabel('Imply Absolute Error');
plt.title('Autoregressive Mannequin MAE');
plt.legend(('Linear Regression', 'XGBoost'));
Tief drinnen
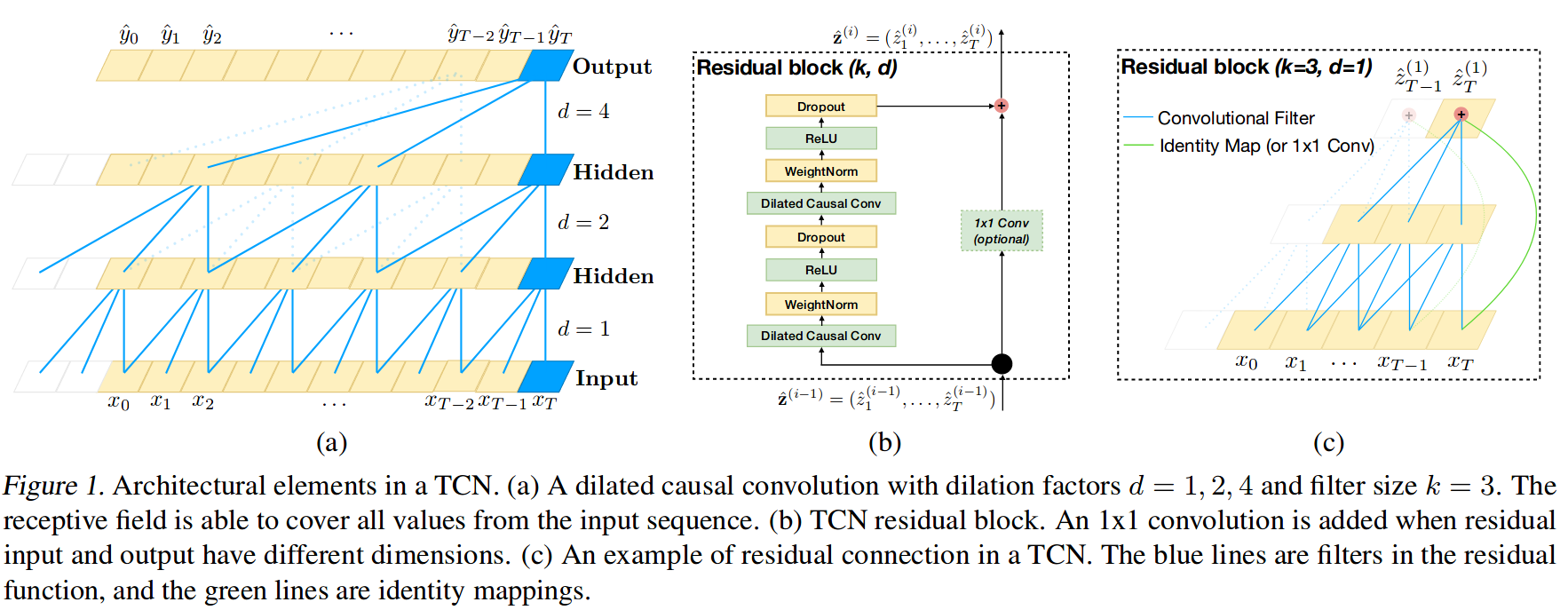
Zum Schluss trainieren wir noch ein Deep-Studying-Modell für die Horizontvorhersage. Ich habe schon einmal darüber geschrieben, wie sehr ich die verbrennen Bibliothek, und wir werden sie hier erneut verwenden. Mit skorch können wir jedes PyTorch-Modell in einen Scikit-Be taught-Schätzer umwandeln. Ich habe kurz nach den neuesten und besten Möglichkeiten zur Sequenzmodellierung mit Deep Studying gegoogelt und bin auf Folgendes gestoßen Papier das argumentiert, dass die Verwendung von Convolutional Neural Networks für Sequenzen tatsächlich besser und effizienter ist als rekurrierende Architekturen. Die Autoren waren so freundlich, eine PyTorch-Implementierung ihrer Code als Ergänzung zu dem Dokument, daher werde ich ihren Code unten zur Erstellung von „Temproal Convolutional Networks“ (TCN) wiederverwenden.
Um es klarzustellen: Ich verstehe wahrscheinlich 75 % des Papiers. Unten sehen Sie ein Diagramm (Abbildung 1 aus dem Papier) des TCN. Ich würde empfehlen, das Papier zu lesen, wenn Sie besonders interessiert sind.
from sklearn.preprocessing import StandardScaler
from skorch.regressor import NeuralNetRegressor
from skorch.callbacks import GradientNormClipping
import torch
from torch import nn
import torch.nn.practical as F
from torch.nn.utils import weight_norm
"""
Beneath code on this cell is taken from
https://github.com/locuslab/TCN
"""
class Chomp1d(nn.Module):
def __init__(self, chomp_size):
tremendous(Chomp1d, self).__init__()
self.chomp_size = chomp_size
def ahead(self, x):
return x(:, :, :-self.chomp_size).contiguous()
class TemporalBlock(nn.Module):
def __init__(self, n_inputs, n_outputs, kernel_size, stride, dilation, padding, dropout=0.2):
tremendous(TemporalBlock, self).__init__()
self.conv1 = weight_norm(nn.Conv1d(n_inputs, n_outputs, kernel_size,
stride=stride, padding=padding, dilation=dilation))
self.chomp1 = Chomp1d(padding)
self.relu1 = nn.ReLU()
self.dropout1 = nn.Dropout(dropout)
self.conv2 = weight_norm(nn.Conv1d(n_outputs, n_outputs, kernel_size,
stride=stride, padding=padding, dilation=dilation))
self.chomp2 = Chomp1d(padding)
self.relu2 = nn.ReLU()
self.dropout2 = nn.Dropout(dropout)
self.internet = nn.Sequential(self.conv1, self.chomp1, self.relu1, self.dropout1,
self.conv2, self.chomp2, self.relu2, self.dropout2)
self.downsample = nn.Conv1d(n_inputs, n_outputs, 1) if n_inputs != n_outputs else None
self.relu = nn.ReLU()
self.init_weights()
def init_weights(self):
self.conv1.weight.knowledge.normal_(0, 0.01)
self.conv2.weight.knowledge.normal_(0, 0.01)
if self.downsample is not None:
self.downsample.weight.knowledge.normal_(0, 0.01)
def ahead(self, x):
out = self.internet(x)
res = x if self.downsample is None else self.downsample(x)
return self.relu(out + res)
class TemporalConvNet(nn.Module):
def __init__(self, num_inputs, num_channels, output_sz,
kernel_size=2, dropout=0.2):
tremendous(TemporalConvNet, self).__init__()
layers = ()
num_levels = len(num_channels)
for i in vary(num_levels):
dilation_size = 2 ** i
in_channels = num_inputs if i == 0 else num_channels(i-1)
out_channels = num_channels(i)
layers += (TemporalBlock(in_channels, out_channels, kernel_size, stride=1,
dilation=dilation_size,
padding=(kernel_size-1) * dilation_size,
dropout=dropout))
self.community = nn.Sequential(*layers)
self.linear = nn.Linear(num_channels(-1), output_sz)
self.last_activation = nn.ReLU()
self.output_sz = output_sz
def ahead(self, x):
batch_sz = x.form(0)
out = self.community(x.unsqueeze(1))
out = out.transpose(1, 2)
out = self.linear(out).imply(dim=1)
return out
Das Dokument erwähnt die Verwendung von Standardeinstellungen von 0,002 Lernrate, Gradientennorm-Clipping und die Sicherstellung, dass die Anzahl der Kanäle den gesamten Verlauf der Zeitreihe erfasst. Ich implementiere das alles unten und trainiere für 60 Epochen. Beachten Sie, dass wir in diesem Fall nicht 24 verschiedene Modelle trainieren müssen. Stattdessen ist unsere Verlustfunktion einfach der mittlere quadratische Fehler über den gesamten Horizont, und PyTorch kann automatisch Gradienten berechnen, um ein einzel Modell zur Optimierung für den gesamten Horizont.
internet = NeuralNetRegressor(
module=TemporalConvNet,
module__num_inputs=1,
module__num_channels=(10) * 11,
module__output_sz=2 * samples_per_hour,
module__kernel_size=5,
module__dropout=0.0,
max_epochs=60,
batch_size=256,
lr=2e-3,
optimizer=torch.optim.Adam,
system='cuda',
iterator_train__shuffle=True,
callbacks=(GradientNormClipping(gradient_clip_value=1,
gradient_clip_norm_type=2)),
train_split=None,
)
dl_pipeline = ForecasterPipeline((
('pre_scaler', StandardScaler()),
('pre_horizon', HorizonTransformer(horizon=samples_per_hour * 2)),
('pre_reversible_imputer', ReversibleImputer(y_only=True)),
('options', FeatureUnion((
('ar_features', AutoregressiveTransformer(num_lags=samples_per_week)),
))),
('post_feature_imputer', ReversibleImputer()),
('regressor', internet)
))
dl_pipeline = dl_pipeline.match(X(:train_size).astype(np.float32),
y(:train_size).astype(np.float32),
end_idx=-5)
dl_prediction = dl_pipeline.predict(X.astype(np.float32), start_idx=train_size,
to_scale=True)
plt.determine();
plt.plot(y(-test_size:), 'okay.-');
plt.plot(np.arange(11, test_size), dl_prediction(:-11, 11), 'o', alpha=0.75);
plt.plot(np.arange(23, test_size), dl_prediction(:-23, 23), 'x', alpha=0.75);
plt.legend(('Precise Bike Availability',
'1 Hour Prediction',
'2 Hour Prediction'));
plt.ylabel('Variety of Bikes Obtainable');
plt.xlabel('Time Index');
plt.title('Autoregressive Deep Studying Mannequin');
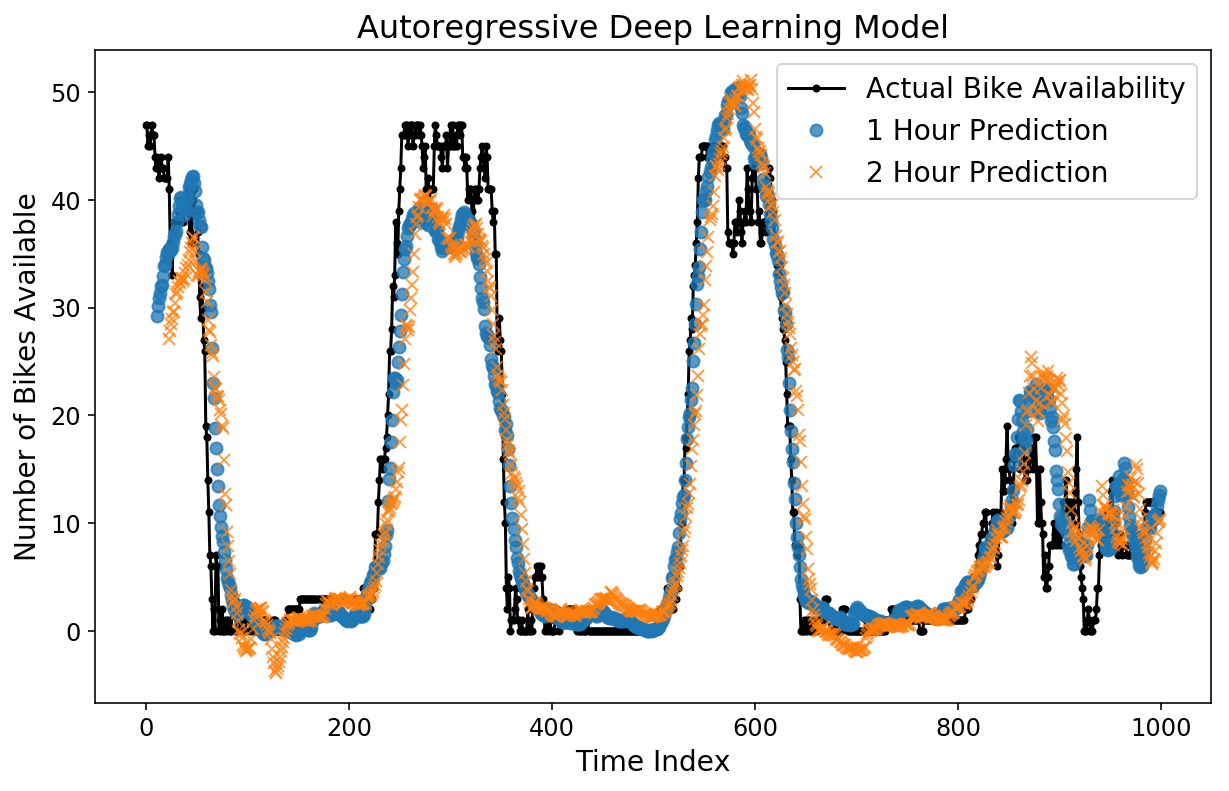
Die Vorhersagen sehen auf den ersten Blick ganz passabel aus. Schauen wir uns den MAE an.
y_actual = dl_pipeline.transform_y(X)
dl_mae = mean_absolute_error(y_actual(-test_size:),
dl_prediction,
multioutput='raw_values')
y_actual = dl_pipeline.transform_y(X)
dl_mae = mean_absolute_error(y_actual(-test_size:), dl_prediction,
multioutput='raw_values')
plt.plot(np.arange(1, 25) * 5, lin_mae);
plt.plot(np.arange(1, 25) * 5, xgb_mae);
plt.plot(np.arange(1, 25) * 5, dl_mae(:24))
plt.xlabel('Minutes within the Future');
plt.ylabel('Imply Absolute Error');
plt.title('Autoregressive Mannequin MAE');
plt.legend(('Linear Regression',
'XGBoost',
'Deep Studying'));
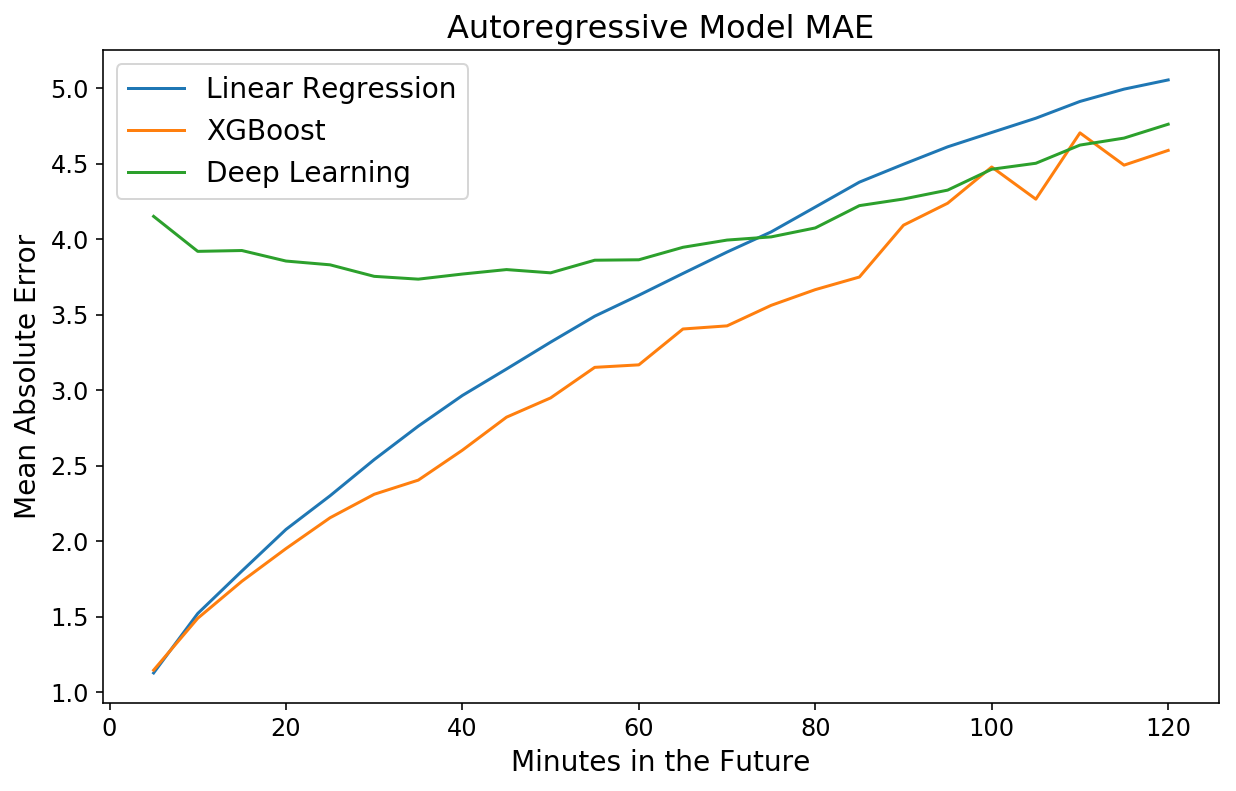
Seltsamerweise ist das Modell für nahe in der Zukunft liegende Zeitpunkte schlechter, aber für 2-Stunden-Vorhersagen ungefähr gleichauf mit XGBoost. Dies ist ein weiteres Beispiel für die Leistungsfähigkeit und Benutzerfreundlichkeit von XGBoost.
Ich bin immer wieder erstaunt, wie 1) schnell und 2) strong gegenüber Überanpassung XGBoost ist. Mit Abstand meine Lieblingsbibliothek für maschinelles Lernen.
— Sean J. Taylor (@seanjtaylor) 1. März 2017
Erkenntnisse
In diesem Beitrag habe ich gezeigt, wie man die Sketche Bibliothek zum Trainieren eines überwachten Lernmodells zur direkten Vorhersage einer Zeitreihe Horizont. Wir haben dann die Komplexität unserer Modelle ganz einfach gesteigert, indem wir komplexere Modelle in unsere Scikit-Be taught-Pipeline eingefügt haben. Im besten Fall konnten wir die Anzahl der Fahrräder an der Fahrradverleihstation bei meiner Wohnung 2 Stunden im Voraus auf 4,5 Fahrräder genau vorhersagen.
Ich sollte anmerken, dass dieser Beitrag keine vollständig wissenschaftliche Studie warfare. Dazu hätte ich Trainings-, Validierungs- und Testdatensätze erstellen müssen. Außerdem hätte ich eine richtige Hyperparametersuche durchführen müssen (insbesondere für das Deep-Studying-Modell!). Trotzdem bin ich weiterhin zuversichtlich, dass wir bei der Horizontvorhersage gute Arbeit leisten können.
Wie können wir das besser machen? Es gibt eine Reihe von Möglichkeiten, die ich in weiteren Blogbeiträgen näher untersuchen möchte. Anstatt unsere Daten zur Fahrradverfügbarkeit als kontinuierliche Zeitreihe zu betrachten, die es vorherzusagen gilt, könnten wir einen ähnlichen Ansatz wählen wie ordinale Regression. Zusätzlich können wir Informationen von anderen Fahrradstationen einbeziehen, um unsere jeweilige Station besser vorherzusagen. Bleiben Sie dran!
