Kurz zusammengefasst: Beim RLHF besteht eine Spannung zwischen der Belohnungslernphase, die menschliche Vorlieben in Type von Vergleichen nutzt, und der RL-Feinabstimmungsphase, die eine einzelne, nicht vergleichende Belohnung optimiert. Was wäre, wenn wir RL vergleichend durchführen würden?
Abbildung 1:
Dieses Diagramm veranschaulicht den Unterschied zwischen dem bestärkenden Lernen und absolut Suggestions und relativ Suggestions. Durch die Einbindung einer neuen Komponente – des paarweisen Coverage-Gradienten – können wir die Belohnungsmodellierungsphase und die RL-Part vereinheitlichen und direkte Updates basierend auf paarweisen Antworten ermöglichen.
Giant Language Fashions (LLMs) ermöglichen immer leistungsfähigere virtuelle Assistenten, wie zum Beispiel GPT-4, Claude-2, Barde Und Bing-Chat. Diese Systeme können auf komplexe Benutzeranfragen reagieren, Code schreiben und sogar Gedichte produzieren. Die Technik, die diesen erstaunlichen virtuellen Assistenten zugrunde liegt, ist Reinforcement Studying mit menschlichem Suggestions (RLHF). RLHF zielt darauf ab, das Modell an menschlichen Werten auszurichten und unbeabsichtigtes Verhalten zu eliminieren, das häufig dadurch entstehen kann, dass das Modell während der Vortrainingsphase einer großen Menge minderwertiger Daten ausgesetzt ist.
Proximale Richtlinienoptimierung (PPO), der dominierende RL-Optimierer in diesem Prozess, weist Berichten zufolge Instabilität Und Komplikationen bei der Implementierung. Noch wichtiger ist, dass es im RLHF-Prozess eine anhaltende Diskrepanz gibt: Obwohl das Belohnungsmodell durch Vergleiche zwischen verschiedenen Antworten trainiert wird, arbeitet die RL-Feinabstimmungsphase an einzelnen Antworten, ohne Vergleiche anzustellen. Diese Inkonsistenz kann Probleme verschärfen, insbesondere im anspruchsvollen Bereich der Sprachgenerierung.
Vor diesem Hintergrund stellt sich eine spannende Frage: Ist es möglich, einen RL-Algorithmus zu entwickeln, der vergleichend lernt? Um dies zu untersuchen, führen wir die Pairwise Proximal Coverage Optimization (P3O), eine Methode, die die Trainingsprozesse sowohl in der Belohnungslernphase als auch in der RL-Feinabstimmungsphase von RLHF harmonisiert und eine zufriedenstellende Lösung für dieses Drawback bietet.
Hintergrund
Figur 2:
Eine Beschreibung der drei Stadien des RLHF aus der Sicht eines OpenAI-Blogbeitrag. Beachten Sie, dass die dritte Part unter das bestärkende Lernen mit absolutem Suggestions fällt, wie auf der linken Seite von Abbildung 1 dargestellt.
In herkömmlichen RL-Einstellungen wird die Belohnung manuell vom Entwickler festgelegt oder durch eine intestine definierte Belohnungsfunktion bereitgestellt, wie in Atari-Spielen. Um ein Modell jedoch in Richtung hilfreicher und harmloser Reaktionen zu lenken, ist es nicht einfach, eine gute Belohnung zu definieren. RLHF behebt dieses Drawback, indem die Belohnungsfunktion aus menschlichem Suggestions, insbesondere in Type von Vergleichen, gelernt wird und dann RL angewendet wird, um die gelernte Belohnungsfunktion zu optimieren.
Die RLHF-Pipeline ist in mehrere Phasen unterteilt, die im Folgenden detailliert beschrieben werden:
Überwachte Feinabstimmungsphase: Das vortrainierte Modell erfährt den maximalen Wahrscheinlichkeitsverlust auf einem hochwertigen Datensatz, wo es durch Nachahmung lernt, auf menschliche Anfragen zu reagieren.
Part der Belohnungsmodellierung: Das SFT-Modell wird mit Eingabeaufforderungen (x) aufgefordert, Antwortpaare (y_1,y_2sim pi^{textual content{SFT}}(yvert x)) zu erzeugen. Diese generierten Antworten bilden einen Datensatz. Die Antwortpaare werden menschlichen Etikettierern präsentiert, die eine Präferenz für eine Antwort gegenüber der anderen ausdrücken, bezeichnet als (y_w succ y_l). Ein komparativer Verlust wird dann verwendet, um ein Belohnungsmodell (r_phi) zu trainieren:
(mathcal{L}_R = mathbb{E}_{(x,y_l,y_w)simmathcal{D}}log sigmaleft(r_phi(y_w|x)-r_phi(y_l|x)proper))
RL Feinabstimmungsphase: Das SFT-Modell dient als Initialisierung dieser Part, und ein RL-Algorithmus optimiert die Strategie zur Maximierung der Belohnung und begrenzt gleichzeitig die Abweichung von der ursprünglichen Strategie. Formal geschieht dies durch:
(max_{pi_theta}mathbb{E}_{xsim mathcal{D}, ysim pi_theta(cdotvert x)}left(r_phi(yvert x)-beta D_{textual content{KL}}(pi_theta(cdotvert x)Vert pi^{textual content{SFT}}(cdotvert x))proper))
Eine inhärente Herausforderung bei diesem Ansatz ist die Nichteindeutigkeit der Belohnung. Wenn beispielsweise eine Belohnungsfunktion (r(yvert x)) gegeben ist, erzeugt eine einfache Verschiebung der Belohnung der Eingabeaufforderung auf (r(yvert x)+delta(x)) eine weitere gültige Belohnungsfunktion. Diese beiden Belohnungsfunktionen führen bei allen Antwortpaaren zum gleichen Verlust, unterscheiden sich jedoch erheblich, wenn sie mit RL optimiert werden. Im Extremfall, wenn das hinzugefügte Rauschen dazu führt, dass die Belohnungsfunktion einen großen Bereich aufweist, könnte ein RL-Algorithmus dazu verleitet werden, die Wahrscheinlichkeit von Antworten mit höheren Belohnungen zu erhöhen, obwohl diese Belohnungen möglicherweise nicht sinnvoll sind. Mit anderen Worten, die Richtlinie könnte durch die Informationen zur Belohnungsskala in der Eingabeaufforderung (x) gestört werden, lernt jedoch nicht den nützlichen Teil – die relative Präferenz, die durch den Belohnungsunterschied dargestellt wird. Um dieses Drawback zu lösen, ist es unser Ziel, einen RL-Algorithmus zu entwickeln, der invariante zur Belohnungsübersetzung.
Ableitung von P3O
Unsere Idee stammt aus dem Vanilla-Coverage-Gradienten (VPG). VPG ist ein weit verbreiteter RL-Optimierer erster Ordnung, der wegen seiner Einfachheit und einfachen Implementierung beliebt ist. In einem kontextuellen Banditen (CB) Einstellung wird das VPG wie folgt formuliert:
(nabla mathcal{L}^{textual content{VPG}} = mathbb{E}_{ysimpi_{theta}} r(y|x)nablalogpi_{theta }(y|x))
Durch einige algebraische Manipulationen können wir den Coverage-Gradienten in eine vergleichende Type umschreiben, die zwei Antworten auf dieselbe Eingabe beinhaltet. Wir nennen ihn Paarweiser Richtliniengradient:
(mathbb{E}_{y_1,y_2simpi_{theta}}left(r(y_1vert x)-r(y_2vert x)proper)nablaleft(logfrac{pi_theta(y_1vert x)}{pi_theta(y_2vert x)}proper)/2)
Im Gegensatz zu VPG, das direkt auf der absoluten Höhe der Belohnung beruht, verwendet PPG die Belohnungsdifferenz. Dadurch können wir das oben erwähnte Drawback der Belohnungsübersetzung umgehen. Um die Leistung weiter zu steigern, integrieren wir einen Wiedergabepuffer mit Wichtigkeitsstichproben und vermeiden Sie große Gradientenaktualisierungen über Ausschnitt.
Wichtigkeitsstichproben: Wir entnehmen eine Reihe von Antworten aus dem Wiedergabepuffer, die aus Antworten bestehen, die von (pi_{textual content{previous}}) generiert wurden, und berechnen dann das Wichtigkeits-Stichprobenverhältnis für jedes Antwortpaar. Der Gradient ist die gewichtete Summe der Gradienten, die aus jedem Antwortpaar berechnet wurden.
Ausschnitt: Wir kürzen das Significance-Sampling-Verhältnis sowie das Gradienten-Replace, um übermäßig große Updates zu bestrafen. Diese Technik ermöglicht dem Algorithmus, KL-Divergenz und Belohnung effizienter auszugleichen.
Es gibt zwei verschiedene Möglichkeiten, die Clipping-Technik zu implementieren, die sich durch separates oder gemeinsames Clipping unterscheiden. Der resultierende Algorithmus wird als Pairwise Proximal Coverage Optimization (P3O) bezeichnet, wobei die Varianten V1 bzw. V2 sind. Weitere Einzelheiten finden Sie in unserem Authentic Papier.
Auswertung
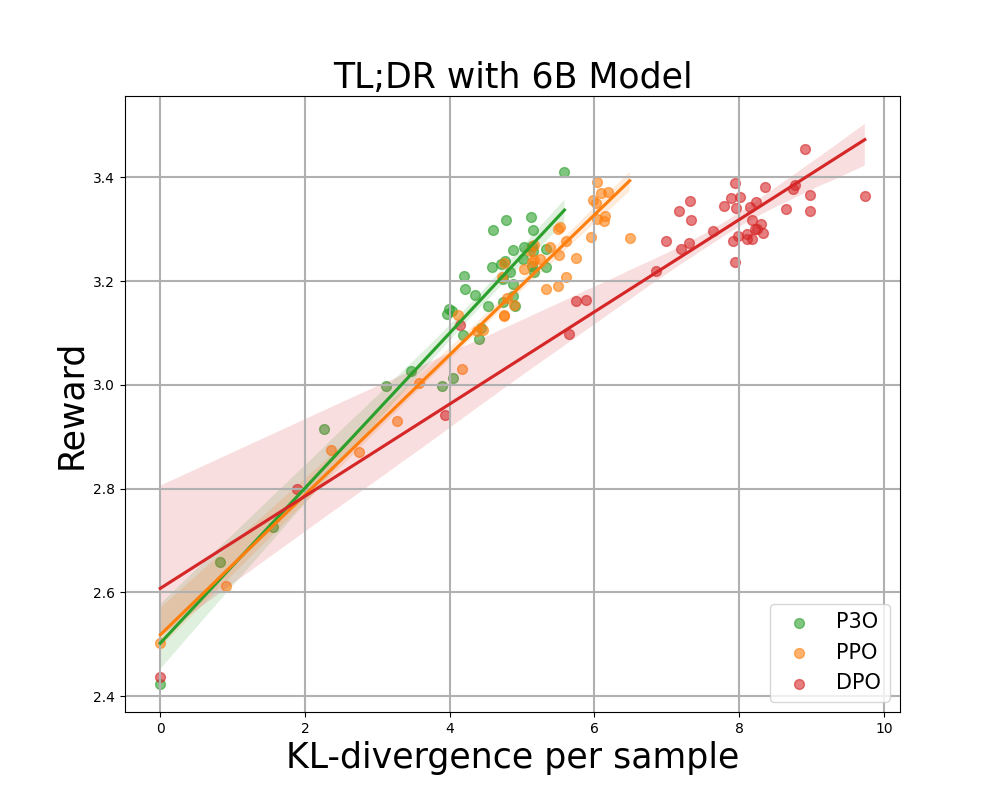
Figur 3:
KL-Belohnungsgrenze für TL;DR, sowohl sequenzweise KL als auch Belohnung werden über 200 Testaufforderungen gemittelt und alle 500 Gradientenschritte berechnet. Wir stellen fest, dass eine einfache lineare Funktion intestine zur Kurve passt. P3O hat von den dreien den besten KL-Belohnungs-Kompromiss.
Wir untersuchen zwei verschiedene offene Textgenerierungsaufgaben, Zusammenfassung Und Fragen und AntwortenZusammenfassend verwenden wir die Kurz zusammengefasst Datensatz, bei dem die Eingabeaufforderung (x) ein Forumsbeitrag von Reddit und (y) eine entsprechende Zusammenfassung ist. Zur Beantwortung von Fragen verwenden wir Anthropic Useful and Innocent (HH), ist die Eingabeaufforderung (x) eine menschliche Abfrage aus verschiedenen Themenbereichen, und die Richtlinie sollte lernen, eine ansprechende und hilfreiche Antwort (y) zu produzieren.
Wir vergleichen unseren Algorithmus P3O mit mehreren effektiven und repräsentativen Ansätzen für die LLM-Ausrichtung. Wir beginnen mit dem SFT Strategie, die mit maximaler Wahrscheinlichkeit trainiert wird. Für RL-Algorithmen betrachten wir den dominanten Ansatz PPO und die neu vorgeschlagene Datenschutzbeauftragter. DPO optimiert die Richtlinie direkt in Richtung der geschlossenen Lösung des KL-beschränkten RL-Issues. Obwohl es als Offline-Ausrichtungsmethode vorgeschlagen wird, machen wir es mithilfe einer Proxy-Belohnungsfunktion on-line.
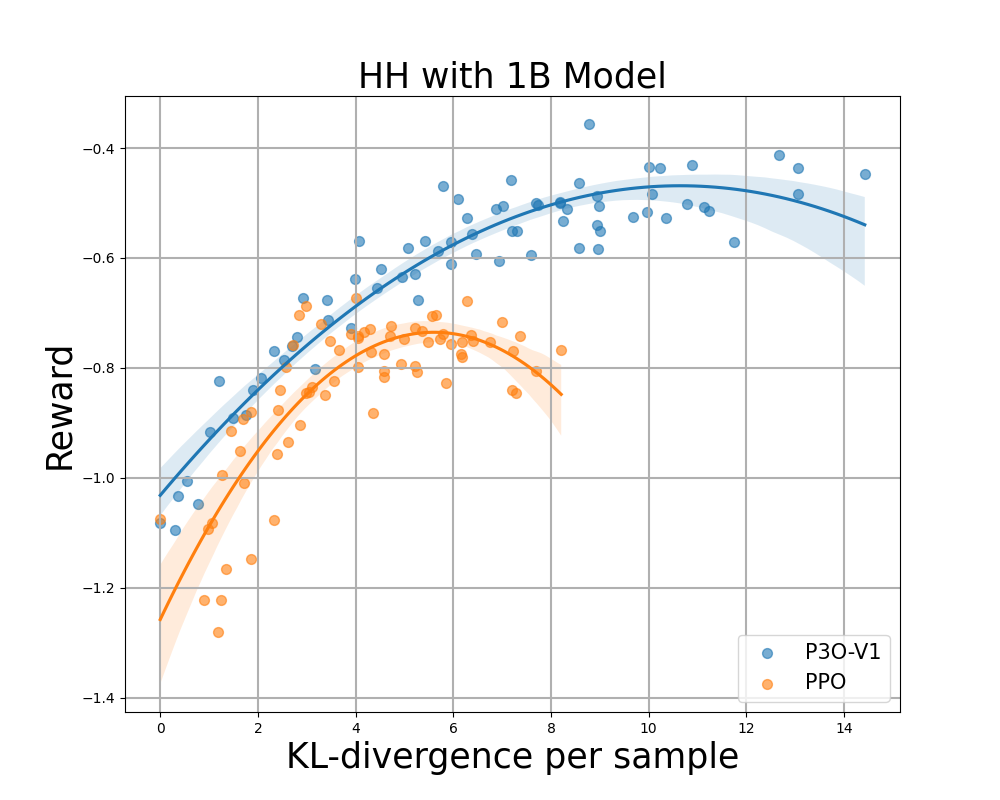
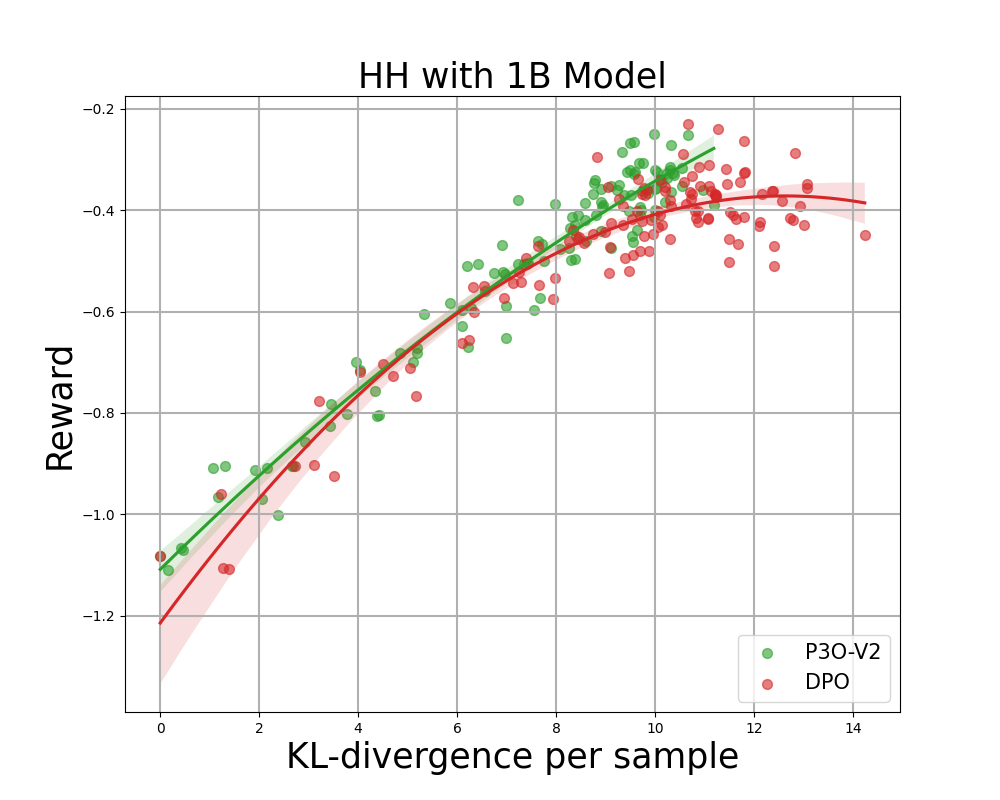
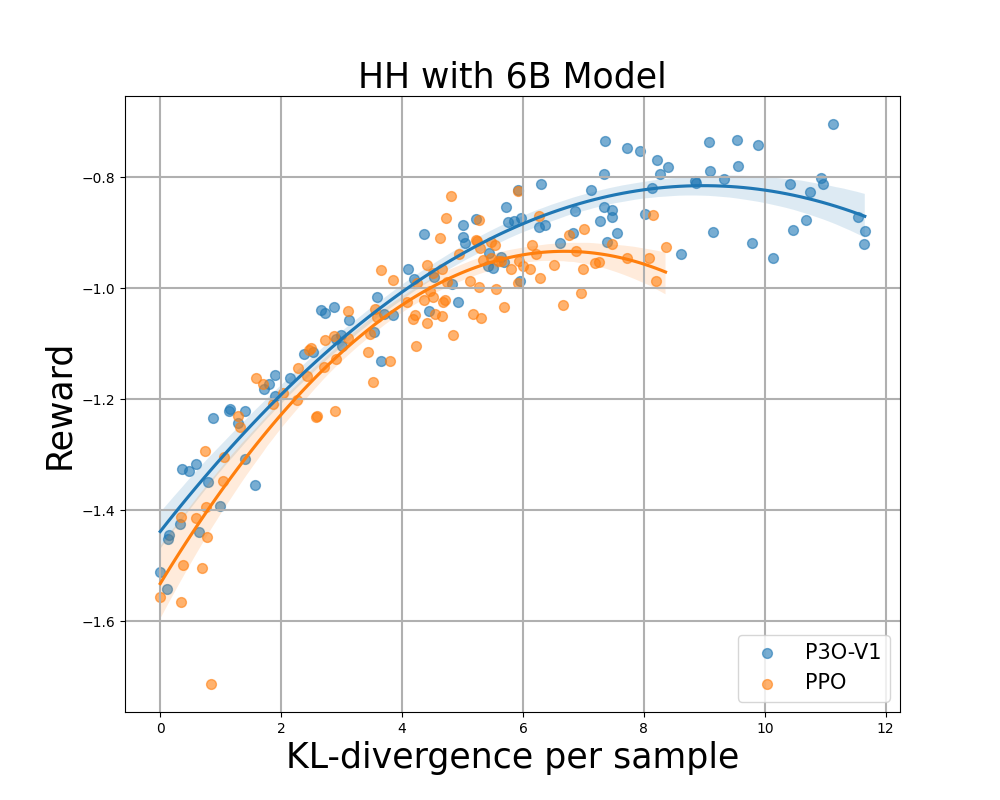
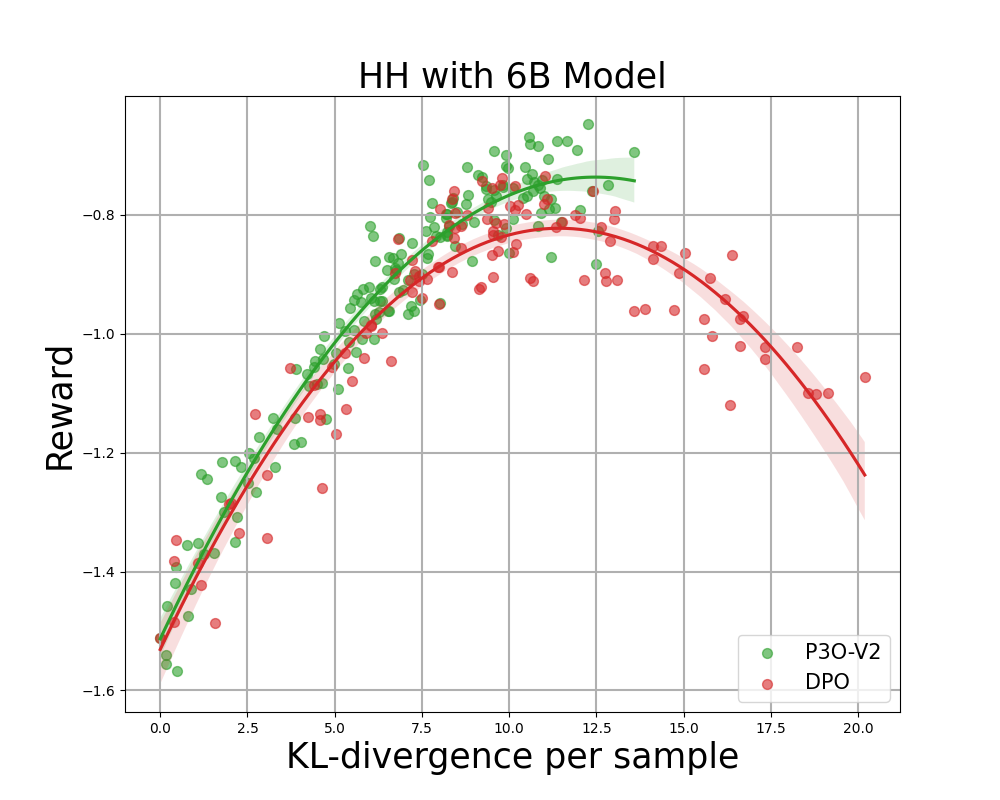
Figur 4:
KL-Belohnungsgrenze für HH, jeder Punkt stellt einen Durchschnitt der Ergebnisse von 280 Testaufforderungen dar und wird alle 500 Gradientenaktualisierungen berechnet. Die beiden linken Abbildungen vergleichen P3O-V1 und PPO mit unterschiedlichen Basismodellgrößen; die beiden rechten Abbildungen vergleichen P3O-V2 und DPO. Die Ergebnisse zeigen, dass P3O nicht nur eine höhere Belohnung erzielen kann, sondern auch eine bessere KL-Kontrolle bietet.
Eine zu große Abweichung von der Referenzrichtlinie würde dazu führen, dass die On-line-Richtlinie das Belohnungsmodell abschneidet und inkohärente Fortsetzungen produziert, wie in früheren Arbeiten gezeigt wurde. Uns interessiert nicht nur die in der RL-Literatur intestine etablierte Metrik – die Belohnung –, sondern auch, wie weit die erlernte Richtlinie von der ursprünglichen Richtlinie abweicht, gemessen an der KL-Divergenz. Daher untersuchen wir die Wirksamkeit jedes Algorithmus anhand seiner Grenze der erreichten Belohnung und der KL-Divergenz von der Referenzrichtlinie (KL-Belohnungsgrenze). In Abbildung 4 und Abbildung 5 stellen wir fest, dass P3O bei verschiedenen Modellgrößen streng dominante Grenzen als PPO und DPO aufweist.
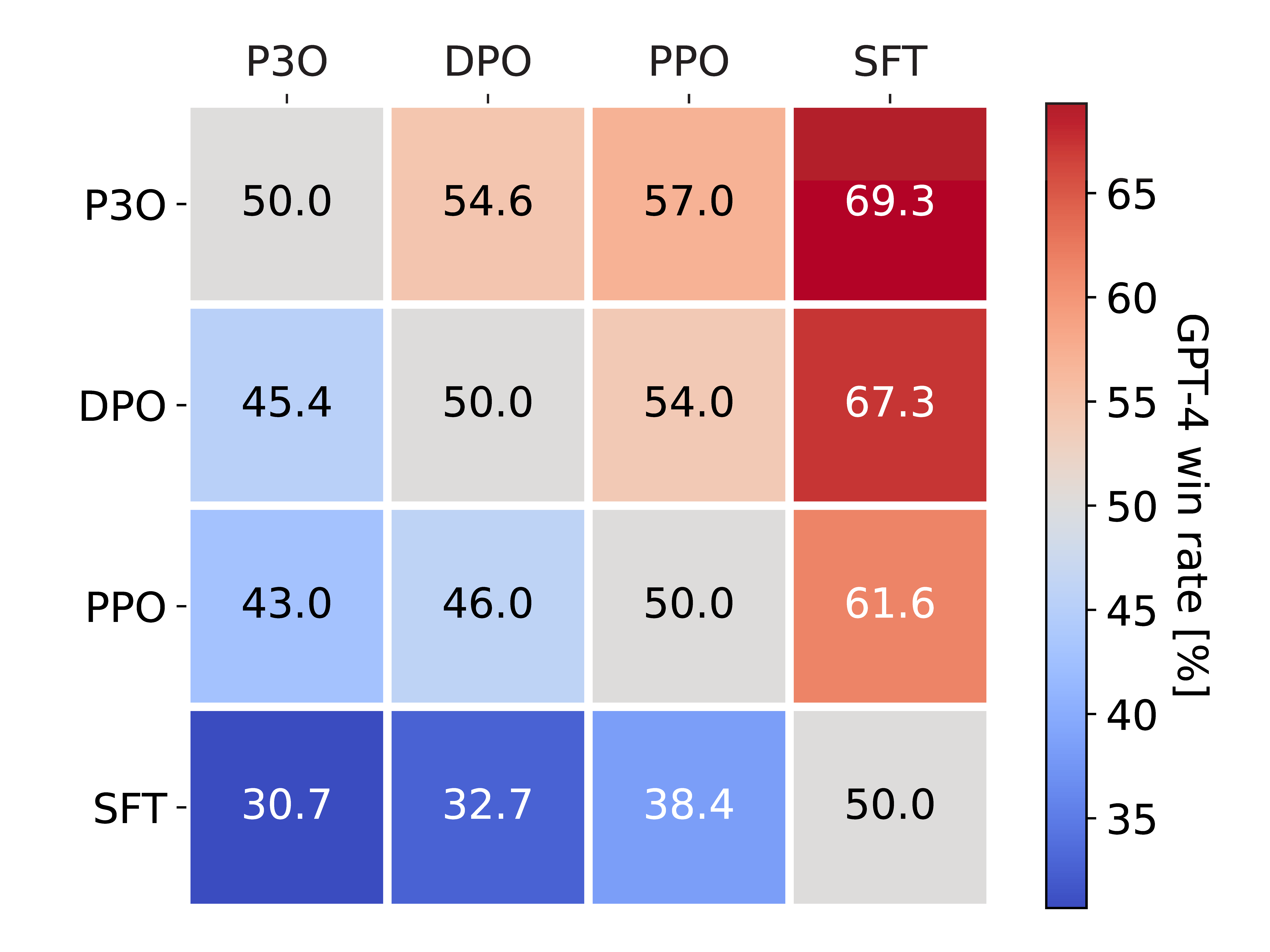
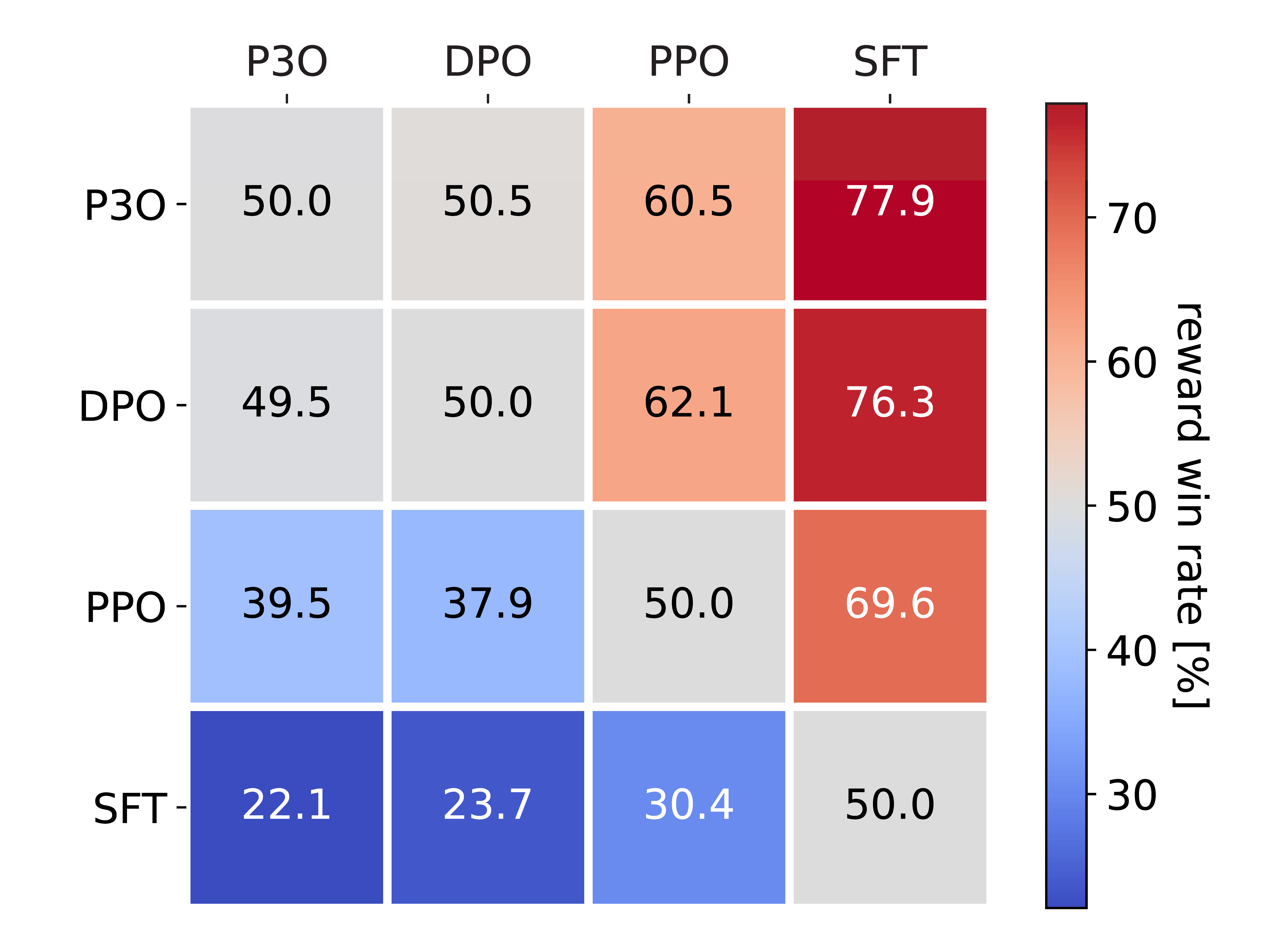
Abbildung 5:
Die linke Abbildung zeigt die von GPT-4 ausgewertete Gewinnrate. Die rechte Abbildung zeigt die Gewinnrate basierend auf dem direkten Vergleich der Proxy-Belohnung. Trotz der hohen Korrelation zwischen den beiden Zahlen haben wir festgestellt, dass die Belohnungsgewinnrate entsprechend dem KL angepasst werden muss, um mit der GPT-4-Gewinnrate übereinzustimmen.
Um die Qualität der generierten Antworten direkt zu beurteilen, führen wir auch Head-to-Head-Vergleiche zwischen jedem Algorithmenpaar im HH-Datensatz. Wir verwenden zwei Metriken zur Bewertung: (1) Belohnendas optimierte Ziel während des On-line-RL, (2) GPT-4als zuverlässiger Indikator für die menschliche Bewertung der Nützlichkeit von Antworten. Für letztere Metrik weisen wir darauf hin, dass frühere Studien gezeigt haben, dass GPT-4-Urteile stark mit Menschen korrelieren, wobei die menschliche Übereinstimmung mit GPT-4 typischerweise ähnlich oder höher ist als die Übereinstimmung zwischen menschlichen Annotatoren.
Abbildung 5 zeigt die umfassenden Ergebnisse des paarweisen Vergleichs. Die durchschnittliche KL-Divergenz und Belohnungsrangfolge dieser Modelle lautet DPO > P3O > PPO > SFT. Obwohl DPO P3O in der Belohnung geringfügig übertrifft, weist es eine erheblich höhere KL-Divergenz auf, was sich nachteilig auf die Qualität der Generierung auswirken kann. Infolgedessen hat DPO eine Belohnungsgewinnrate von 49,5 % gegenüber P3O, aber nur 45,4 %, wie von GPT-4 bewertet. Im Vergleich zu anderen Methoden weist P3O eine GPT-4-Gewinnrate von 57,0 % gegenüber PPO und 69,3 % gegenüber SFT auf. Dieses Ergebnis steht im Einklang mit unseren Erkenntnissen aus der KL-Belohnungsgrenzmetrik und bestätigt, dass P3O sich besser an die menschlichen Vorlieben anpassen könnte als frühere Basislinien.
Abschluss
In diesem Blogbeitrag präsentieren wir neue Erkenntnisse zur Anpassung großer Sprachmodelle an menschliche Vorlieben durch bestärkendes Lernen. Wir haben das Framework „Bestärkendes Lernen mit relativem Suggestions“ vorgeschlagen, wie in Abbildung 1 dargestellt. In diesem Framework entwickeln wir einen neuartigen Coverage-Gradient-Algorithmus – P3O. Dieser Ansatz vereint die grundlegenden Prinzipien der Belohnungsmodellierung und der Feinabstimmung von RL durch vergleichendes Coaching. Unsere Ergebnisse zeigen, dass P3O frühere Methoden in Bezug auf die KL-Belohnungsgrenze sowie die GPT-4-Gewinnrate übertrifft.
BibTex
Dieser Weblog basiert auf unserer jüngsten Papier Und Weblog. Wenn dieser Weblog Sie zu Ihrer Arbeit inspiriert, denken Sie bitte daran, ihn wie folgt zu zitieren:
@article{wu2023pairwise,
title={Pairwise Proximal Coverage Optimization: Harnessing Relative Suggestions for LLM Alignment},
creator={Wu, Tianhao and Zhu, Banghua and Zhang, Ruoyu and Wen, Zhaojin and Ramchandran, Kannan and Jiao, Jiantao},
journal={arXiv preprint arXiv:2310.00212},
yr={2023}
}
