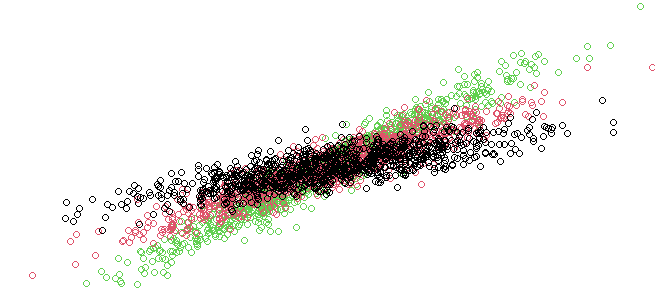
Die lineare Regression wird normalerweise als nicht flexibel genug angesehen, um die nichtlinearen Daten zu bewältigen. Aus theoretischer Sicht ist es nicht möglich, mit ihnen umzugehen. Wir können es jedoch mit jedem Datensatz zum Laufen bringen, indem wir endliche Normalmischungen in einem Regressionsmodell verwenden. Auf diese Weise wird es zu einem sehr leistungsstarken Werkzeug für maschinelles Lernen, das auf praktisch jeden Datensatz angewendet werden kann, selbst auf stark unnormale Datensätze mit nichtlinearen Abhängigkeiten zwischen den Variablen.
Was diesen Ansatz besonders interessant macht, ist seine Interpretierbarkeit. Trotz einer äußerst hohen Flexibilität können alle erkannten Zusammenhänge direkt interpretiert werden. Das Modell ist so allgemein wie ein neuronales Netzwerk, wird jedoch nicht zu einer Blackbox. Sie können die Beziehungen lesen und die Auswirkungen einzelner Variablen verstehen.
In diesem Beitrag zeigen wir, wie man ein Finite-Mischungs-Modell für die Regression mithilfe der Markov-Chain-Monte-Carlo-Stichprobe (MCMC) simuliert. Wir werden Daten mit mehreren Komponenten (Gruppen) generieren und ein Mischungsmodell anpassen, um diese Komponenten mithilfe der Bayes’schen Inferenz wiederherzustellen. Dieser Prozess umfasst Regressionsmodelle und Mischungsmodelle und kombiniert sie mit MCMC-Techniken zur Parameterschätzung.
Wir beginnen mit dem Laden der notwendigen Bibliotheken, um mit Regressionsmodellen, MCMC und multivariaten Verteilungen zu arbeiten
# Loading the required libraries for varied features
library("pscl") # For pscl particular features, like regression fashions
library("MCMCpack") # For MCMC sampling features, together with posterior distributions
library(mvtnorm) # For multivariate regular distribution functio
- pscl: Wird für verschiedene statistische Funktionen wie Regressionsmodelle verwendet.
- MCMCpack: Enthält Funktionen für Bayes’sche Inferenz, insbesondere MCMC-Stichprobe.
- mvtnorm: Bietet Werkzeuge zum Arbeiten mit multivariaten Normalverteilungen.
Wir simulieren einen Datensatz, in dem jede Beobachtung zu einer von mehreren Gruppen (Komponenten des Mischungsmodells) gehört und die Antwortvariable mithilfe eines Regressionsmodells mit Zufallskoeffizienten generiert wird.
Wir betrachten einen allgemeinen Aufbau für ein Regressionsmodell unter Verwendung von G-Normalmischungskomponenten.
## Generate the observations
# Set the size of the time collection (variety of observations per group)
N <- 1000
# Set the variety of simulations (iterations of the MCMC course of)
nSim <- 200
# Set the variety of parts within the combination mannequin (G is the variety of teams)
G <- 3
- N: Die Anzahl der Beobachtungen professional Gruppe.
- nSim: Die Anzahl der MCMC-Iterationen.
- G: Die Anzahl der Komponenten (Gruppen) in unserem Mischungsmodell.
Daten simulieren
Jede Gruppe wird mithilfe eines univariaten Regressionsmodells modelliert, bei dem die erklärenden Variablen (X) und die Antwortvariable (y) aus Normalverteilungen simuliert werden. Der betas stellen die Regressionskoeffizienten für jede Gruppe dar und sigmas stellen die Varianz für jede Gruppe dar.
# Set the values for the regression coefficients (betas) for every group
betas <- 1:sum(dimG) * 2.5 # Producing sequential betas with a multiplier of two.5
# Outline the variance (sigma) for every element (group) within the combination
sigmas <- rep(1, G) / 1 # Set variance to 1 for every element, with a hard and fast divisor of 1
- Betas: Dies sind die Regressionskoeffizienten. Der Koeffizient jeder Gruppe wird nacheinander zugewiesen.
- Sigmas: Stellt die Varianz für jede Gruppe im Mischungsmodell dar.
In diesem Modell ermöglichen wir, dass jede Mischungskomponente ihren eigenen Varianzparameter und einen Satz von Regressionsparametern besitzt.
Gruppenzuweisung und Mischung
Anschließend simulieren wir die Gruppenzuordnung jeder Beobachtung anhand einer Zufallszuordnung und mischen die Daten für alle Komponenten.
Wir erweitern das Modell um eine Reihe von Komponentenbeschriftungsvektoren für
Wo
und somit z_gi=1 impliziert, dass die ich-Das Individuum wird aus dem gezogen G-te Komponente der Mischung.
Diese zufällige Zuordnung bildet die z_original Vektor, der die wahre Gruppe darstellt, zu der jede Beobachtung gehört.
# Initialize the unique group assignments (z_original)
z_original <- matrix(NA, N * G, 1)
# Repeat every group label N instances (assign labels to every statement per group)
z_original <- rep(1:G, rep(N, G))
# Resample the information rows by random order
sampled_order <- pattern(nrow(knowledge))
# Apply the resampled order to the information
knowledge <- knowledge(sampled_order,)
Wir legen Vorverteilungen für die Regressionskoeffizienten und Varianzen fest. Diese Prioritäten werden unsere Bayes’sche Schätzung leiten.
## Outline Priors for Bayesian estimation# Outline the prior imply (muBeta) for the regression coefficients
muBeta <- matrix(0, G, 1)# Outline the prior variance (VBeta) for the regression coefficients
VBeta <- 100 * diag(G) # Massive variance (100) as a previous for the beta coefficients# Prior for the sigma parameters (variance of every element)
ag <- 3 # Form parameter
bg <- 1/2 # Price parameter for the prior on sigma
shSigma <- ag
raSigma <- bg^(-1)
- muBeta: Der vorherige Mittelwert für die Regressionskoeffizienten. Wir setzen es für alle Komponenten auf 0.
- VBeta: Die vorherige Varianz, die groß ist (100), um Flexibilität bei den Koeffizienten zu ermöglichen.
- shSigma Und raSigma: Type- und Ratenparameter für den Prior der Varianz (Sigma) jeder Gruppe.
Für die Komponentenindikatoren und Komponentenwahrscheinlichkeiten berücksichtigen wir folgende vorherige Zuordnung
Der multinomiale Prior M ist die multivariate Verallgemeinerung des Binomials, und der Dirichlet-Prior D ist eine multivariate Verallgemeinerung der Betaverteilung.
In diesem Abschnitt initialisieren wir den MCMC-Prozess, indem wir Matrizen einrichten, um die Stichproben der Regressionskoeffizienten, Varianzen und Mischungsverhältnisse zu speichern.
## Initialize MCMC sampling# Initialize matrix to retailer the samples for beta
mBeta <- matrix(NA, nSim, G)# Assign the primary worth of beta utilizing a random regular distribution
for (g in 1:G) {
mBeta(1, g) <- rnorm(1, muBeta(g, 1), VBeta(g, g))
}# Initialize the sigma^2 values (variance for every element)
mSigma2 <- matrix(NA, nSim, G)
mSigma2(1, ) <- rigamma(1, shSigma, raSigma)# Initialize the blending proportions (pi), utilizing a Dirichlet distribution
mPi <- matrix(NA, nSim, G)
alphaPrior <- rep(N/G, G) # Prior for the blending proportions, uniform throughout teams
mPi(1, ) <- rdirichlet(1, alphaPrior)
- mBeta: Matrix zum Speichern von Stichproben der Regressionskoeffizienten.
- mSigma2: Matrix zum Speichern der Varianzen (Sigma-Quadrat) für jede Komponente.
- mPi: Matrix zur Speicherung der Mischungsverhältnisse, initialisiert mit einer Dirichlet-Verteilung.
Wenn wir von den Werten der Komponentenindikatorvariablen z abhängig machen, kann die bedingte Wahrscheinlichkeit ausgedrückt werden als:
In der MCMC-Sampling-Schleife aktualisieren wir die Gruppenzuweisungen (z), Regressionskoeffizienten (beta) und Varianzen (sigma) basierend auf den Posteriorverteilungen. Die Wahrscheinlichkeit jeder Gruppenzuordnung wird berechnet und die Gruppe mit der höchsten A-Posteriori-Wahrscheinlichkeit wird ausgewählt.
Die folgenden vollständigen hinteren Konditionale können erhalten werden:
Wo
bezeichnet alle Parameter in unserem Posterior außer X.
und wo n_g bezeichnet die Anzahl der Beobachtungen im G-te Komponente der Mischung.
Und
Der folgende Algorithmus greift in sequentieller Reihenfolge auf die Reihe der Posterior-Verteilungen oben zurück.
## Begin the MCMC iterations for posterior sampling# Loop over the variety of simulations
for (i in 2:nSim) {
print(i) # Print the present iteration quantity# For every statement, replace the group project (z)
for (t in 1:(N*G)) {
fig <- NULL
for (g in 1:G) {
# Calculate the probability of every group and the corresponding posterior likelihood
fig(g) <- dnorm(y(t, 1), X(t, ) %*% mBeta(i-1, g), sqrt(mSigma2(i-1, g))) * mPi(i-1, g)
}
# Keep away from zero probability and regulate it
if (all(fig) == 0) {
fig <- fig + 1/G
}
# Pattern a brand new group project based mostly on the posterior chances
z(i, t) <- which(rmultinom(1, 1, fig/sum(fig)) == 1)
}
# Replace the regression coefficients for every group
for (g in 1:G) {
# Compute the posterior imply and variance for beta (utilizing the information for group g)
DBeta <- clear up(t(X(z(i, ) == g, )) %*% X(z(i, ) == g, ) / mSigma2(i-1, g) + clear up(VBeta(g, g)))
dBeta <- t(X(z(i, ) == g, )) %*% y(z(i, ) == g, 1) / mSigma2(i-1, g) + clear up(VBeta(g, g)) %*% muBeta(g, 1)
# Pattern a brand new worth for beta from the multivariate regular distribution
mBeta(i, g) <- rmvnorm(1, DBeta %*% dBeta, DBeta)
# Replace the variety of observations in group g
ng(i, g) <- sum(z(i, ) == g)
# Replace the variance (sigma^2) for every group
mSigma2(i, g) <- rigamma(1, ng(i, g)/2 + shSigma, raSigma + 1/2 * sum((y(z(i, ) == g, 1) - (X(z(i, ) == g, ) * mBeta(i, g)))^2))
}
# Reorder the group labels to keep up consistency
reorderWay <- order(mBeta(i, ))
mBeta(i, ) <- mBeta(i, reorderWay)
ng(i, ) <- ng(i, reorderWay)
mSigma2(i, ) <- mSigma2(i, reorderWay)
# Replace the blending proportions (pi) based mostly on the variety of observations in every group
mPi(i, ) <- rdirichlet(1, alphaPrior + ng(i, ))
}
Dieser Codeblock führt die wichtigsten Schritte in MCMC aus:
- Aktualisierung der Gruppenzuweisung: Für jede Beobachtung berechnen wir die Wahrscheinlichkeit, dass die Daten zu jeder Gruppe gehören, und aktualisieren die Gruppenzuordnung entsprechend.
- Aktualisierung des Regressionskoeffizienten: Die Regressionskoeffizienten für jede Gruppe werden anhand des hinteren Mittelwerts und der Varianz aktualisiert, die auf der Grundlage der beobachteten Daten berechnet werden.
- Varianzaktualisierung: Die Varianz der Antwortvariablen für jede Gruppe wird mithilfe der inversen Gammaverteilung aktualisiert.
Abschließend visualisieren wir die Ergebnisse der MCMC-Probenahme. Wir zeichnen die Posteriorverteilungen für jeden Regressionskoeffizienten auf, vergleichen sie mit den wahren Werten und zeichnen die wahrscheinlichsten Gruppenzuordnungen auf.
# Plot the posterior distributions for every beta coefficient
par(mfrow=c(G,1))
for (g in 1:G) {
plot(density(mBeta(5:nSim, g)), major = 'True parameter (vertical) and the distribution of the samples') # Plot the density for the beta estimates
abline(v = betas(g)) # Add a vertical line on the true worth of beta for comparability
}
Dieses Diagramm zeigt, wie die MCMC-Stichproben (posteriore Verteilung) für die Regressionskoeffizienten zu den wahren Werten konvergieren (betas).
Durch diesen Prozess haben wir gezeigt, wie endliche Normalmischungen in einem Regressionskontext in Kombination mit MCMC zur Parameterschätzung verwendet werden können. Indem wir Daten mit bekannten Gruppierungen simulieren und die Parameter durch Bayes’sche Inferenz wiederherstellen, können wir beurteilen, wie intestine unser Modell die zugrunde liegende Struktur der Daten erfasst.
Sofern nicht anders angegeben, stammen alle Bilder vom Autor.