Blase Diagramme Den elegant große Mengen an Informationen in eine einzelne Visualisierung zusammendrücken, wobei die Blasengröße eine dritte Dimension hinzufügt. Der Vergleich von „vor“ und „Nachher“ -Staaten ist jedoch oft von entscheidender Bedeutung. Um dies anzugehen, schlagen wir vor, einen Übergang zwischen diesen Zuständen hinzuzufügen und eine intuitive Benutzererfahrung zu schaffen.
Da wir keine fertige Lösung finden konnten, haben wir unsere eigenen entwickelt. Die Herausforderung stellte sich als faszinierend heraus und erforderte einige mathematische Konzepte.
Ohne Zweifel ist der schwierigste Teil der Visualisierung der Übergang zwischen zwei Kreisen – vor und nach den Zuständen. Um zu vereinfachen, konzentrieren wir uns auf die Lösung eines einzelnen Falls, der dann in einer Schleife erweitert werden kann, um die erforderliche Anzahl von Übergängen zu erzeugen.

Um eine solche Figur aufzubauen, zersetzen wir sie zuerst in drei Teile: zwei Kreise und ein Polygon, das sie verbindet (in Grau).

Es ist recht einfach, zwei Kreise zu bauen – wir kennen ihre Zentren und Radien. Die verbleibende Aufgabe besteht darin, ein viereckiges Polygon zu konstruieren, das die folgende Type hat:

Die Konstruktion dieses Polygons reduziert sich auf die Suche nach den Koordinaten seiner Eckpunkte. Dies ist die interessanteste Aufgabe, und wir werden sie weiter lösen.

Um den Abstand von einem Punkt zu berechnen (x1, y1) zur Linie Ax+y+b = 0Die Formel lautet:

In unserem Fall Entfernung (D) ist gleich dem Kreisradius (R). Somit,

Nach dem Multiplizieren beider Seiten der Gleichung mit A ** 2+1wir bekommen:

Nachdem wir alles auf eine Seite verschoben und die Gleichung auf Null gesetzt haben, erhalten wir:

Da wir zwei Kreise haben und eine Tangente für beide finden müssen, haben wir das folgende Gleichungssystem:

Dies funktioniert großartig, aber das Downside ist, dass wir in der Realität 4 mögliche Tangentenlinien haben:

Und wir müssen nur 2 von ihnen wählen – externe.
Zu diesem Zweck müssen wir jede Tangente und jeden Kreiszentrum überprüfen und feststellen, ob die Linie über oder unter dem Punkt liegt:

Wir brauchen die beiden Linien, die beide über die Zentren der Kreise passieren oder beide unter den Zentren der Kreise.
Lassen Sie uns jetzt alle diese Schritte in Code übersetzen:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import sympy as sp
from scipy.spatial import ConvexHull
import math
from matplotlib import rcParams
import matplotlib.patches as patches
def check_position_relative_to_line(a, b, x0, y0):
y_line = a * x0 + b
if y0 > y_line:
return 1 # line is above the purpose
elif y0 < y_line:
return -1
def find_tangent_equations(x1, y1, r1, x2, y2, r2):
a, b = sp.symbols('a b')
tangent_1 = (a*x1 + b - y1)**2 - r1**2 * (a**2 + 1)
tangent_2 = (a*x2 + b - y2)**2 - r2**2 * (a**2 + 1)
eqs_1 = (tangent_2, tangent_1)
resolution = sp.resolve(eqs_1, (a, b))
parameters = ((float(e(0)), float(e(1))) for e in resolution)
# filter simply exterior tangents
parameters_filtered = ()
for tangent in parameters:
a = tangent(0)
b = tangent(1)
if abs(check_position_relative_to_line(a, b, x1, y1) + check_position_relative_to_line(a, b, x2, y2)) == 2:
parameters_filtered.append(tangent)
return parameters_filteredJetzt müssen wir nur noch die Schnittpunkte der Tangenten mit den Kreisen finden. Diese 4 Punkte sind die Eckpunkte des gewünschten Polygons.
Kreisgleichung:

Ersetzen Sie die Liniengleichung y = ax+b in die Kreisgleichung:

Lösung der Gleichung ist die X der Kreuzung.
Dann berechnen y Aus der Liniengleichung:

Wie es sich in den Code übersetzt:
def find_circle_line_intersection(circle_x, circle_y, circle_r, line_a, line_b):
x, y = sp.symbols('x y')
circle_eq = (x - circle_x)**2 + (y - circle_y)**2 - circle_r**2
intersection_eq = circle_eq.subs(y, line_a * x + line_b)
sol_x_raw = sp.resolve(intersection_eq, x)(0)
strive:
sol_x = float(sol_x_raw)
besides:
sol_x = sol_x_raw.as_real_imag()(0)
sol_y = line_a * sol_x + line_b
return sol_x, sol_yJetzt möchten wir Beispieldaten generieren, um die gesamten Diagrammzusammensetzungen zu demonstrieren.
Stellen Sie sich vor, wir haben 4 Benutzer auf unserer Plattform. Wir wissen, wie viele Einkäufe sie getätigt und auf der Plattform Einnahmen und Aktivitäten erzielt haben. Alle diese Metriken werden für 2 Zeiträume berechnet (nennen wir sie vor und nach der Zeit).
# knowledge technology
df = pd.DataFrame({'person': ('Emily', 'Emily', 'James', 'James', 'Tony', 'Tony', 'Olivia', 'Olivia'),
'interval': ('pre', 'put up', 'pre', 'put up', 'pre', 'put up', 'pre', 'put up'),
'num_purchases': (10, 9, 3, 5, 2, 4, 8, 7),
'income': (70, 60, 80, 90, 20, 15, 80, 76),
'exercise': (100, 80, 50, 90, 210, 170, 60, 55)})
Nehmen wir an, dass „Aktivität“ der Bereich der Blase ist. Lassen Sie uns nun in den Radius der Blase umwandeln. Wir werden auch die Y-Achse skalieren.
def area_to_radius(space):
radius = math.sqrt(space / math.pi)
return radius
x_alias, y_alias, a_alias="num_purchases", 'income', 'exercise'
# scaling metrics
radius_scaler = 0.1
df('radius') = df(a_alias).apply(area_to_radius) * radius_scaler
df('y_scaled') = df(y_alias) / df(x_alias).max()Erstellen wir nun das Diagramm – 2 Kreise und das Polygon.
def draw_polygon(plt, factors):
hull = ConvexHull(factors)
convex_points = (factors(i) for i in hull.vertices)
x, y = zip(*convex_points)
x += (x(0),)
y += (y(0),)
plt.fill(x, y, colour="#99d8e1", alpha=1, zorder=1)
# bubble pre
for _, row in df(df.interval=='pre').iterrows():
x = row(x_alias)
y = row.y_scaled
r = row.radius
circle = patches.Circle((x, y), r, facecolor="#99d8e1", edgecolor="none", linewidth=0, zorder=2)
plt.gca().add_patch(circle)
# transition space
for person in df.person.distinctive():
user_pre = df((df.person==person) & (df.interval=='pre'))
x1, y1, r1 = user_pre(x_alias).values(0), user_pre.y_scaled.values(0), user_pre.radius.values(0)
user_post = df((df.person==person) & (df.interval=='put up'))
x2, y2, r2 = user_post(x_alias).values(0), user_post.y_scaled.values(0), user_post.radius.values(0)
tangent_equations = find_tangent_equations(x1, y1, r1, x2, y2, r2)
circle_1_line_intersections = (find_circle_line_intersection(x1, y1, r1, eq(0), eq(1)) for eq in tangent_equations)
circle_2_line_intersections = (find_circle_line_intersection(x2, y2, r2, eq(0), eq(1)) for eq in tangent_equations)
polygon_points = circle_1_line_intersections + circle_2_line_intersections
draw_polygon(plt, polygon_points)
# bubble put up
for _, row in df(df.interval=='put up').iterrows():
x = row(x_alias)
y = row.y_scaled
r = row.radius
label = row.person
circle = patches.Circle((x, y), r, facecolor="#2d699f", edgecolor="none", linewidth=0, zorder=2)
plt.gca().add_patch(circle)
plt.textual content(x, y - r - 0.3, label, fontsize=12, ha="heart")Die Ausgabe sieht wie erwartet aus:

Jetzt möchten wir etwas Styling hinzufügen:
# plot parameters
plt.subplots(figsize=(10, 10))
rcParams('font.household') = 'DejaVu Sans'
rcParams('font.measurement') = 14
plt.grid(colour="grey", linestyle=(0, (10, 10)), linewidth=0.5, alpha=0.6, zorder=1)
plt.axvline(x=0, colour="white", linewidth=2)
plt.gca().set_facecolor('white')
plt.gcf().set_facecolor('white')
# spines formatting
plt.gca().spines("high").set_visible(False)
plt.gca().spines("proper").set_visible(False)
plt.gca().spines("backside").set_visible(False)
plt.gca().spines("left").set_visible(False)
plt.gca().tick_params(axis="each", which="each", size=0)
# plot labels
plt.xlabel("Quantity purchases")
plt.ylabel("Income, $")
plt.title("Product customers efficiency", fontsize=18, colour="black")
# axis limits
axis_lim = df(x_alias).max() * 1.2
plt.xlim(0, axis_lim)
plt.ylim(0, axis_lim)PRO-POST-Legende in der rechten unteren Ecke, um den Betrachter einen Hinweis zu geben, wie Sie das Diagramm lesen:
## pre-post legend
# circle 1
legend_position, r1 = (11, 2.2), 0.3
x1, y1 = legend_position(0), legend_position(1)
circle = patches.Circle((x1, y1), r1, facecolor="#99d8e1", edgecolor="none", linewidth=0, zorder=2)
plt.gca().add_patch(circle)
plt.textual content(x1, y1 + r1 + 0.15, 'Pre', fontsize=12, ha="heart", va="heart")
# circle 2
x2, y2 = legend_position(0), legend_position(1) - r1*3
r2 = r1*0.7
circle = patches.Circle((x2, y2), r2, facecolor="#2d699f", edgecolor="none", linewidth=0, zorder=2)
plt.gca().add_patch(circle)
plt.textual content(x2, y2 - r2 - 0.15, 'Submit', fontsize=12, ha="heart", va="heart")
# tangents
tangent_equations = find_tangent_equations(x1, y1, r1, x2, y2, r2)
circle_1_line_intersections = (find_circle_line_intersection(x1, y1, r1, eq(0), eq(1)) for eq in tangent_equations)
circle_2_line_intersections = (find_circle_line_intersection(x2, y2, r2, eq(0), eq(1)) for eq in tangent_equations)
polygon_points = circle_1_line_intersections + circle_2_line_intersections
draw_polygon(plt, polygon_points)
# small arrow
plt.annotate('', xytext=(x1, y1), xy=(x2, y1 - r1*2), arrowprops=dict(edgecolor="black", arrowstyle="->", lw=1))
Und schließlich die Legende der Blasengröße:
# bubble measurement legend
legend_areas_original = (150, 50)
legend_position = (11, 10.2)
for i in legend_areas_original:
i_r = area_to_radius(i) * radius_scaler
circle = plt.Circle((legend_position(0), legend_position(1) + i_r), i_r, colour="black", fill=False, linewidth=0.6, facecolor="none")
plt.gca().add_patch(circle)
plt.textual content(legend_position(0), legend_position(1) + 2*i_r, str(i), fontsize=12, ha="heart", va="heart",
bbox=dict(facecolor="white", edgecolor="none", boxstyle="spherical,pad=0.1"))
legend_label_r = area_to_radius(np.max(legend_areas_original)) * radius_scaler
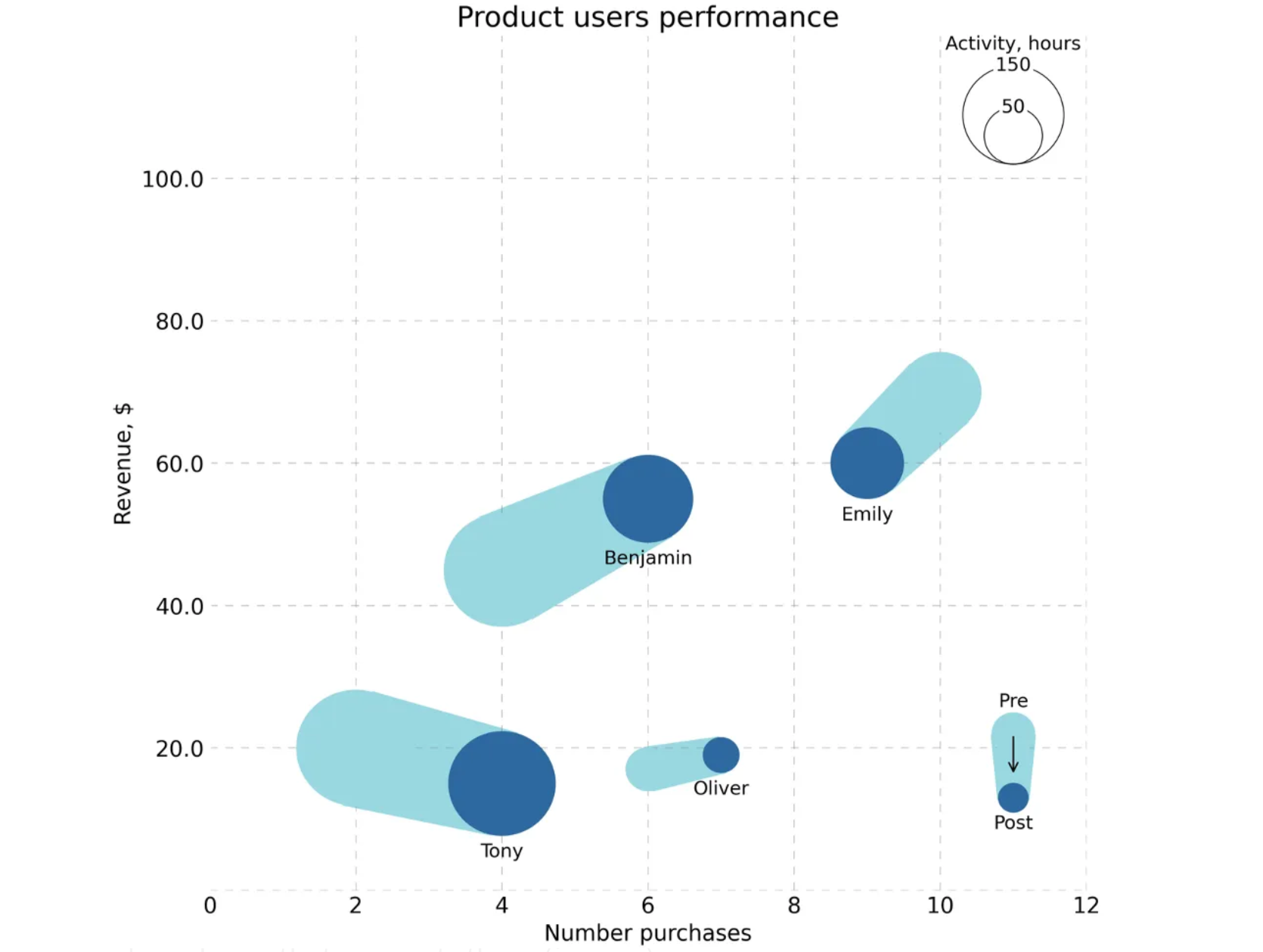
plt.textual content(legend_position(0), legend_position(1) + 2*legend_label_r + 0.3, 'Exercise, hours', fontsize=12, ha="heart", va="heart")Unsere letzte Tabelle sieht so aus:

Die Visualisierung sieht sehr stilvoll aus und konzentriert sich in kompakter Type ziemlich viel Informationen.
Hier ist der vollständige Code für die Grafik:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import sympy as sp
from scipy.spatial import ConvexHull
import math
from matplotlib import rcParams
import matplotlib.patches as patches
def check_position_relative_to_line(a, b, x0, y0):
y_line = a * x0 + b
if y0 > y_line:
return 1 # line is above the purpose
elif y0 < y_line:
return -1
def find_tangent_equations(x1, y1, r1, x2, y2, r2):
a, b = sp.symbols('a b')
tangent_1 = (a*x1 + b - y1)**2 - r1**2 * (a**2 + 1)
tangent_2 = (a*x2 + b - y2)**2 - r2**2 * (a**2 + 1)
eqs_1 = (tangent_2, tangent_1)
resolution = sp.resolve(eqs_1, (a, b))
parameters = ((float(e(0)), float(e(1))) for e in resolution)
# filter simply exterior tangents
parameters_filtered = ()
for tangent in parameters:
a = tangent(0)
b = tangent(1)
if abs(check_position_relative_to_line(a, b, x1, y1) + check_position_relative_to_line(a, b, x2, y2)) == 2:
parameters_filtered.append(tangent)
return parameters_filtered
def find_circle_line_intersection(circle_x, circle_y, circle_r, line_a, line_b):
x, y = sp.symbols('x y')
circle_eq = (x - circle_x)**2 + (y - circle_y)**2 - circle_r**2
intersection_eq = circle_eq.subs(y, line_a * x + line_b)
sol_x_raw = sp.resolve(intersection_eq, x)(0)
strive:
sol_x = float(sol_x_raw)
besides:
sol_x = sol_x_raw.as_real_imag()(0)
sol_y = line_a * sol_x + line_b
return sol_x, sol_y
def draw_polygon(plt, factors):
hull = ConvexHull(factors)
convex_points = (factors(i) for i in hull.vertices)
x, y = zip(*convex_points)
x += (x(0),)
y += (y(0),)
plt.fill(x, y, colour="#99d8e1", alpha=1, zorder=1)
def area_to_radius(space):
radius = math.sqrt(space / math.pi)
return radius
# knowledge technology
df = pd.DataFrame({'person': ('Emily', 'Emily', 'James', 'James', 'Tony', 'Tony', 'Olivia', 'Olivia', 'Oliver', 'Oliver', 'Benjamin', 'Benjamin'),
'interval': ('pre', 'put up', 'pre', 'put up', 'pre', 'put up', 'pre', 'put up', 'pre', 'put up', 'pre', 'put up'),
'num_purchases': (10, 9, 3, 5, 2, 4, 8, 7, 6, 7, 4, 6),
'income': (70, 60, 80, 90, 20, 15, 80, 76, 17, 19, 45, 55),
'exercise': (100, 80, 50, 90, 210, 170, 60, 55, 30, 20, 200, 120)})
x_alias, y_alias, a_alias="num_purchases", 'income', 'exercise'
# scaling metrics
radius_scaler = 0.1
df('radius') = df(a_alias).apply(area_to_radius) * radius_scaler
df('y_scaled') = df(y_alias) / df(x_alias).max()
# plot parameters
plt.subplots(figsize=(10, 10))
rcParams('font.household') = 'DejaVu Sans'
rcParams('font.measurement') = 14
plt.grid(colour="grey", linestyle=(0, (10, 10)), linewidth=0.5, alpha=0.6, zorder=1)
plt.axvline(x=0, colour="white", linewidth=2)
plt.gca().set_facecolor('white')
plt.gcf().set_facecolor('white')
# spines formatting
plt.gca().spines("high").set_visible(False)
plt.gca().spines("proper").set_visible(False)
plt.gca().spines("backside").set_visible(False)
plt.gca().spines("left").set_visible(False)
plt.gca().tick_params(axis="each", which="each", size=0)
# plot labels
plt.xlabel("Quantity purchases")
plt.ylabel("Income, $")
plt.title("Product customers efficiency", fontsize=18, colour="black")
# axis limits
axis_lim = df(x_alias).max() * 1.2
plt.xlim(0, axis_lim)
plt.ylim(0, axis_lim)
# bubble pre
for _, row in df(df.interval=='pre').iterrows():
x = row(x_alias)
y = row.y_scaled
r = row.radius
circle = patches.Circle((x, y), r, facecolor="#99d8e1", edgecolor="none", linewidth=0, zorder=2)
plt.gca().add_patch(circle)
# transition space
for person in df.person.distinctive():
user_pre = df((df.person==person) & (df.interval=='pre'))
x1, y1, r1 = user_pre(x_alias).values(0), user_pre.y_scaled.values(0), user_pre.radius.values(0)
user_post = df((df.person==person) & (df.interval=='put up'))
x2, y2, r2 = user_post(x_alias).values(0), user_post.y_scaled.values(0), user_post.radius.values(0)
tangent_equations = find_tangent_equations(x1, y1, r1, x2, y2, r2)
circle_1_line_intersections = (find_circle_line_intersection(x1, y1, r1, eq(0), eq(1)) for eq in tangent_equations)
circle_2_line_intersections = (find_circle_line_intersection(x2, y2, r2, eq(0), eq(1)) for eq in tangent_equations)
polygon_points = circle_1_line_intersections + circle_2_line_intersections
draw_polygon(plt, polygon_points)
# bubble put up
for _, row in df(df.interval=='put up').iterrows():
x = row(x_alias)
y = row.y_scaled
r = row.radius
label = row.person
circle = patches.Circle((x, y), r, facecolor="#2d699f", edgecolor="none", linewidth=0, zorder=2)
plt.gca().add_patch(circle)
plt.textual content(x, y - r - 0.3, label, fontsize=12, ha="heart")
# bubble measurement legend
legend_areas_original = (150, 50)
legend_position = (11, 10.2)
for i in legend_areas_original:
i_r = area_to_radius(i) * radius_scaler
circle = plt.Circle((legend_position(0), legend_position(1) + i_r), i_r, colour="black", fill=False, linewidth=0.6, facecolor="none")
plt.gca().add_patch(circle)
plt.textual content(legend_position(0), legend_position(1) + 2*i_r, str(i), fontsize=12, ha="heart", va="heart",
bbox=dict(facecolor="white", edgecolor="none", boxstyle="spherical,pad=0.1"))
legend_label_r = area_to_radius(np.max(legend_areas_original)) * radius_scaler
plt.textual content(legend_position(0), legend_position(1) + 2*legend_label_r + 0.3, 'Exercise, hours', fontsize=12, ha="heart", va="heart")
## pre-post legend
# circle 1
legend_position, r1 = (11, 2.2), 0.3
x1, y1 = legend_position(0), legend_position(1)
circle = patches.Circle((x1, y1), r1, facecolor="#99d8e1", edgecolor="none", linewidth=0, zorder=2)
plt.gca().add_patch(circle)
plt.textual content(x1, y1 + r1 + 0.15, 'Pre', fontsize=12, ha="heart", va="heart")
# circle 2
x2, y2 = legend_position(0), legend_position(1) - r1*3
r2 = r1*0.7
circle = patches.Circle((x2, y2), r2, facecolor="#2d699f", edgecolor="none", linewidth=0, zorder=2)
plt.gca().add_patch(circle)
plt.textual content(x2, y2 - r2 - 0.15, 'Submit', fontsize=12, ha="heart", va="heart")
# tangents
tangent_equations = find_tangent_equations(x1, y1, r1, x2, y2, r2)
circle_1_line_intersections = (find_circle_line_intersection(x1, y1, r1, eq(0), eq(1)) for eq in tangent_equations)
circle_2_line_intersections = (find_circle_line_intersection(x2, y2, r2, eq(0), eq(1)) for eq in tangent_equations)
polygon_points = circle_1_line_intersections + circle_2_line_intersections
draw_polygon(plt, polygon_points)
# small arrow
plt.annotate('', xytext=(x1, y1), xy=(x2, y1 - r1*2), arrowprops=dict(edgecolor="black", arrowstyle="->", lw=1))
# y axis formatting
max_y = df(y_alias).max()
nearest_power_of_10 = 10 ** math.ceil(math.log10(max_y))
ticks = (spherical(nearest_power_of_10/5 * i, 2) for i in vary(0, 6))
yticks_scaled = ticks / df(x_alias).max()
yticklabels = (str(i) for i in ticks)
yticklabels(0) = ''
plt.yticks(yticks_scaled, yticklabels)
plt.savefig("plot_with_white_background.png", bbox_inches="tight", dpi=300)Das Hinzufügen einer Zeitdimension zu Blasendiagrammen verbessert ihre Fähigkeit, dynamische Daten intuitiv zu vermitteln. Durch die Implementierung von reibungslosen Übergängen zwischen „vor“ und „Nachher“ -Staaten können Benutzer Developments und Vergleiche im Laufe der Zeit besser verstehen.
Während keine fertigen Lösungen verfügbar waren, erwies sich die Entwicklung eines benutzerdefinierten Ansatzes sowohl herausfordernd als auch lohnend, was mathematische Erkenntnisse und sorgfältige Animationstechniken erforderte. Die vorgeschlagene Methode kann leicht auf verschiedene Datensätze erweitert werden, was es zu einem wertvollen Device für Datenvisualisierung in Wirtschaft, Wissenschaft und Analytik.