Einführung in die Log-Normalverteilung

Einführung

Die logarithmische Normalverteilung ist ein faszinierendes statistisches Konzept, das häufig zur Modellierung von Daten mit rechtsschiefem Verhalten verwendet wird. Diese Verteilung hat vielfältige Anwendungsmöglichkeiten in verschiedenen Bereichen wie Biologie, Finanzen und Ingenieurwesen. In diesem Artikel werden wir uns eingehend mit der logarithmischen Normalverteilung, ihren wichtigsten Parametern und ihrer Interpretation befassen und einige praktische Beispiele zum besseren Verständnis untersuchen.

Überblick

• Eine Log-Normalverteilung modelliert Daten, bei denen der natürliche Logarithmus einer Variablen einer Normalverteilung folgt und eine optimistic Schiefe aufweist.
• Verstehen Sie die Parameter Kind (σ), Maßstab (m oder eμ) und Lage (μ), um die logarithmische Normalverteilung zu interpretieren und anzuwenden.
• Die Log-Normalverteilung ist mit der Normalverteilung verbunden; wenn X log-normal verteilt ist, ist ln(X) normalerweise verteilt und umgekehrt.
• Schätzen Sie die Parameter μ σ aus den Daten mithilfe von Techniken wie der Most-Chance-Schätzung, die eine Log-Transformation und die Berechnung des Mittelwerts und der Standardabweichung umfasst.
• Die logarithmische Normalverteilung wird in der Biologie, im Finanzwesen, in der Zuverlässigkeitstechnik und in den Umweltwissenschaften häufig verwendet, um rechtsschiefe Daten wie Wachstumsraten, Aktienkurse und Zeitspannen bis zum Ausfall zu modellieren.

Was ist eine Log-Normalverteilung?

Eine Log-Normalverteilung beschreibt die Wahrscheinlichkeitsverteilung einer Zufallsvariablen, wenn ihr Logarithmus einer Normalverteilung folgt. Einfacher ausgedrückt: Wenn der natürliche Logarithmus einer Variable X einer Normalverteilung folgt, dann folgt X einer logarithmischen Normalverteilung. Diese Verteilung bleibt kontinuierlich und weist eine optimistic Schiefe auf, was bedeutet, dass sie einen langen rechten Rand hat.

Schlüsselparameter

Es gibt im Wesentlichen die folgenden drei Parameter:

1. Formparameter (σ): Dieser Parameter beeinflusst die allgemeine Kind der Verteilung. Er ist zugleich die Standardabweichung der logarithmisch transformierten Variable.
2. Skalierungsparameter (m oder tμ): Dieser Parameter streckt oder verkleinert den Graphen der Verteilung. In dieser Verteilung wird der Skalenparameter oft als Median bezeichnet.
3. Standortparameter (μ): Dieser Parameter bestimmt, wo auf der x-Achse sich das Diagramm befindet. Es handelt sich um den Mittelwert der logarithmisch transformierten Variablen.

Diese Parameter sind entscheidend für das Verständnis des Verhaltens dieser Verteilung und ihrer Anwendbarkeit auf reale Daten.

Lesen Sie auch: Was ist Normalverteilung: Ein ultimativer Leitfaden

Wahrscheinlichkeitsdichtefunktion

Der Wahrscheinlichkeitsdichtefunktion (PDF) einer lognormalen Verteilung ist gegeben durch:

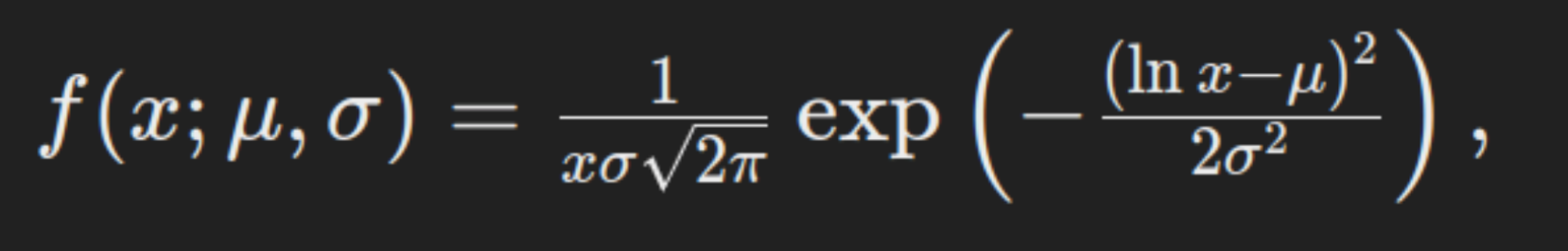
wobei x>0, μ der Mittelwert des Logarithmus der Variablen ist und σ ist die Standardabweichung des Logarithmus der Variablen. Diese Formel zeigt, dass die Lognormalverteilung nur für optimistic Werte definiert ist, da der Logarithmus für nicht optimistic Werte nicht definiert ist.

Beziehung zur Normalverteilung

Einer der interessantesten Aspekte seiner Beziehung zur Normalverteilung. Wenn X einer logarithmischen Normalverteilung folgt, folgt Y = ln(X) einer Normalverteilung. Umgekehrt, wenn Y einer Normalverteilung folgt, ist X = eY folgt einer logarithmischen Normalverteilung. Diese Beziehung ermöglicht es uns, bewährte Methoden für Normalverteilungen zu verwenden, um logarithmisch verteilte Daten zu analysieren, indem wir die Daten mithilfe von Logarithmen transformieren.

Berechnen von Parametern aus Daten

Wir verwenden häufig Methoden wie Most-Chance-Schätzung (MLE) um die Parameter von t abzuschätzenseine Kind von Verteilung aus Daten. Hier ist ein vereinfachter Ansatz zur Schätzung von μ und σ:

1. Log-Transformation der Daten: Nehmen Sie den natürlichen Logarithmus aller Datenpunkte.
2. Berechnen Sie den Stichprobenmittelwert und die Standardabweichung der logarithmisch transformierten Daten: Diese Statistiken stellen die Schätzungen für μ und σ dar.

Betrachten wir beispielsweise einen Datensatz logarithmisch normalverteilter Einkommen. Indem wir den natürlichen Logarithmus jedes Einkommens nehmen, können wir den Mittelwert und die Standardabweichung dieser logarithmisch transformierten Werte berechnen, um μ und σ abzuschätzen.

Praktische Anwendungen

Diese Verteilung wird aufgrund ihrer Fähigkeit, verzerrte Daten zu modellieren, in verschiedenen Bereichen häufig verwendet. Hier sind einige Beispiele:

1. Biologie: In biologischen Studien folgen die Wachstumsraten von Organismen häufig einer logarithmischen Normalverteilung, da diese eher multiplikativ als additiv sind.
2. Finanzen: Aktienkurse werden üblicherweise mithilfe logarithmischer Normalverteilungen modelliert, da die prozentuale Preisänderung regular verteilt ist.
3. Zuverlässigkeitstechnik: Die Zeit bis zum Ausfall bestimmter Produkte kann mithilfe einer logarithmischen Normalverteilung modelliert werden, insbesondere wenn der Ausfallprozess multiplikativ ist.
4. Umweltwissenschaft: Die Verteilung der Partikelgröße in Aerosolen oder die Niederschlagsmenge in einem bestimmten Zeitraum.

Beispielberechnung

Betrachten wir ein praktisches Beispiel zur Berechnung der Parameter einer logarithmischen Normalverteilung. Angenommen, wir haben die folgenden Einkommensdaten (in Tausend): 20, 22, 25, 27, 30.

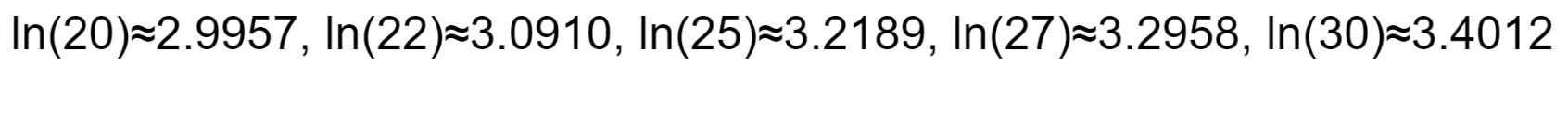
• Berechnen des Stichprobenmittelwerts μ:

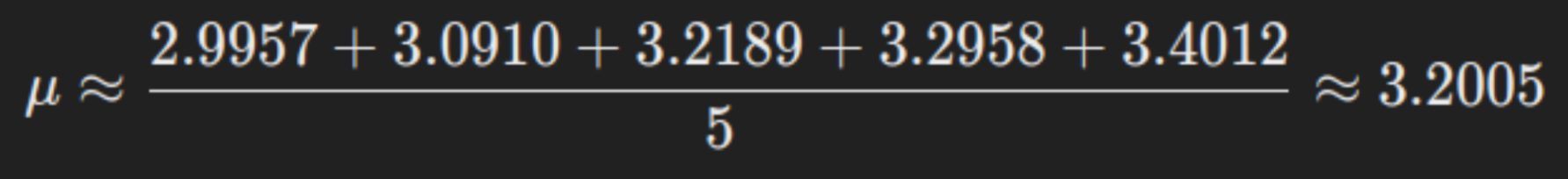
• Berechnen Sie die Stichprobenstandardabweichung (σ):

Somit betragen die geschätzten Parameter für die logarithmische Normalverteilung μ ca. 3,2005 und σ ca. 0,1504.

Interpretieren der Parameter

• μ: Dies ist der Mittelwert der logarithmisch transformierten Daten. In unserem Beispiel bedeutet ein μ von 3,2005, dass der Durchschnitt der natürlichen Logarithmen der Einkommen bei diesem Wert liegt.
• σ: Dies ist die Standardabweichung der logarithmisch transformierten Daten. Ein σ von 0,1504 deutet darauf hin, dass die logarithmisch transformierten Einkommen auf einer logarithmischen Skala relativ nahe am Mittelwert liegen.

Abschluss

Die logarithmische Normalverteilung ist ein leistungsfähiges Werkzeug zur Modellierung rechtsschiefer Daten. Wir können Daten in verschiedenen Bereichen effektiv analysieren und interpretieren, indem wir ihre Schlüsselparameter und ihre Beziehung zur Normalverteilung verstehen. Ob es sich nun um Finanzdaten, biologische Wachstumsraten oder Zuverlässigkeitsmetriken handelt, sie bietet einen robusten Rahmen zum Verständnis und zur Vorhersage von Verhalten.

Häufig gestellte Fragen