Python Monte Carlo Simulation in Excel

In unserem daten dominierten finanziellen Umfeld ist die Monte-Carlo-Simulation ein wichtiges Instrument zur Risikomodellierung und quantitativen Strategien. Viele von uns werden Excel weiterhin als bevorzugte Plattform verwenden, aber es ist bedauerlich, dass Excels Grundfunktionen die zusätzliche Arbeit erfordern, die viele Finanzfachleute für jede stochastische Modellierung abschließen müssen. In diesem Handbuch zeigen wir Ihnen, wie Sie eine Monte -Carlo -Simulation in Python in Excel „anschließen“ können, um eine hybride Optimierung für die fortschrittliche Risikoanalyse und die Finanzmodellierung zu entwickeln.

Verständnis der Monte -Carlo -Simulation im Risikomanagement

Die Monte -Carlo -Simulation führt durch Ausführung von Tausenden oder Millionen von zufälligen Realisierungen, wobei die anfänglichen Eingangsvariablen durch Wahrscheinlichkeitsverteilungen definiert sind. Der probabilistische Modellierungsansatz bietet in Situationen unsicherer Ergebnisse und finanzielles Risikomanagement mehrere Vorteile.

Die Methodik definiert Wahrscheinlichkeitsverteilungen für unsichere Variablen, erzeugt zufällige Variationen, führt Berechnungen für jede Realisierung durch und bewertet statistische Ergebnisse. Die Monte -Carlo -Simulation bietet Einblicke, die über deterministische Modelle hinausgehen und sich als besonders nützlich für die Portfolio -Optimierung und die Kreditrisikomodellierung als nützlich erweisen.

Risikokennzahlen wie Worth-at-Risiko (VAR), erwarteter Mangel und Verlustwahrscheinlichkeit können mit der Monte-Carlo-Schätzung geschätzt werden. Monte-Carlo-Techniken bieten Analysten eine maximale Flexibilität, um komplexe Korrelationen über Variablen hinweg zu modellieren, nicht normale Verteilungen zu verwenden und zeitabhängige Parameter im Einklang mit den Stay-Marktbedingungen zu berücksichtigen.

Python -Bibliotheken für die Monte -Carlo -Risikomodellierung

Viele Python -Bibliotheken unterstützen eine herausragende Unterstützung für die Monte -Carlo -Simulation und die statistische Analyse:

1. Numpy: Numpy ist das Rückgrat aufgrund seiner leistungsstarken Array -Operationen und der Zufallszahlenerzeugung. Es führt vektorisierte Operationen durch und ermöglicht effiziente groß angelegte Simulationen. Die Bibliothek bietet auch viele statistische Funktionen für Wahrscheinlichkeitsverteilungen in der Finanzmodellierung.
2. Scipy: Scipy baut auf Numpy mit statistischen Verteilungen und Optimierungsalgorithmen auf. Es bietet über 80 Verteilungen und Assessments zur Risikomodellierung. Scipy unterstützt auch komplexe Finanzanwendungen durch numerische Integrationsmethoden.
3. Pandas: Pandas ist sehr nützlich für die Datenmanipulation und die Zeitreihenanalyse. Der DataFrame integriert sich reibungslos in Excel durch verschiedene Import- und Exportfunktionen, wodurch die Analyse der Finanzdaten und die Aggregation einfacher wird.
4. Matplotlib Und Seeborn: Matplotlib und Seeborn ermöglichen Datenvisualisierungen von Simulationsergebnissen in professioneller Qualität. Diese Visualisierungen können Risikoverteilungen oder Sensitivitätsanalysen umfassen, die in Excel -Berichte eingebettet werden können.

Excel-Integrationsstrategien: Python-Excel-Konnektivität

Es gibt mehrere moderne Optionen für Excel -Python -Integrationsoptionen und sie haben unterschiedliche Stärken für die Monte -Carlo -Risikomodellierung:

1. Xlwings ist die nahtloses Integrationsoption. Diese Bibliothek ermöglicht die bidirektionale Kommunikation zwischen Excel und Python und unterstützt die Stay-Datenaustausch- und Echtzeit-Simulationsergebnisse.
2. openpyxl Und XLSXWriter Beide bieten eine großartige dateibasierte Integrationsoption, die nicht verwendet werden kann, wenn keine direkte Verbindung erforderlich ist. Mit dieser Bibliothek ermöglichen es, komplexe Berichte zu erstellen, mehrere Arbeitsblätter, Formatierung und Diagramme in Excel aus Python -Simulationen zu bewältigen. Jede Bibliothek kann den Job machen.
3. Com Automatisierung mit Pywin32 Ermöglicht eine tiefe Integration von Excel auf Home windows -Maschinen, da die Bibliothek die Erstellung und Manipulation von Excel -Objekten, -Rang und -Andabellen automatisiert. Diese Possibility kann von Vorteil sein, wenn Sie anspruchsvolle Risiko -Dashboards und interaktive Modellierungsumgebungen erstellen möchten.

Praktische Implementierung: Aufbau eines Monte-Carlo-Risikomodells

Es ist Zeit, ein robustes Portfolio -Risikoanalyse -System zu erstellen Excel und a Python Monte Carlo Simulation. Anhand dieses praktischen Beispiels werden wir Aktienkursprognose, Korrelationsanalyse und Berechnung von Risikokennzahlen nachweisen.

1. Richten Sie die Python -Umgebung ein und bereiten Sie die Daten vor.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
from datetime import datetime, timedelta
import warnings
warnings.filterwarnings('ignore')

# Portfolio configuration
shares = ('AAPL', 'GOOGL', 'MSFT', 'AMZN', 'TSLA')
initial_portfolio_value = 1_000_000
time_horizon = 252
num_simulations = 10000

np.random.seed(42)
annual_returns = np.array((0.15, 0.12, 0.14, 0.18, 0.25))
annual_volatilities = np.array((0.25, 0.22, 0.24, 0.28, 0.35))
portfolio_weights = np.array((0.25, 0.20, 0.25, 0.15, 0.15))

correlation_matrix = np.array((
    (1.00, 0.65, 0.72, 0.58, 0.45),
    (0.65, 1.00, 0.68, 0.62, 0.38),
    (0.72, 0.68, 1.00, 0.55, 0.42),
    (0.58, 0.62, 0.55, 1.00, 0.48),
    (0.45, 0.38, 0.42, 0.48, 1.00)
))

2. Monte Carlo Simulationsmotor

def monte_carlo_portfolio_simulation(returns, volatilities, correlation_matrix,
                                     weights, initial_value, time_horizon, num_sims):
    # Convert annual parameters to every day
    daily_returns = returns / 252
    daily_volatilities = volatilities / np.sqrt(252)

    # Generate correlated random returns
    L = np.linalg.cholesky(correlation_matrix)

    # Storage for simulation outcomes
    portfolio_values = np.zeros((num_sims, time_horizon + 1))
    portfolio_values(:, 0) = initial_value

    # Run Monte Carlo simulation
    for sim in vary(num_sims):
        random_shocks = np.random.regular(0, 1, (time_horizon, len(shares)))
        correlated_shocks = random_shocks @ L.T

        daily_asset_returns = daily_returns + daily_volatilities * correlated_shocks
        portfolio_daily_returns = np.sum(daily_asset_returns * weights, axis=1)

        for day in vary(time_horizon):
            portfolio_values(sim, day + 1) = portfolio_values(sim, day) * (1 + portfolio_daily_returns(day))

    return portfolio_values

# Execute simulation
print("Working Monte Carlo simulation...")
simulation_results = monte_carlo_portfolio_simulation(
    annual_returns, annual_volatilities, correlation_matrix,
    portfolio_weights, initial_portfolio_value, time_horizon, num_simulations
)

3. Berechnung und Analyse von Risikometriken

def calculate_risk_metrics(portfolio_values, confidence_levels=(0.95, 0.99)):
    final_values = portfolio_values(:, -1)
    returns = (final_values - portfolio_values(:, 0)) / portfolio_values(:, 0)
    losses = -returns

    mean_return = np.imply(returns)
    volatility = np.std(returns)

    # VaR
    var_metrics = {}
    for confidence in confidence_levels:
        var_metrics(f'VaR_{int(confidence*100)}%') = np.percentile(losses, confidence * 100)

    # Anticipated Shortfall
    es_metrics = {}
    for confidence in confidence_levels:
        threshold = np.percentile(losses, confidence * 100)
        es_metrics(f'ES_{int(confidence*100)}%') = np.imply(losses(losses >= threshold))

    max_loss = np.max(losses)
    prob_loss = np.imply(returns < 0)
    sharpe_ratio = mean_return / volatility if volatility > 0 else 0

    return {
        'mean_return': mean_return,
        'volatility': volatility,
        'sharpe_ratio': sharpe_ratio,
        'max_loss': max_loss,
        'prob_loss': prob_loss,
        **var_metrics,
        **es_metrics
    }

risk_metrics = calculate_risk_metrics(simulation_results)

4. Excel -Integration und Dashboard -Erstellung

def create_excel_risk_dashboard(simulation_results, risk_metrics, shares, weights):
    portfolio_data = pd.DataFrame({
        "Inventory": shares,
        "Weight": weights,
        "Anticipated Return": annual_returns,
        "Volatility": annual_volatilities
    })

    metrics_df = pd.DataFrame(checklist(risk_metrics.objects()), columns=('Metric', 'Worth'))
    metrics_df('Worth') = metrics_df('Worth').spherical(4)

    final_values = simulation_results(:, -1)
    # Excel export code would observe right here

summary_stats = {
    "Preliminary Portfolio Worth": f"${initial_portfolio_value:,.0f}",
    "Imply Ultimate Worth": f"${np.imply(final_values):,.0f}",
    "Median Ultimate Worth": f"${np.median(final_values):,.0f}",
    "Commonplace Deviation": f"${np.std(final_values):,.0f}",
    "Minimal Worth": f"${np.min(final_values):,.0f}",
    "Most Worth": f"${np.max(final_values):,.0f}"
}

summary_df = pd.DataFrame(checklist(summary_stats.objects()), columns=('Statistic', 'Worth'))

plt.determine(figsize=(10, 6))
plt.hist(final_values, bins=50, alpha=0.7, colour="skyblue", edgecolor="black")

plt.axvline(initial_portfolio_value, colour="crimson", linestyle="--",
            label=f'Preliminary Worth: ${initial_portfolio_value:,.0f}')
plt.axvline(np.imply(final_values), colour="inexperienced", linestyle="--",
            label=f'Imply Ultimate Worth: ${np.imply(final_values):,.0f}')

var_95 = initial_portfolio_value * (1 - risk_metrics('VaR_95%'))
plt.axvline(var_95, colour="orange", linestyle="--",
            label=f'95% VaR: ${var_95:,.0f}')

plt.title("Portfolio Worth Distribution - Monte Carlo Simulation")
plt.xlabel("Portfolio Worth ($)")
plt.ylabel("Frequency")
plt.legend()
plt.grid(True, alpha=0.3)
plt.savefig("portfolio_distribution.png", dpi=300, bbox_inches="tight")
plt.shut()

5. Superior Szenarioanalyse

def scenario_stress_testing(base_returns, base_volatilities,             correlation_matrix, weights, initial_value, situations):
    scenario_results = {}
    for scenario_name, (return_shock, vol_shock) in situations.objects():
        stressed_returns = base_returns + return_shock
        stressed_volatilities = base_volatilities * (1 + vol_shock)

        scenario_sim = monte_carlo_portfolio_simulation(
            stressed_returns, stressed_volatilities, correlation_matrix,
            weights, initial_value, time_horizon, 5000
        )

        scenario_metrics = calculate_risk_metrics(scenario_sim)
        scenario_results(scenario_name) = scenario_metrics

    return scenario_results


stress_scenarios = {
    "Base Case": (0.0, 0.0),
    "Market Crash": (-0.20, 0.5),
    "Bear Market": (-0.10, 0.3),
    "Excessive Volatility": (0.0, 0.8),
    "Recession": (-0.15, 0.4)
}

scenario_results = scenario_stress_testing(
    annual_returns, annual_volatilities, correlation_matrix,
    portfolio_weights, initial_portfolio_value, stress_scenarios
)

scenario_df = pd.DataFrame(scenario_results).T.spherical(4)

AUSGABE:

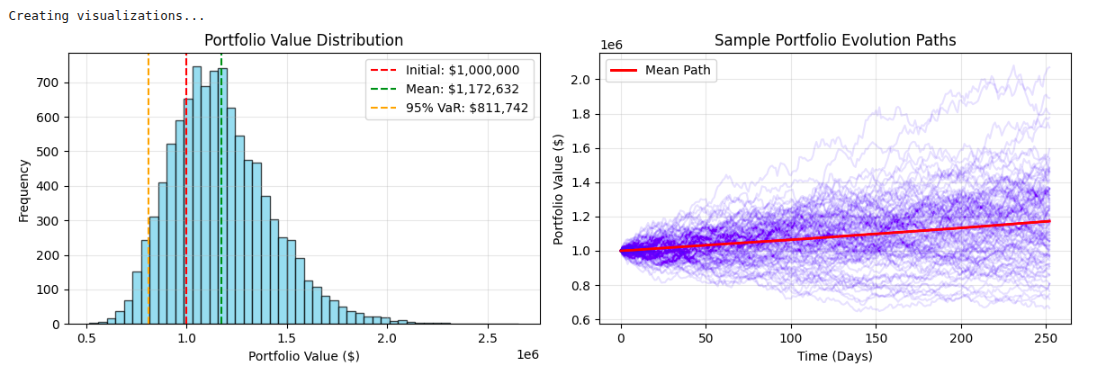
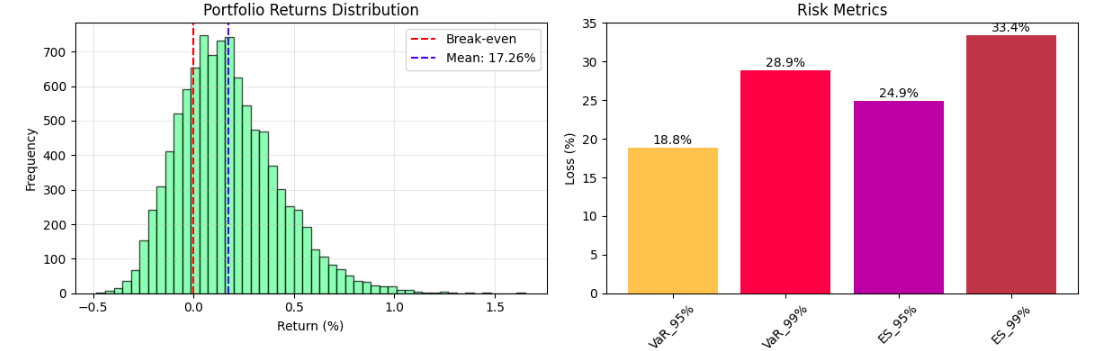
Ausgangsanalyse:

Die Simulationsausgaben vom Typ Monte Carlo bieten ein umfassendes Verständnis der Risikoanalyse durch wichtige Statistiken und Visualisierungen des potenziellen Portfoliosverhaltens in der Unsicherheit. Die VARTIC-Methoden (Worth-IT-Risiko) geben typischerweise für ein diversifiziertes Portfolio eine 5% ige Wahrscheinlichkeit an, über einen Zeithorizont von 1 Jahr mehr als 15-20% zurückzuführen zu sein. In den erwarteten Mangelkennzahlen werden die durchschnittlichen Verluste schlechter Ergebnisse angegeben. Das Histogramm der Portfoliowertverteilung ergibt den probabilistischen Ergebnisbereich und zeigt häufig ein rechtes Schiefemuster in Bezug auf das Konzentrieren des Abwärtsrisikos, während das Aufwärtspotential bleibt.

Risikobereinigte Leistungsstatistiken wie das Sharpe-Verhältnis (normalerweise im Bereich von 0,8 bis 1,5 für Portfolios mit ausgewogener Exposition) können darauf hinweisen, ob die erwartete potenzielle Rendite die Volatilitätsexposition rechtfertigt. Die Visualisierung von Simulationspfaden zeigt, dass die Marktunsicherheit im Laufe der Zeit verschärft wird, wobei individuelle Szenarien weit von der mittleren Flugbahn entfernt sind, und die Richtungsänderungen, die im Laufe der Zeit auftreten, bieten potenzielle Einblicke in die strategischen Vermögenszuweisung oder Risikomanagemententscheidungen.

Fortgeschrittene Techniken: Verbesserung von Monte -Carlo -Risikomodellen

Durch die Verwendung von Varianzreduktionstechniken können Effizienz und Genauigkeit in Monte -Carlo -Simulationen erheblich verbessert werden.

• Antithetische Variationen, Kontrollvariationen und Wichtigkeitsabtastverfahren verringern die erforderliche Anzahl von Simulationen, um das gewünschte Genauigkeitsniveau zu erreichen.
• Quasi-monte-Carlo-Methoden basieren auf Sequenzen mit niedriger Discrepanz wie „Sobol“ oder „Halton-Wiederholungen“, die häufig schneller konvergieren als Pseudo-Random-Methoden, insbesondere bei hochdimensionalen Ableitungen und Portfolio-Optimierungsproblemen.
• Copula-basierte Abhängigkeitsmodellierungsfunktionen verwenden komplexere Korrelationsstrukturen als eine einfache lineare Korrelation. „Clayton“, „Gumbel“ und „T-Copulas“ können alle Schwanzabhängigkeiten und Asymmetrien zwischen Vermögenswerten passen, um realistische Schätzungen von „Risiko“ vorzulegen.
• Sprungdiffusionsprozesse und Regime-Switching-Modelle, um plötzliche Schocks auf dem Markt zu berücksichtigen, und die Änderung der Volatilitätsregime ist etwas, das reine geometrische Brownsche Bewegung nicht modellieren kann. Die erweiterten Methoden tragen erheblich zur Verbesserung der Stresstests und zur Analyse des Schwanzrisikos bei.

Mehr lesen: Ein Leitfaden zur Monte -Carlo -Simulation

Abschluss

Die Verwendung von Python Monte -Carlo -Simulation neben Excel ist ein großer Fortschritt im quantitativen Risikomanagement. Diese hybridisierte Model verwendet effektiv die rechnerische Strenge von Python in Verbindung mit der Usability von Excel, was zu fortschrittlichen Risikomodellierungstools führt, die die Verbesserung der Benutzerfreundlichkeit zusammen mit der Funktionalität behalten. Dies bedeutet, dass Finanzfachleute fortschrittliche Szenarioanalysen, Stresstests und Portfoliooptimierung durchführen können und gleichzeitig die Vertrautheit der Excel -Plattform nutzen. Die in diesem Tutorial enthaltenen Methoden bieten ein Paradigma zum Konstruktion von unternehmensweiten Risikomanagementsystemen, bei denen sowohl die analytische Strenge als auch die Benutzerfreundlichkeit das gleiche Ziel erreichen können.

In einem sich ständig weiterentwickelnden regulatorischen und komplexen Marktumfeld wird die verbesserte Kapazität zur Anpassung und Weiterentwicklung von Risikomodellen immer relevanter. Durch die Integration von Python-Excel können wir die Flexibilität und die technischen Fähigkeiten erreichen, um diese Herausforderungen zu tragen und gleichzeitig die Transparenz und Auditabilität der Entwicklung des Risikomanagementmodells zu verbessern.

Häufig gestellte Fragen

Knowledge Science Trainee bei Analytics Vidhya
Ich arbeite derzeit als Knowledge Science Trainee bei Analytics Vidhya, wo ich mich darauf konzentriere, datengesteuerte Lösungen zu erstellen und KI/ML-Techniken anzuwenden, um reale Geschäftsprobleme zu lösen. Meine Arbeit ermöglicht es mir, erweiterte Analysen, maschinelles Lernen und KI-Anwendungen zu untersuchen, die Organisationen dazu ermöglichen, intelligentere, evidenzbasierte Entscheidungen zu treffen.
Mit einer starken Grundlage für Informatik, Softwareentwicklung und Datenanalyse bin ich leidenschaftlich, KI zu nutzen, um wirkungsvolle, skalierbare Lösungen zu schaffen, die die Lücke zwischen Technologie und Wirtschaft schließen.
📩 Sie können mich auch an mich erreichen (E -Mail geschützt)