

Bild vom Autor
Ausreißer sind abnormale Beobachtungen, die sich erheblich vom Relaxation Ihrer Daten unterscheiden. Sie können aufgrund von Experimentierfehlern, Messfehlern oder einfach aufgrund der Variabilität in den Daten selbst auftreten. Diese Ausreißer können die Leistung Ihres Modells erheblich beeinträchtigen und zu verzerrten Ergebnissen führen – ähnlich wie ein Spitzenreiter bei der relativen Benotung an Universitäten den Durchschnitt erhöhen und die Benotungskriterien beeinflussen kann. Der Umgang mit Ausreißern ist ein entscheidender Teil des Datenbereinigungsverfahrens.
In diesem Artikel erkläre ich Ihnen, wie Sie Ausreißer erkennen und auf welche Weise Sie in Ihrem Datensatz damit umgehen können.
Ausreißer erkennen
Es gibt verschiedene Methoden, um Ausreißer zu erkennen. Wenn ich sie klassifizieren müsste, sähe das Ergebnis folgendermaßen aus:
- Visualisierungsbasierte Methoden: Zeichnen Sie Streudiagramme oder Boxplots, um die Datenverteilung anzuzeigen und auf abnormale Datenpunkte zu untersuchen.
- Statistikbasierte Methoden: Diese Ansätze beinhalten Z-Scores und IQR (Interquartilsabstand), die Zuverlässigkeit bieten, aber möglicherweise weniger intuitiv sind.
Ich werde diese Methoden nicht ausführlich behandeln, um beim Thema zu bleiben. Ich werde jedoch am Ende einige Referenzen zur Erläuterung angeben. In unserem Beispiel verwenden wir die IQR-Methode. So funktioniert diese Methode:
IQR (Interquartilsabstand) = Q3 (75. Perzentil) – Q1 (25. Perzentil)
Die IQR-Methode besagt, dass alle Datenpunkte unter Q1 – 1,5 * IQR oder höher Q3 + 1,5 * IQR werden als Ausreißer markiert. Lassen Sie uns einige zufällige Datenpunkte generieren und die Ausreißer mit dieser Methode erkennen.
Führen Sie die erforderlichen Importe durch und generieren Sie die Zufallsdaten mit np.random:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Generate random knowledge
np.random.seed(42)
knowledge = pd.DataFrame({
'worth': np.random.regular(0, 1, 1000)
})Ermitteln Sie die Ausreißer im Datensatz mit der IQR-Methode:
# Perform to detect outliers utilizing IQR
def detect_outliers_iqr(knowledge):
Q1 = knowledge.quantile(0.25)
Q3 = knowledge.quantile(0.75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
return (knowledge < lower_bound) | (knowledge > upper_bound)
# Detect outliers
outliers = detect_outliers_iqr(knowledge('worth'))
print(f"Variety of outliers detected: {sum(outliers)}")Ausgabe ⇒ Anzahl der erkannten Ausreißer: 8
Visualisieren Sie den Datensatz mithilfe von Streu- und Boxplots, um zu sehen, wie er aussieht
# Visualize the info with outliers utilizing scatter plot and field plot
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Scatter plot
ax1.scatter(vary(len(knowledge)), knowledge('worth'), c=('blue' if not x else 'pink' for x in outliers))
ax1.set_title('Dataset with Outliers Highlighted (Scatter Plot)')
ax1.set_xlabel('Index')
ax1.set_ylabel('Worth')
# Field plot
sns.boxplot(x=knowledge('worth'), ax=ax2)
ax2.set_title('Dataset with Outliers (Field Plot)')
ax2.set_xlabel('Worth')
plt.tight_layout()
plt.present()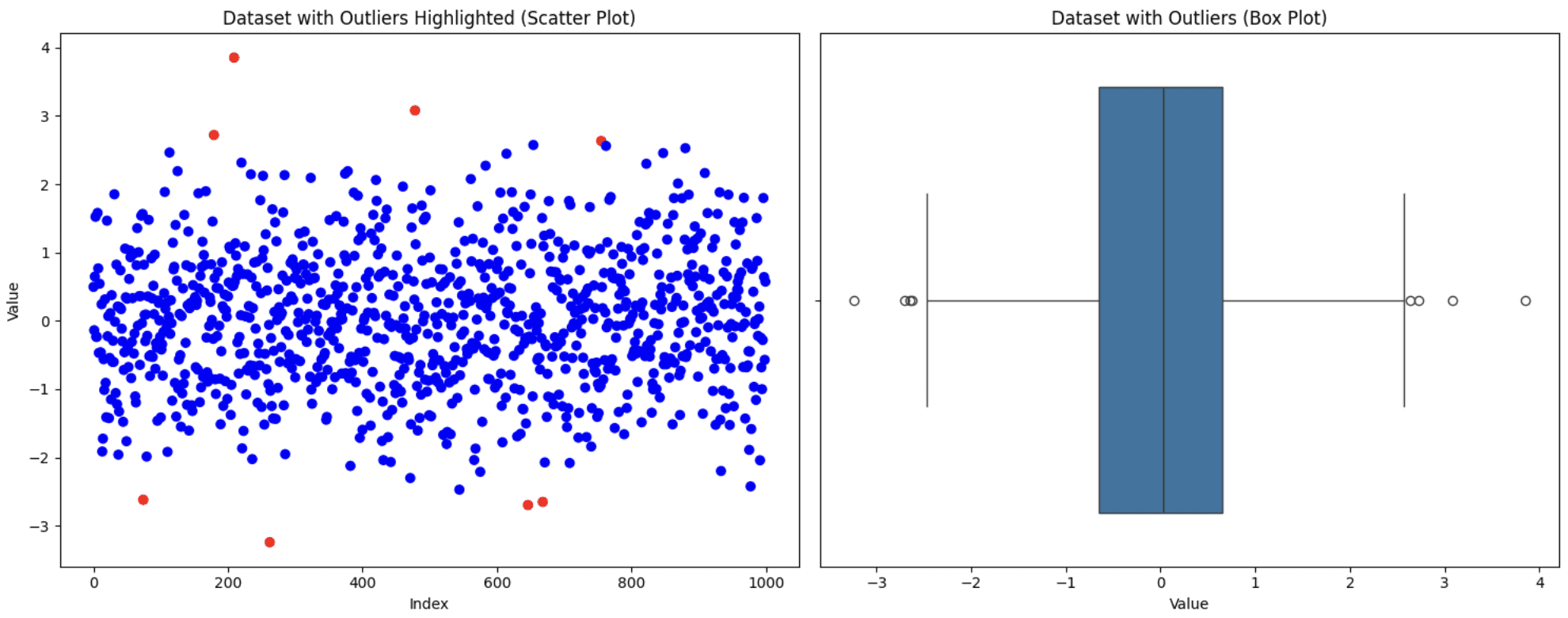

Ursprünglicher Datensatz
Nachdem wir nun die Ausreißer erkannt haben, besprechen wir einige der verschiedenen Möglichkeiten zum Umgang mit den Ausreißern.
Umgang mit Ausreißern
1. Ausreißer entfernen
Dies ist einer der einfachsten Ansätze, aber nicht immer der richtige. Sie müssen bestimmte Faktoren berücksichtigen. Wenn das Entfernen dieser Ausreißer die Größe Ihres Datensatzes erheblich reduziert oder wenn sie wertvolle Erkenntnisse enthalten, ist es nicht die beste Entscheidung, sie aus Ihrer Analyse auszuschließen. Wenn sie jedoch auf Messfehler zurückzuführen sind und nur wenige vorhanden sind, ist dieser Ansatz geeignet. Wenden wir diese Technik auf den oben generierten Datensatz an:
# Take away outliers
data_cleaned = knowledge(~outliers)
print(f"Unique dataset measurement: {len(knowledge)}")
print(f"Cleaned dataset measurement: {len(data_cleaned)}")
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Scatter plot
ax1.scatter(vary(len(data_cleaned)), data_cleaned('worth'))
ax1.set_title('Dataset After Eradicating Outliers (Scatter Plot)')
ax1.set_xlabel('Index')
ax1.set_ylabel('Worth')
# Field plot
sns.boxplot(x=data_cleaned('worth'), ax=ax2)
ax2.set_title('Dataset After Eradicating Outliers (Field Plot)')
ax2.set_xlabel('Worth')
plt.tight_layout()
plt.present()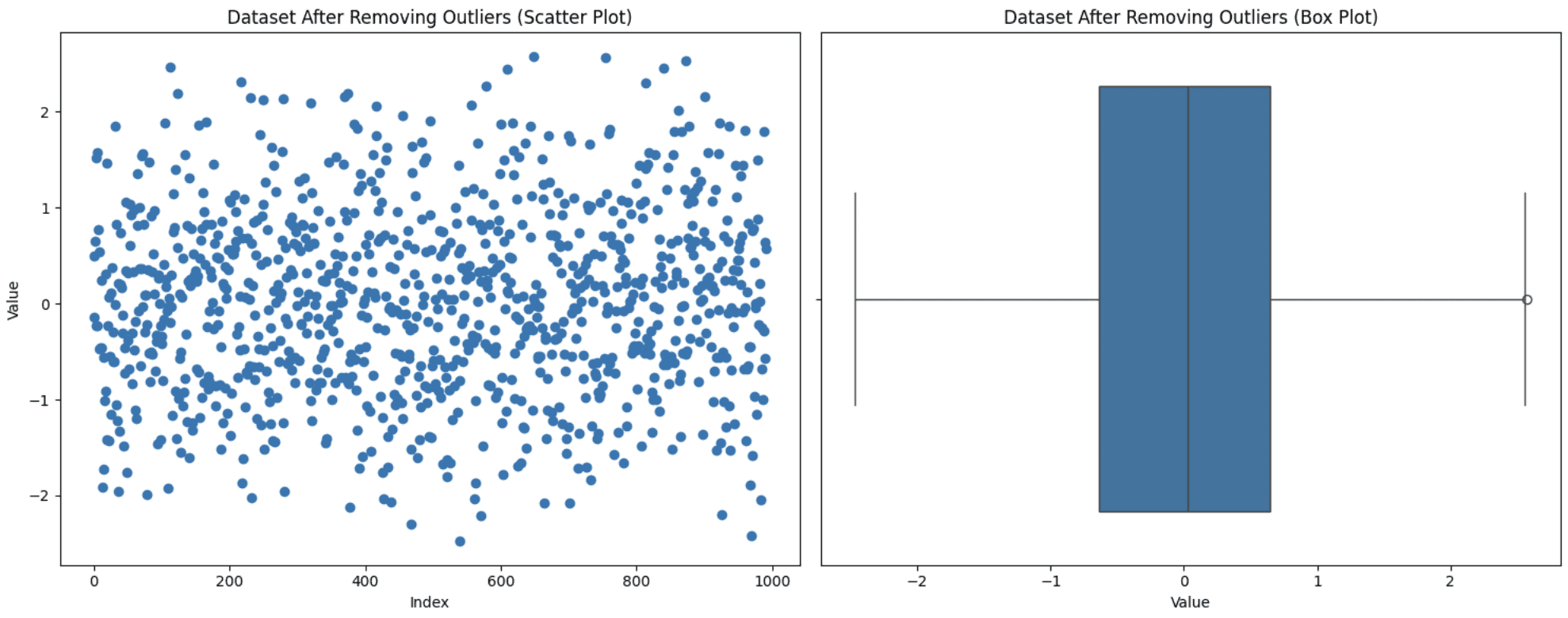

Ausreißer entfernen
Beachten Sie, dass die Verteilung der Daten durch das Entfernen von Ausreißern tatsächlich geändert werden kann. Wenn Sie einige anfängliche Ausreißer entfernen, kann sich die Definition eines Ausreißers durchaus ändern. Daher können Daten, die zuvor im normalen Bereich gelegen hätten, unter einer neuen Verteilung als Ausreißer betrachtet werden. Sie können einen neuen Ausreißer mit dem neuen Boxplot sehen.
2. Begrenzung von Ausreißern
Diese Technik wird verwendet, wenn Sie Ihre Datenpunkte nicht verwerfen möchten, aber das Beibehalten dieser Extremwerte Ihre Analyse beeinträchtigen kann. Sie legen additionally einen Schwellenwert für die Maximal- und Minimalwerte fest und bringen dann die Ausreißer in diesen Bereich. Sie können diese Begrenzung auch auf Ausreißer oder auf Ihren gesamten Datensatz anwenden. Wenden wir die Begrenzungsstrategie auf unseren gesamten Datensatz an, um ihn in den Bereich des 5. bis 95. Perzentils zu bringen. So können Sie dies ausführen:
def cap_outliers(knowledge, lower_percentile=5, upper_percentile=95):
lower_limit = np.percentile(knowledge, lower_percentile)
upper_limit = np.percentile(knowledge, upper_percentile)
return np.clip(knowledge, lower_limit, upper_limit)
knowledge('value_capped') = cap_outliers(knowledge('worth'))
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Scatter plot
ax1.scatter(vary(len(knowledge)), knowledge('value_capped'))
ax1.set_title('Dataset After Capping Outliers (Scatter Plot)')
ax1.set_xlabel('Index')
ax1.set_ylabel('Worth')
# Field plot
sns.boxplot(x=knowledge('value_capped'), ax=ax2)
ax2.set_title('Dataset After Capping Outliers (Field Plot)')
ax2.set_xlabel('Worth')
plt.tight_layout()
plt.present()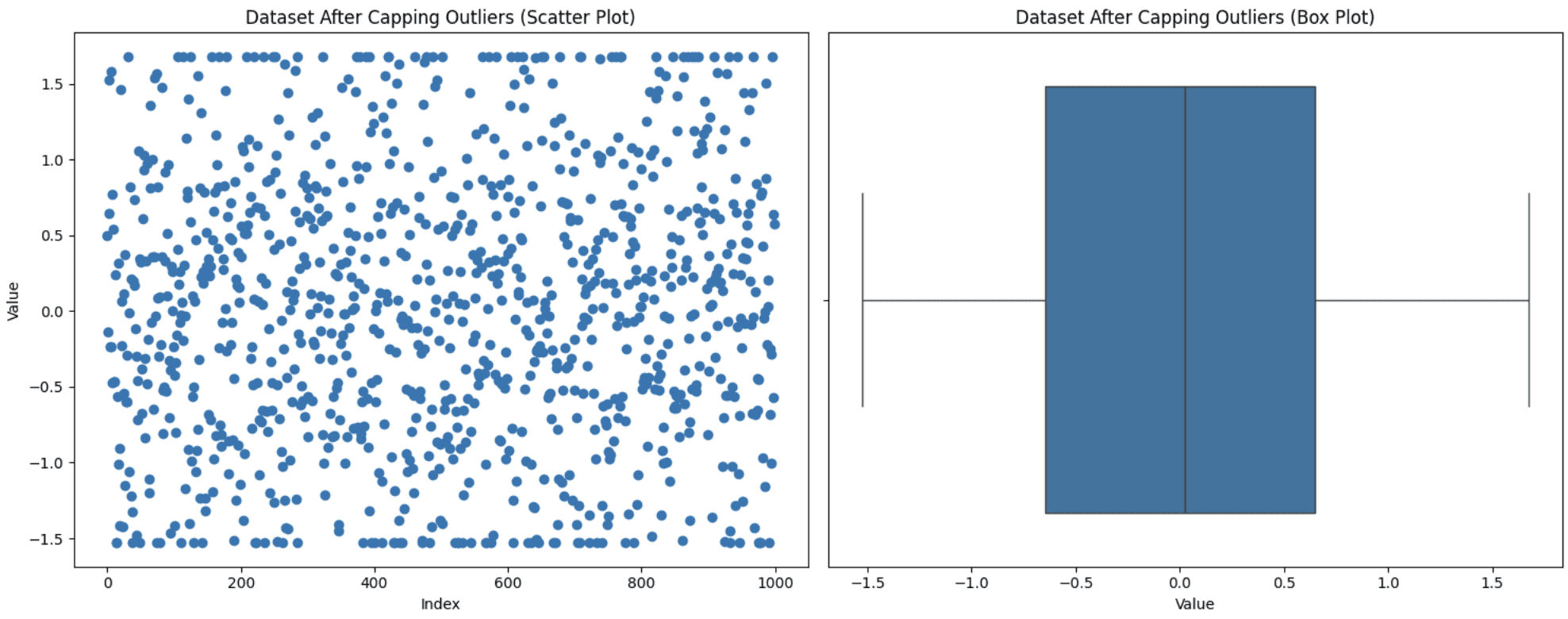

Begrenzung von Ausreißern
Sie können der Grafik entnehmen, dass die oberen und unteren Punkte im Streudiagramm aufgrund der Kappung auf einer Linie zu liegen scheinen.
3. Imputation von Ausreißern
Manchmal ist das Entfernen von Werten aus der Analyse keine Choice, da dies zu Informationsverlust führen kann und Sie diese Werte auch nicht wie beim Capping auf Most oder Minimal setzen möchten. In dieser Scenario besteht ein anderer Ansatz darin, diese Werte durch aussagekräftigere Optionen wie Mittelwert, Median oder Modus zu ersetzen. Die Auswahl variiert je nach beobachtetem Datenbereich, achten Sie jedoch darauf, bei der Verwendung dieser Technik keine Verzerrungen einzuführen. Ersetzen wir unsere Ausreißer durch den Moduswert (den am häufigsten vorkommenden Wert) und sehen wir uns an, wie das Diagramm aussieht:
knowledge('value_imputed') = knowledge('worth').copy()
median_value = knowledge('worth').median()
knowledge.loc(outliers, 'value_imputed') = median_value
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Scatter plot
ax1.scatter(vary(len(knowledge)), knowledge('value_imputed'))
ax1.set_title('Dataset After Imputing Outliers (Scatter Plot)')
ax1.set_xlabel('Index')
ax1.set_ylabel('Worth')
# Field plot
sns.boxplot(x=knowledge('value_imputed'), ax=ax2)
ax2.set_title('Dataset After Imputing Outliers (Field Plot)')
ax2.set_xlabel('Worth')
plt.tight_layout()
plt.present()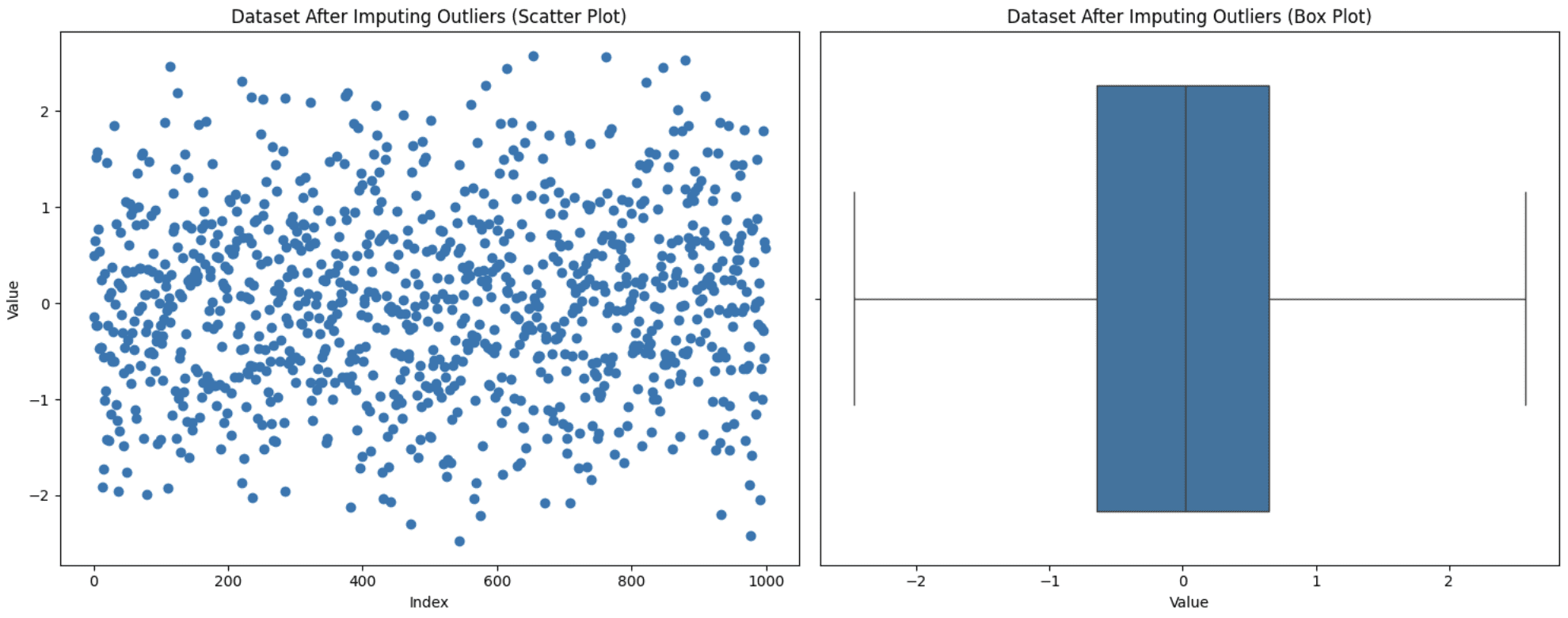

Imputation von Ausreißern
Beachten Sie, dass wir jetzt keine Ausreißer haben. Dies garantiert jedoch nicht, dass Ausreißer entfernt werden, da sich nach der Imputation auch der IQR ändert. Sie müssen experimentieren, um herauszufinden, was in Ihrem Fall am besten passt.
4. Anwenden einer Transformation
Die Transformation wird auf Ihren gesamten Datensatz angewendet, nicht auf bestimmte Ausreißer. Sie ändern im Grunde die Darstellung Ihrer Daten, um die Auswirkungen der Ausreißer zu reduzieren. Es gibt verschiedene Transformationstechniken wie Log-Transformation, Quadratwurzeltransformation, Field-Cox-Transformation, Z-Skalierung, Yeo-Johnson-Transformation, Min-Max-Skalierung usw. Die Wahl der richtigen Transformation für Ihren Fall hängt von der Artwork der Daten und Ihrem Endziel der Analyse ab. Hier sind einige Tipps, die Ihnen bei der Auswahl der richtigen Transformationstechnik helfen:
- Für rechtsschiefe Daten: Verwenden Sie die Log-, Quadratwurzel- oder Field-Cox-Transformation. Log ist sogar noch besser, wenn Sie kleine Zahlenwerte komprimieren möchten, die über einen großen Maßstab verteilt sind. Quadratwurzel ist besser, wenn Sie neben der Rechtsschiefe eine weniger excessive Transformation wünschen und auch Nullwerte verarbeiten möchten, während Field-Cox Ihre Daten auch normalisiert, was bei den anderen beiden nicht der Fall ist.
- Für linksschiefe Daten: Reflektieren Sie zuerst die Daten und wenden Sie dann die genannten Techniken für rechtsschiefe Daten an.
- So stabilisieren Sie die Varianz: Verwenden Sie Field-Cox oder Yeo-Johnson (ähnlich wie Field-Cox, verarbeitet jedoch auch Null- und destructive Werte).
- Zur Mittelwertzentrierung und Skalierung: Verwenden Sie die Z-Rating-Standardisierung (Standardabweichung = 1).
- Für bereichsgebundene Skalierung (fester Bereich, d. h. (2,5)): Verwenden Sie die Min-Max-Skalierung.
Lassen Sie uns einen rechtsschiefen Datensatz generieren und die Log-Transformation auf die gesamten Daten anwenden, um zu sehen, wie das funktioniert:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Generate right-skewed knowledge
np.random.seed(42)
knowledge = np.random.exponential(scale=2, measurement=1000)
df = pd.DataFrame(knowledge, columns=('worth'))
# Apply Log Transformation (shifted to keep away from log(0))
df('log_value') = np.log1p(df('worth'))
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# Unique Information - Scatter Plot
axes(0, 0).scatter(vary(len(df)), df('worth'), alpha=0.5)
axes(0, 0).set_title('Unique Information (Scatter Plot)')
axes(0, 0).set_xlabel('Index')
axes(0, 0).set_ylabel('Worth')
# Unique Information - Field Plot
sns.boxplot(x=df('worth'), ax=axes(0, 1))
axes(0, 1).set_title('Unique Information (Field Plot)')
axes(0, 1).set_xlabel('Worth')
# Log Remodeled Information - Scatter Plot
axes(1, 0).scatter(vary(len(df)), df('log_value'), alpha=0.5)
axes(1, 0).set_title('Log Remodeled Information (Scatter Plot)')
axes(1, 0).set_xlabel('Index')
axes(1, 0).set_ylabel('Log(Worth)')
# Log Remodeled Information - Field Plot
sns.boxplot(x=df('log_value'), ax=axes(1, 1))
axes(1, 1).set_title('Log Remodeled Information (Field Plot)')
axes(1, 1).set_xlabel('Log(Worth)')
plt.tight_layout()
plt.present()


Anwenden der Protokolltransformation
Sie können sehen, dass eine einfache Transformation die meisten Ausreißer selbst behandelt und auf nur einen reduziert hat. Dies zeigt die Leistungsfähigkeit der Transformation beim Umgang mit Ausreißern. In diesem Fall ist es notwendig, vorsichtig zu sein und Ihre Daten intestine genug zu kennen, um die geeignete Transformation auszuwählen, da andernfalls Probleme auftreten können.
Einpacken
Damit sind wir am Ende unserer Diskussion über Ausreißer, verschiedene Möglichkeiten, sie zu erkennen und wie man mit ihnen umgeht. Dieser Artikel ist Teil der Pandas-Reihe, und Sie können weitere Artikel auf meiner Autorenseite nachlesen. Wie oben erwähnt, finden Sie hier einige zusätzliche Ressourcen, mit denen Sie mehr über Ausreißer erfahren können:
- Methoden zur Ausreißererkennung im maschinellen Lernen
- Verschiedene Transformationen im maschinellen Lernen
- Arten von Transformationen für eine bessere Normalverteilung
Kanwal Mehreen Kanwal ist Ingenieurin für maschinelles Lernen und technische Autorin mit einer tiefen Leidenschaft für Datenwissenschaft und die Schnittstelle zwischen KI und Medizin. Sie ist Mitautorin des E-Books „Maximizing Productiveness with ChatGPT“. Als Google Technology Scholar 2022 für APAC setzt sie sich für Vielfalt und akademische Exzellenz ein. Sie ist außerdem als Teradata Variety in Tech Scholar, Mitacs Globalink Analysis Scholar und Harvard WeCode Scholar anerkannt. Kanwal ist eine leidenschaftliche Verfechterin des Wandels und hat FEMCodes gegründet, um Frauen in MINT-Fächern zu stärken.
