Einführung
Stellen Sie sich vor, Sie führen eine Studie durch, um festzustellen, ob ein neues Medikament den Blutdruck wirksam senkt. Sie verabreichen das Medikament einer Gruppe von Patienten und vergleichen deren Ergebnisse mit denen einer Kontrollgruppe, die ein Placebo erhält. Sie analysieren die Daten und kommen zu dem Schluss, dass das neue Medikament den Blutdruck deutlich senkt, obwohl dies in Wirklichkeit nicht der Fall ist. Diese irrtümliche Ablehnung der Nullhypothese (dass das Medikament keine Wirkung hat) ist ein Fehler 1. Artwork. Nehmen wir andererseits an, das Medikament senkt den Blutdruck tatsächlich, aber Ihre Studie kann diesen Effekt aufgrund unzureichender Stichprobengröße oder Variabilität der Daten nicht feststellen. Sie kommen daher zu dem Schluss, dass das Medikament unwirksam ist, was ein Versäumnis ist, eine falsche Nullhypothese abzulehnen – ein Fehler 2. Artwork.
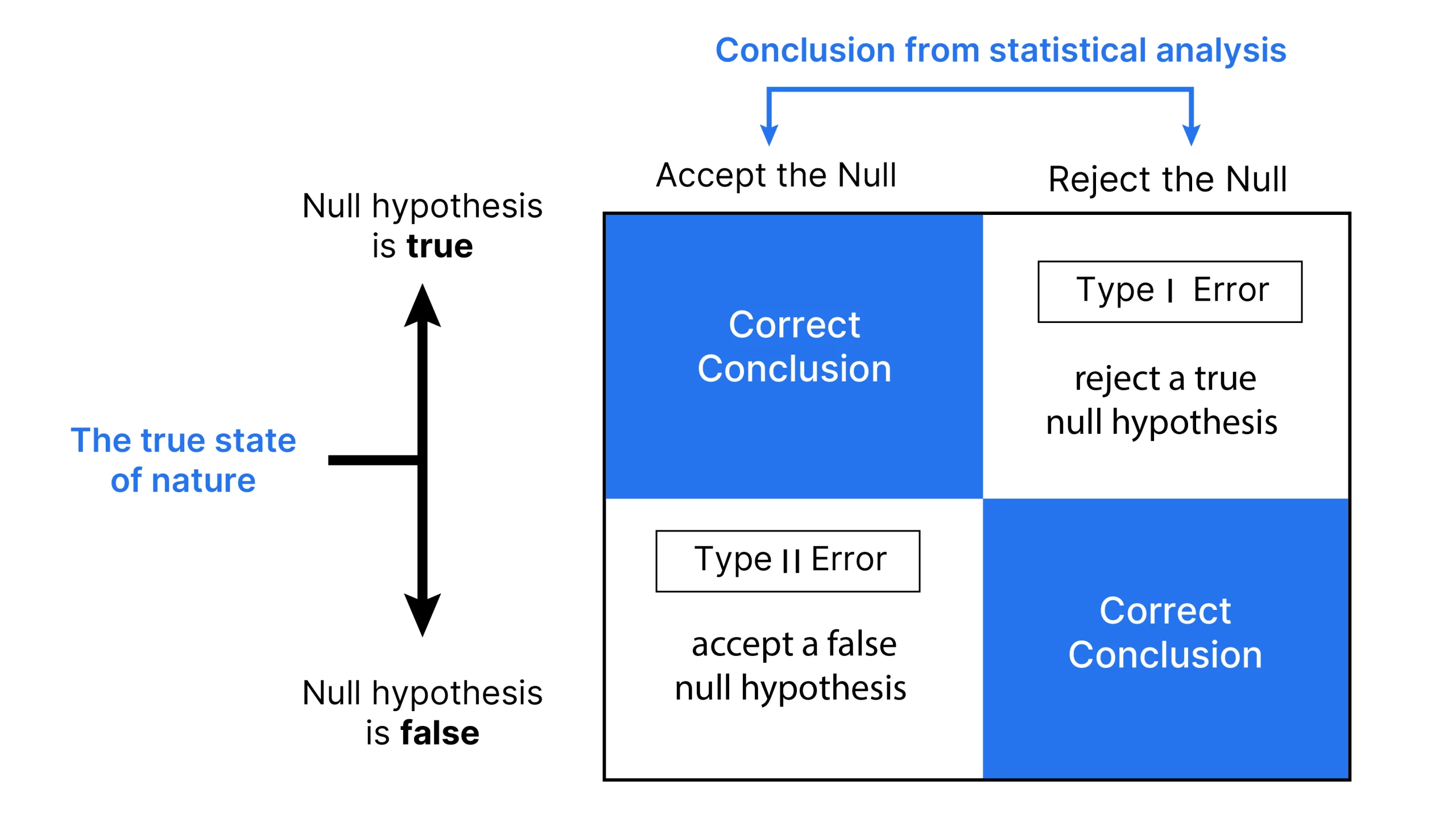
Diese Szenarien unterstreichen, wie wichtig es ist, Fehler vom Typ I und Typ II bei statistischen Exams zu verstehen. Fehler vom Typ I, auch als falsch-positive Ergebnisse bekannt, treten auf, wenn wir irrtümlicherweise eine wahre Nullhypothese ablehnen. Fehler vom Typ II oder falsch-negative Ergebnisse treten auf, wenn wir eine falsche Nullhypothese nicht ablehnen. Ein Großteil der statistischen Theorie dreht sich um die Minimierung dieser Fehler, obwohl es statistisch unmöglich ist, beide Fehler vollständig zu eliminieren. Wenn wir diese Konzepte verstehen, können wir in verschiedenen Bereichen, von medizinischen Exams bis hin zur Qualitätskontrolle in der Fertigung, fundiertere Entscheidungen treffen.
Überblick
- Fehler vom Typ I und Typ II stellen falsch-positive und falsch-negative Ergebnisse bei Hypothesentests dar.
- Beim Hypothesentesten geht es darum, Null- und Alternativhypothesen zu formulieren, ein Signifikanzniveau auszuwählen, Teststatistiken zu berechnen und Entscheidungen auf der Grundlage kritischer Werte zu treffen.
- Fehler vom Typ I treten auf, wenn eine echte Nullhypothese fälschlicherweise abgelehnt wird, was zu unnötigen Eingriffen führt.
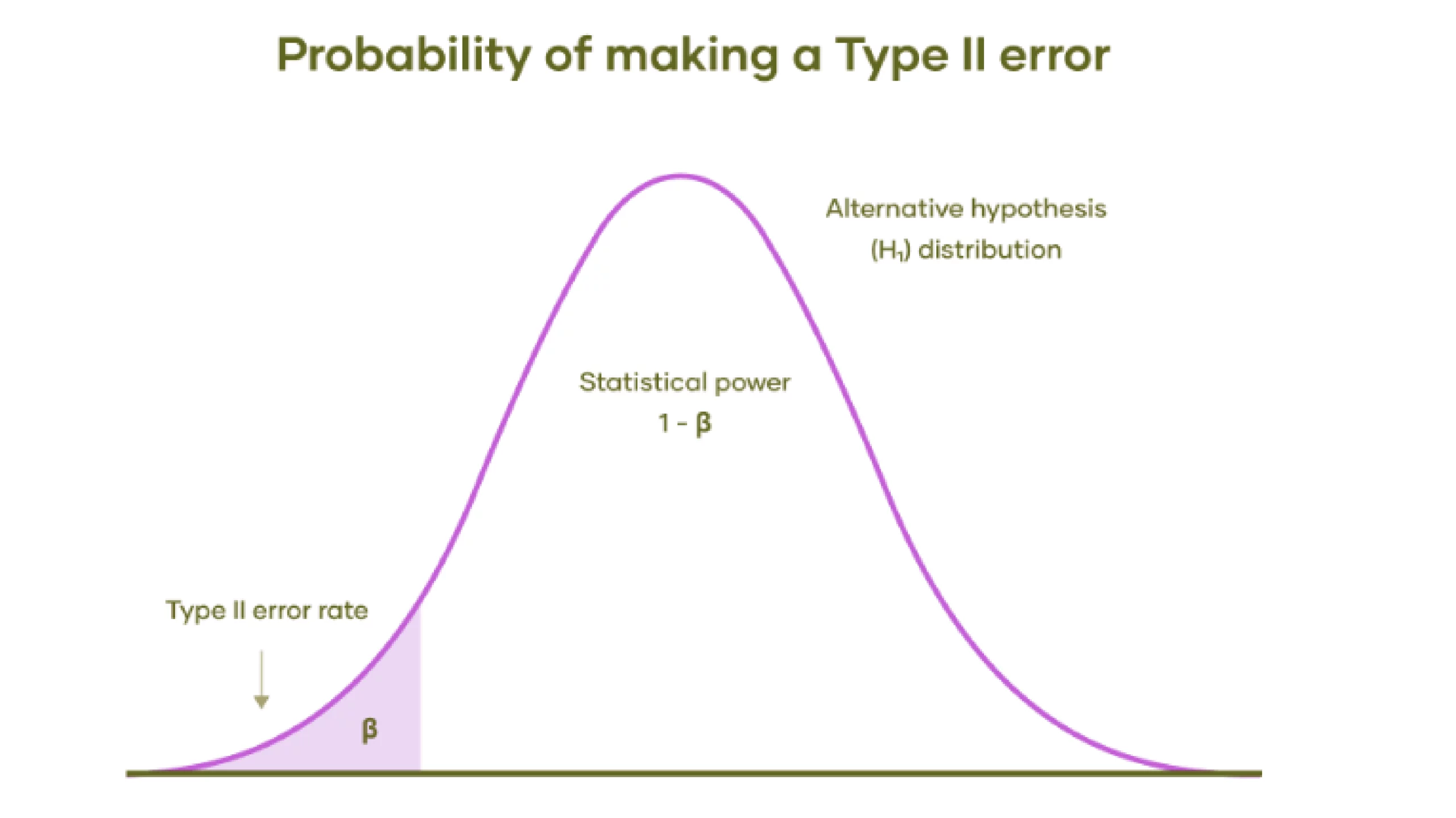
- Fehler vom Typ II treten auf, wenn eine falsche Nullhypothese nicht zurückgewiesen wird und dies zu Fehldiagnosen oder übersehenen Effekten führt.
- Der Ausgleich von Fehlern des Typs I und Typs II erfordert Kompromisse bei Signifikanzniveaus, Stichprobengrößen und Teststärke, um beide Fehler wirksam zu minimieren.
Die Grundlagen des Hypothesentests
Hypothesentest ist eine Methode, mit der entschieden wird, ob genügend Beweise vorliegen, um eine Nullhypothese (H₀) zugunsten einer Alternativhypothese (H₁) abzulehnen. Der Prozess umfasst:
- Hypothesen formulieren
- Keine Wirkung oder kein Unterschied: Keine Wirkung oder kein Unterschied.
- Alternativhypothese (H₁): Es liegt eine Auswirkung bzw. ein Unterschied vor.
- Wahl eines Signifikanzniveaus (α): Der Wahrscheinlichkeitsschwellenwert für die Ablehnung von H₀ wird normalerweise auf 0,05, 0,01 oder 0,10 festgelegt.
- Berechnung der Teststatistik: Ein aus Beispieldaten abgeleiteter Wert, der zum Vergleich mit einem kritischen Wert verwendet wird.
- Eine Entscheidung treffen: Wenn die Teststatistik den entscheidenden Wert überschreitet, lehnen Sie H₀ ab, andernfalls lehnen Sie H₀ nicht ab.
Lesen Sie auch: Finish-to-Finish-Statistiken für Information Science
Fehler 1. Artwork (Falsch-Positiv)
Ein Fehler Typ I tritt auf, wenn die Nullhypothese (H0) eines Experiments zwar zutrifft, aber fälschlicherweise abgelehnt wird (die Grafik wird unten erwähnt).
Dieser Fehler stellt die Identifizierung von etwas dar, das tatsächlich nicht vorhanden ist, ähnlich einem falsch positiven Ergebnis. Dies kann anhand eines einfachen Beispiels erklärt werden: Bei einem medizinischen Check auf eine Krankheit würde ein Fehler Typ I bedeuten, dass der Check anzeigt, dass ein Affected person die Krankheit hat, obwohl dies nicht der Fall ist, was im Wesentlichen einen falschen Alarm auslöst. In diesem Fall würde die Nullhypothese (H0) lauten: Der Affected person hat keine Krankheit.
Die Wahrscheinlichkeit, einen Fehler erster Artwork zu begehen, wird als Signifikanzniveau oder Rateniveau bezeichnet. Es wird durch den griechischen Buchstaben α (Alpha) gekennzeichnet und ist als Alpha-Niveau bekannt. Normalerweise wird diese Likelihood oder Wahrscheinlichkeit auf 0,05 oder 5 % festgelegt. Auf diese Weise sind Forscher normalerweise geneigt, eine 5-prozentige Likelihood zu akzeptieren, die Nullhypothese fälschlicherweise abzulehnen, wenn sie tatsächlich zutreffend ist.
Fehler des Typs I können zu unnötigen Behandlungen oder Eingriffen führen und so Stress und potenzielle Schäden für den Einzelnen verursachen.
Lassen Sie uns dies anhand eines Diagramms verstehen:
- Nullhypothesenverteilung: Die Glockenkurve zeigt die Bandbreite möglicher Ergebnisse, wenn die Nullhypothese zutrifft. Das bedeutet, dass die Ergebnisse auf Zufall beruhen, ohne dass es tatsächliche Auswirkungen oder Unterschiede gibt.
- Fehlerrate Typ I: Der schattierte Bereich unter dem Kurvenende stellt das Signifikanzniveau α dar. Es ist die Wahrscheinlichkeit, die Nullhypothese abzulehnen, obwohl sie tatsächlich wahr ist. Dies führt zu einem Fehler 1. Artwork (falsch positiv).
Fehler 2. Artwork (Falsch-Negativ)
Ein Fehler vom Typ II tritt auf, wenn eine gültige Different Hypothese wird nicht erkannt. Einfacher ausgedrückt ist es so, als würde man einen Bären nicht entdecken, der tatsächlich da ist, und deshalb keinen Alarm auslösen, wenn es nötig wäre. In diesem Szenario lautet die Nullhypothese (H0) immer noch: „Es gibt keinen Bären.“ Der Ermittler begeht einen Fehler zweiter Artwork, wenn ein Bär anwesend, aber unentdeckt ist.
Die Hauptschwierigkeit besteht nicht immer darin, ob die Krankheit tatsächlich existiert, sondern ob sie richtig diagnostiziert wird. Der Fehler kann auf zwei Arten entstehen: entweder dadurch, dass die Krankheit nicht entdeckt wird, obwohl sie vorhanden ist, oder dadurch, dass behauptet wird, die Krankheit entdeckt zu haben, obwohl sie nicht vorhanden ist.
Die Wahrscheinlichkeit eines Fehlers zweiter Artwork wird mit dem griechischen Buchstaben β (Beta) bezeichnet. Dieser Wert bezieht sich auf die statistische Aussagekraft eines Exams, die als 1 minus β (1−β) berechnet wird.
Fehler vom Typ II können zu Fehldiagnosen oder übersehenen Auswirkungen führen und so eine unzureichende Behandlung oder Intervention zur Folge haben.
Lassen Sie uns dies anhand eines Diagramms verstehen:
- Different Hypothesenverteilung: Die Glockenkurve stellt den Bereich möglicher Ergebnisse dar, wenn die Alternativhypothese zutrifft. Dies bedeutet, dass im Gegensatz zur Nullhypothese tatsächlich ein Effekt oder Unterschied vorliegt.
- Fehlerrate 2. Artwork (β): Der schattierte Bereich unter dem linken Ende der Verteilung stellt die Wahrscheinlichkeit eines Fehlers zweiter Artwork dar.
- Statistische Energy (1 – β): Der nicht schattierte Bereich unter der Kurve rechts neben dem schattierten Bereich stellt die statistische Aussagekraft des Exams dar. Die statistische Aussagekraft ist die Wahrscheinlichkeit, die Nullhypothese korrekt abzulehnen, wenn die Alternativhypothese wahr ist. Eine höhere Aussagekraft bedeutet eine geringere Wahrscheinlichkeit, einen Fehler 2. Artwork zu machen.
Lesen Sie auch: Erfahren Sie alles über Hypothesentests!
Vergleich von Typ I- und Typ II-Fehlern
Hier ist der detaillierte Vergleich:
| Aspekt | Fehler 1. Artwork | Fehler 2. Artwork |
|---|---|---|
| Definition und Terminologie | Ablehnung einer wahren Nullhypothese (falsch-positiv) | Akzeptieren einer falschen Nullhypothese (falsch-negativ) |
| Symbolische Darstellung | α (Alpha) | β (Beta) |
| Wahrscheinlichkeit und Bedeutung | Entspricht dem für den Check festgelegten Signifikanzniveau | Berechnet als 1 minus der Teststärke (1 – Stärke) |
| Strategien zur Fehlerreduzierung | Senkung des Signifikanzniveaus (erhöht Typ-II-Fehler) | Erhöhen Sie das Signifikanzniveau (erhöht Typ-I-Fehler) |
| Kausale Faktoren | Zufall oder Glück | Kleinere Stichprobengrößen oder weniger aussagekräftige statistische Exams |
| Analogien | „Fehltreffer“ in einem Detektionssystem | „Miss“ in einem Erkennungssystem |
| Hypothesenassoziation | Falsche Ablehnung der Nullhypothese | Eine falsche Nullhypothese nicht ablehnen |
| Auftretensbedingungen | Tritt auf, wenn die Akzeptanzniveaus zu großzügig sind | Tritt auf, wenn die Annahmekriterien zu streng sind |
| Auswirkungen | Vorrangig in Bereichen, in denen die Vermeidung falscher Positivergebnisse von entscheidender Bedeutung ist (z. B. klinische Exams) | Vorrangig in Bereichen, in denen die Vermeidung falsch-negativer Ergebnisse von entscheidender Bedeutung ist (z. B. Screening auf schwere Krankheiten) |
Lesen Sie auch: Hypothesentests leicht gemacht für Information Science-Anfänger
Kompromiss zwischen Typ I- und Typ II-Fehlern
Meistens besteht ein Kompromiss zwischen Fehlern des Typs I und Typ II. Die Verringerung der Wahrscheinlichkeit eines Fehlertyps erhöht im Allgemeinen die Möglichkeit des entgegengesetzten.
- Signifikanzniveau (α): Eine Verringerung von α verringert die Wahrscheinlichkeit eines Fehlers erster Artwork, erhöht jedoch das Risiko eines Fehlers zweiter Artwork. Eine Erhöhung von α hat den gegenteiligen Effekt.
- Probengröße: Durch eine Erhöhung der Stichprobengröße können sowohl Fehler vom Typ I als auch vom Typ II reduziert werden, da größere Stichproben genauere Schätzungen liefern.
- Testleistung: Die Wahrscheinlichkeit von Fehlern des Typs II kann verringert werden, indem man die Testaussagekraft durch eine Vergrößerung der Stichprobengröße oder die Verwendung sensitiverer Exams erhöht.
Abschluss
Fehler vom Typ I und Typ II sind grundlegende Konzepte in Statistik und Forschungstechniken. Wenn wir den Unterschied zwischen diesen Fehlern und ihren Auswirkungen kennen, können wir Forschungsergebnisse besser interpretieren, leistungsfähigere Forschung betreiben und fundiertere Entscheidungen in verschiedenen Bereichen treffen. Denken Sie daran, dass das Ziel nicht darin besteht, Fehler zu eliminieren (was unmöglich ist), sondern sie basierend auf dem jeweiligen Kontext und den möglichen Ergebnissen erfolgreich zu bewältigen.
Häufig gestellte Fragen
Antwort: Es ist eine Herausforderung, beide Fehlerarten zu eliminieren, da die Reduzierung der einen Fehlerart oft die andere vergrößert. Durch eine Vergrößerung der Stichprobengröße und eine sorgfältige Studiengestaltung können Forscher jedoch beide Fehlerarten auf ein anwendbares Maß reduzieren.
Antwort: Hier sind die häufigsten Missverständnisse über Fehler vom Typ I und Typ II:
Missverständnis: Ein niedrigeres α bedeutet immer einen besseren Check.
Wirklichkeit: Ein niedrigeres α verringert zwar die Fehler des Typs I, kann jedoch zu einer Erhöhung der Fehler des Typs II führen, was dazu führt, dass wahre Effekte nicht erkannt werden.
Missverständnis: Bei großen Stichprobengrößen besteht kein Grund zur Sorge über diese Fehler.
Realität: Große Stichproben reduzieren Fehler, können sie aber nicht ausschließen. Ein gutes Studiendesign ist nach wie vor unerlässlich.
Missverständnis: Ein signifikantes Ergebnis (p-Wert < α) bedeutet, dass die Nullhypothese falsch ist.
Wirklichkeit: Ein signifikantes Ergebnis deutet auf Beweise gegen H₀ hin, beweist aber nicht, dass H₀ falsch ist. Andere Faktoren wie Studiendesign und Kontext müssen berücksichtigt werden.
Antwort: Wenn Sie die Aussagekraft Ihres Exams erhöhen, ist es wahrscheinlicher, dass ein echter Effekt erkannt wird. Sie können dies folgendermaßen erreichen:
A. Erhöhen Sie Ihre Stichprobengröße.
B. Verwendung präziserer Messungen.
C. Reduzieren Sie die Variabilität Ihrer Daten.
D. Erhöhen Sie die Effektgröße, wenn möglich.
Antwort: Pilotstudien helfen Ihnen, die Parameter abzuschätzen, die für die Gestaltung einer größeren, aussagekräftigeren Studie erforderlich sind. Sie liefern erste Daten zu Effektgrößen und Variabilität, die Ihre Stichprobengrößenberechnungen unterstützen und dabei helfen, Fehler vom Typ I und Typ II in der Hauptstudie auszugleichen.
