Was ist ein Eigenvektor und ein Eigenwert?

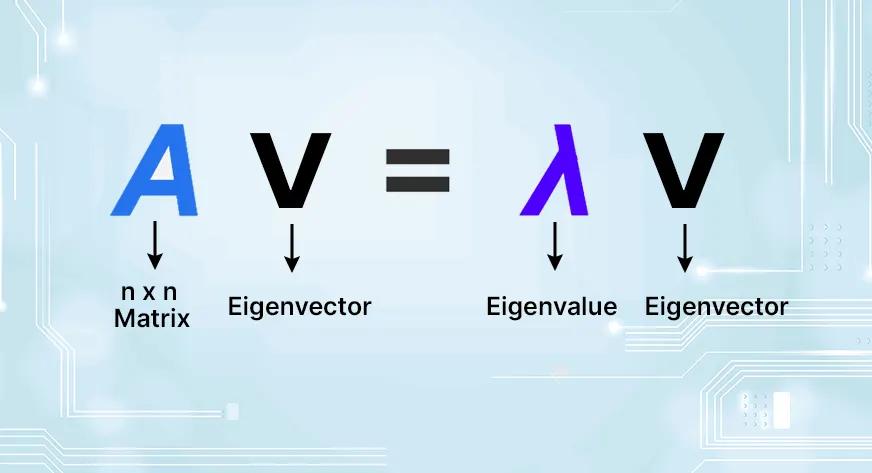
Die lineare Algebra ist ein Eckpfeiler vieler fortgeschrittener mathematischer Konzepte und wird häufig in den Bereichen Datenwissenschaft, maschinelles Lernen, Laptop Imaginative and prescient und Ingenieurwesen eingesetzt. Eines der Grundkonzepte der linearen Algebra sind Eigenvektoren, oft gepaart mit Eigenwerten. Aber was genau ist ein Eigenvektor und warum ist er so wichtig?

In diesem Artikel wird das Konzept der Eigenvektoren auf einfache und intuitive Weise aufgeschlüsselt, sodass es für jedermann leicht verständlich ist.

Was ist ein Eigenvektor?

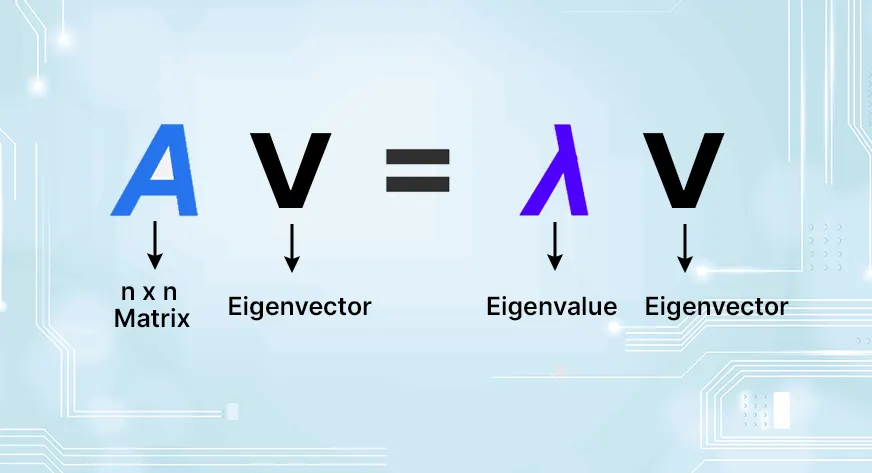
Einer quadratischen Matrix ist ein spezieller Vektortyp zugeordnet, der Eigenvektor genannt wird. Wenn die Matrix auf den Eigenvektor einwirkt, behält sie die Richtung des Eigenvektors unverändert bei und skaliert ihn nur um einen Skalarwert, den sogenannten Eigenwert.

Mathematisch gesehen ist für eine quadratische Matrix A ein Vektor v ungleich Null ein Eigenvektor, wenn:

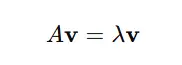
Hier:

• A ist die Matrix.
• v ist der Eigenvektor.
• λ ist der Eigenwert (ein Skalar).

Instinct hinter Eigenvektoren

Stellen Sie sich vor, Sie haben eine Matrix A, die eine lineare Transformation darstellt, z. B. das Strecken, Drehen oder Skalieren eines zweidimensionalen Raums. Wenn diese Transformation auf einen Vektor v angewendet wird:

• Die meisten Vektoren ändern ihre Richtung und Größe.
• Einige spezielle Vektoren werden jedoch nur skaliert, aber nicht gedreht oder gespiegelt. Diese speziellen Vektoren sind Eigenvektoren.

Zum Beispiel:

• Wenn λ>1, ist der Eigenvektor gestreckt.
• Wenn 0<λ<1, wird der Eigenvektor komprimiert.
• Wenn λ=−1, kehrt der Eigenvektor seine Richtung um, behält aber die gleiche Länge bei.

Warum sind Eigenvektoren wichtig?

Eigenvektoren spielen in verschiedenen mathematischen und realen Anwendungen eine entscheidende Rolle:

1. Hauptkomponentenanalyse (PCA): PCA ist eine weit verbreitete Technik zur Dimensionsreduktion. Eigenvektoren werden verwendet, um die Hauptkomponenten der Daten zu bestimmen, die die maximale Varianz erfassen und dabei helfen, die wichtigsten Merkmale zu identifizieren.
2. Google PageRank: Der Algorithmus zur Rangfolge von Webseiten verwendet Eigenvektoren einer Matrix, die die Hyperlinks zwischen Webseiten darstellt. Der Haupteigenvektor hilft bei der Bestimmung der relativen Bedeutung jeder Seite.
3. Quantenmechanik: In der Physik beschreiben Eigenvektoren und Eigenwerte die Zustände eines Methods und ihre messbaren Eigenschaften, beispielsweise Energieniveaus.
4. Laptop Imaginative and prescient: Eigenvektoren werden in Gesichtserkennungssystemen verwendet, insbesondere in Techniken wie Eigenfaces, wo sie dabei helfen, Bilder als lineare Kombinationen signifikanter Merkmale darzustellen.
5. Schwingungsanalyse: Im Ingenieurwesen beschreiben Eigenvektoren die Schwingungsmodi in Bauwerken wie Brücken und Gebäuden.

Wie berechnet man Eigenvektoren?

Um Eigenvektoren zu finden, gehen Sie folgendermaßen vor:

• Stellen Sie die Eigenwertgleichung auf: Beginnen Sie mit Av=λv und schreiben Sie es um als (A−λI)v=0, wobei I die Identitätsmatrix ist. Nach Eigenwerten auflösen: Eigenvektoren finden:
• Nach Eigenwerten auflösen: Berechnen Sie det⁡(A−λI)=0, um die Eigenwerte λ zu finden.
• Finden Sie Eigenvektoren: Ersetzen Sie jeden Eigenwert λ durch (A−λI)v=0 und lösen Sie nach v auf.

Beispiel: Eigenvektoren in Aktion

Betrachten Sie eine Matrix:

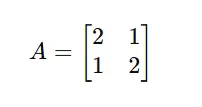
Schritt 1: Finden Sie die Eigenwerte λ.

Lösen Sie det⁡(A−λI)=0:

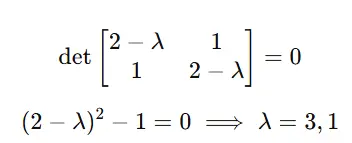
Schritt 2: Finden Sie Eigenvektoren für jedes λ.

Für λ=3:

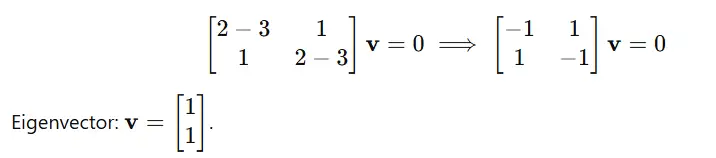
Für λ=1:

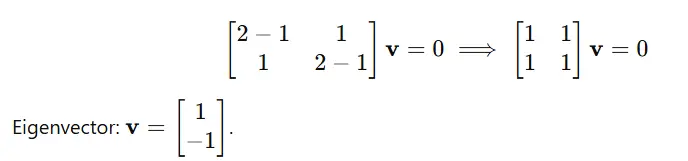
Python-Implementierung

Berechnen wir die Eigenwerte und Eigenvektoren einer Matrix mit Python.

Beispielmatrix

Betrachten Sie die Matrix:

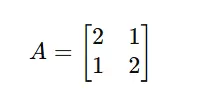
Code-Implementierung

import numpy as np

# Outline the matrix
A = np.array(((2, 1), (1, 2)))

# Compute eigenvalues and eigenvectors
eigenvalues, eigenvectors = np.linalg.eig(A)

# Show outcomes
print("Matrix A:")
print(A)

print("nEigenvalues:")
print(eigenvalues)

print("nEigenvectors:")
print(eigenvectors)

Ausgabe:

Matrix A:
((2 1)
 (1 2))

Eigenvalues:
(3. 1.)

Eigenvectors:
(( 0.70710678 -0.70710678)
 ( 0.70710678  0.70710678))

Eigenvektoren visualisieren

Sie können visualisieren, wie sich Eigenvektoren unter der durch Matrix A definierten Transformation verhalten.

Visualisierungscode

import matplotlib.pyplot as plt

# Outline eigenvectors
eig_vec1 = eigenvectors(:, 0)
eig_vec2 = eigenvectors(:, 1)

# Plot unique eigenvectors
plt.quiver(0, 0, eig_vec1(0), eig_vec1(1), angles="xy", scale_units="xy", scale=1, coloration="r", label="Eigenvector 1")
plt.quiver(0, 0, eig_vec2(0), eig_vec2(1), angles="xy", scale_units="xy", scale=1, coloration="b", label="Eigenvector 2")

# Modify plot settings
plt.xlim(-1, 1)
plt.ylim(-1, 1)
plt.axhline(0, coloration="grey", linewidth=0.5)
plt.axvline(0, coloration="grey", linewidth=0.5)
plt.grid(coloration="lightgray", linestyle="--", linewidth=0.5)
plt.legend()
plt.title("Eigenvectors of Matrix A")
plt.present()

Mit diesem Code wird ein Diagramm erstellt, das die Eigenvektoren von AAA zeigt und deren Richtung sowie die Artwork und Weise, wie sie bei der Transformation unverändert bleiben, veranschaulicht.

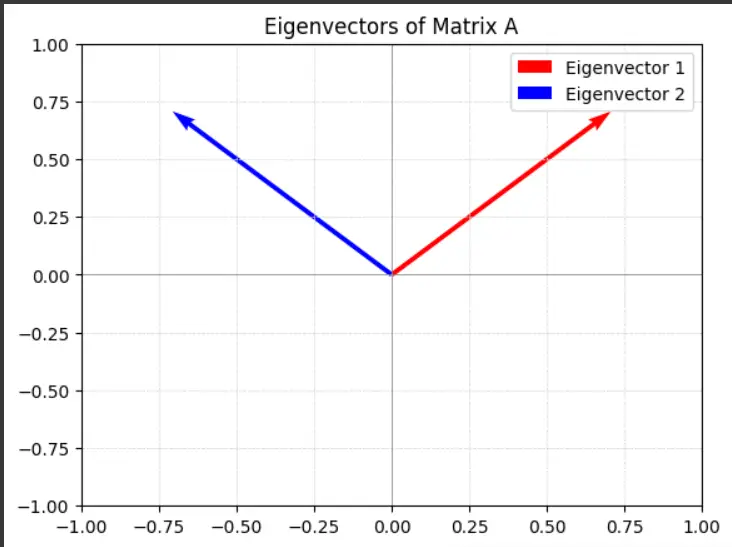
Wichtige Erkenntnisse

• Eigenvektoren sind spezielle Vektoren, die bei Transformation durch eine Matrix in derselben Richtung bleiben.
• Sie werden mit Eigenwerten gepaart, die bestimmen, wie stark die Eigenvektoren skaliert werden.
• Eigenvektoren finden bedeutende Anwendungen in den Bereichen Datenwissenschaft, maschinelles Lernen, Ingenieurwesen und Physik.
• Python bietet Instruments wie NumPy zur einfachen Berechnung von Eigenwerten und Eigenvektoren.

Abschluss

Eigenvektoren sind ein Grundkonzept in lineare Algebramit weitreichenden Anwendungen in den Bereichen Datenwissenschaft, Ingenieurwesen, Physik und darüber hinaus. Sie stellen die Essenz dar, wie sich eine Matrixtransformation auf bestimmte spezielle Richtungen auswirkt, was sie in Bereichen wie Dimensionsreduzierung, Bildverarbeitung und Schwingungsanalyse unverzichtbar macht.

Durch das Verstehen und Berechnen von Eigenvektoren erschließen Sie ein leistungsstarkes mathematisches Werkzeug, mit dem Sie komplexe Probleme klar und präzise lösen können. Mit Pythons robusten Bibliotheken wie NumPywird die Untersuchung von Eigenvektoren zum Kinderspiel, sodass Sie diese Konzepte visualisieren und in realen Szenarien anwenden können.

Ob Sie bauen Modelle für maschinelles LernenOb Sie nun die Strukturdynamik analysieren oder in die Quantenmechanik eintauchen – ein solides Verständnis der Eigenvektoren ist eine Fähigkeit, die Ihnen auf Ihrem Weg von großem Nutzen sein wird.

Häufig gestellte Fragen

Hallo, ich bin Janvi, ein leidenschaftlicher Knowledge-Science-Fanatic, der derzeit bei Analytics Vidhya arbeitet. Meine Reise in die Welt der Daten begann mit einer tiefen Neugier, wie wir aus komplexen Datensätzen aussagekräftige Erkenntnisse gewinnen können.