Was ist Tensor?

Einführung

Angenommen, Sie sind an einem anspruchsvollen Projekt beteiligt, beispielsweise an der Simulation realer Phänomene oder der Entwicklung eines fortgeschrittenen neurales Netzwerk um Wettermuster vorherzusagen. Tensoren sind komplexe mathematische Einheiten, die im Hintergrund arbeiten und diese anspruchsvollen Berechnungen ermöglichen. Tensoren verarbeiten mehrdimensionale Daten effizient und machen so solche innovativen Projekte möglich. Dieser Artikel soll den Lesern ein umfassendes Verständnis von Tensoren, ihren Eigenschaften und Anwendungen vermitteln. Als Forscher, Fachmann oder Pupil hilft Ihnen ein solides Verständnis von Tensoren beim Umgang mit komplexen Daten und fortgeschrittenen Computermodellen.

Überblick

• Definieren Sie, was ein Tensor ist, und verstehen Sie seine verschiedenen Formen und Dimensionen.
• Erkennen Sie die mit Tensoren verbundenen Eigenschaften und Operationen.
• Wenden Sie Tensorkonzepte in verschiedenen Bereichen wie Physik und maschinelles Lernen an.
• Führen Sie grundlegende Tensoroperationen und Transformationen mit Python durch.
• Verstehen Sie die praktischen Anwendungen von Tensoren in neuronalen Netzwerken.

Was ist Tensor?

Mathematisch gesehen sind Tensoren Objekte, die Matrizen, Vektoren und Skalare auf höhere Dimensionen erweitern. Die Bereiche Informatik, Ingenieurwesen und Physik sind alle stark von Tensoren abhängig, insbesondere wenn es um tiefes Lernen Und maschinelles Lernen.

Ein Tensor ist, vereinfacht ausgedrückt, eine Reihe von Zahlen mit möglichen Dimensionen. Der Rang des Tensors ist die Anzahl der Dimensionen. Hier eine Erklärung:

• Skalar: Eine einzelne Zahl (Tensor vom Rang 0).
• Vektor: Ein eindimensionales Array von Zahlen (Tensor mit Rang 1).
• Matrix: Ein zweidimensionales Array von Zahlen (Tensor vom Rang 2).
• Tensoren höherer Ordnung: Arrays mit drei oder mehr Dimensionen (Rang 3 oder höher).

Mathematisch lässt sich ein Tensor wie folgt darstellen:

• Ein Skalar (s) kann als (s) bezeichnet werden.
• Ein Vektor (v) kann als (v_i) bezeichnet werden, wobei (i) ein Index ist.
• Eine Matrix (M) kann als (M_{ij}) bezeichnet werden, wobei (i) und (j) Indizes sind.
• Ein Tensor höheren Ranges ( T ) kann als ( T_{ijk…} ) bezeichnet werden, wobei ( i, j, okay, ) usw. Indizes sind.

Eigenschaften von Tensoren

Tensoren verfügen über mehrere Eigenschaften, die sie zu vielseitigen und leistungsstarken Werkzeugen in verschiedenen Bereichen machen:

• Abmessungen: Die Anzahl der Indizes, die zur Beschreibung des Tensors erforderlich sind.
• Rangordnung): Die Anzahl der Dimensionen eines Tensors.
• Kind: Die Größe jeder Dimension. Beispielsweise hat ein Tensor mit der Kind (3, 4, 5) die Dimensionen 3, 4 und 5.
• Typ: Tensoren können verschiedene Datentypen enthalten, z. B. ganze Zahlen, Gleitkommazahlen usw.

Tensoren in der Mathematik

In der Mathematik verallgemeinern Tensoren Konzepte wie Skalare, Vektoren und Matrizen zu komplexeren Strukturen. Sie sind in verschiedenen Bereichen von der linearen Algebra bis zur Differentialgeometrie von entscheidender Bedeutung.

Beispiel für Skalare und Vektoren

• Skalar: Eine einzelne Zahl. Beispielsweise kann die Temperatur an einem Punkt im Raum als Skalarwert dargestellt werden, etwa ( s = 37 ) Grad Celsius.
• Vektor: Ein numerisches Array mit Größe und Richtung in einer Dimension. Beispielsweise kann ein Vektor (v = (3, 4, 5)) verwendet werden, um die Geschwindigkeit eines bewegten Objekts zu beschreiben, wobei jedes Factor die Geschwindigkeitskomponente in einer bestimmten Richtung darstellt.

Beispiel für Tensoren in der linearen Algebra

Betrachten Sie eine Matrix ( M ), die ein zweidimensionaler Tensor ist:

Mehrdimensionale Daten, wie etwa ein Bild mit drei Farbkanälen, können durch komplexe Tensoren wie Rang-3-Tensoren dargestellt werden, während die Matrix für Transformationen wie Rotation oder Skalierung von Vektoren in einer Ebene verwendet wird. Dimensionen beziehen sich auf Farbtiefe, Breite und Höhe.

Beispiel einer Tensorkontraktion

Die Tensorkontraktion ist eine Verallgemeinerung der Matrixmultiplikation. Wenn wir beispielsweise zwei Matrizen ( A ) und ( B ) haben:

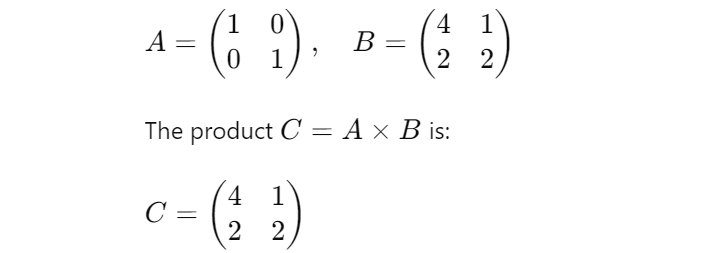
Hier werden die Indizes von (A) und (B) summiert, um die Elemente von (C) zu erzeugen. Dieses Konzept lässt sich auf Tensoren höheren Ranges erweitern und ermöglicht komplexe Transformationen und Operationen in mehrdimensionalen Räumen.

Tensoren in der Informatik und im maschinellen Lernen

Tensoren sind von entscheidender Bedeutung für die Organisation und Analyse mehrdimensionaler Daten in der Informatik und im maschinellen Lernen, insbesondere in Deep-Studying-Frameworks wie PyTorch und TensorFlow.

Daten Präsentation

Tensoren werden zur Darstellung verschiedener Datenformen verwendet:

• Skalare: Dargestellt als Tensoren mit Rang 0. Beispielsweise ein einzelner numerischer Wert, wie eine Lernrate in einem maschinellen Lernalgorithmus.
• Vektoren: Dargestellt als Tensoren der Stufe 1. Beispielsweise eine Liste von Merkmalen für einen Datenpunkt, wie etwa Pixelintensitäten in einem Graustufenbild.
• Matrizen: Als Tensordarstellungen mit Rang 2. Wird häufig verwendet, um Datensätze zu speichern, in denen ein Merkmal durch eine Spalte und eine Datenprobe durch eine Zeile dargestellt wird.
• Tensoren höherer Ordnung: Wird mit komplexeren Datenformaten verwendet. Beispielsweise kann ein Tensor der Stufe 3 mit den Dimensionen (Höhe, Breite, Kanäle) zur Darstellung eines Farbbilds verwendet werden.

Tensoren im Deep Studying

Beim Deep Studying werden Tensoren zur Darstellung folgender Dinge verwendet:

• Eingabedaten: In das neuronale Netzwerk eingespeiste Rohdaten. Beispielsweise kann ein Stapel von Bildern als 4-dimensionaler Tensor mit Kind (Stapelgröße, Höhe, Breite, Kanäle) dargestellt werden.
• Gewichte und Verzerrungen: Parameter des neuronalen Netzwerks, die während des Trainings gelernt werden. Diese werden ebenfalls als Tensoren geeigneter Formen dargestellt.
• Zwischenaktivierungen: Ausgaben jeder Schicht im neuronalen Netzwerk, die ebenfalls Tensoren sind.

Beispiel

Betrachten Sie ein einfaches neuronales Netzwerk mit einer Eingabeschicht, einer verborgenen Schicht und einer Ausgabeschicht. Die Daten und Parameter in jeder Schicht werden als Tensoren dargestellt:

import torch

# Enter information: batch of two photos, every 3x3 pixels with 3 coloration channels (RGB)
input_data = torch.tensor(((((1, 2, 3), (4, 5, 6), (7, 8, 9)),
                            ((9, 8, 7), (6, 5, 4), (3, 2, 1)),
                            ((0, 0, 0), (1, 1, 1), (2, 2, 2))),
                           (((2, 3, 4), (5, 6, 7), (8, 9, 0)),
                            ((0, 9, 8), (7, 6, 5), (4, 3, 2)),
                            ((1, 2, 3), (4, 5, 6), (7, 8, 9)))))

# Weights for a layer: assuming a easy absolutely related layer
weights = torch.rand((3, 3, 3, 3))  # Random weights for demonstration

# Output after making use of weights (simplified)
output_data = torch.matmul(input_data, weights)

print(output_data.form)
# Output: torch.Measurement((2, 3, 3, 3))

Hier sind input_data ein Tensor der Stufe 4, der einen Stapel von zwei 3×3 RGB-Bildern darstellt. Die Gewichte werden ebenfalls als Tensor dargestellt, und die Ausgabedaten nach dem Anwenden der Gewichte sind ein weiterer Tensor.

Tensoroperationen

Zu den üblichen Operationen an Tensoren gehören:

• Elementweise Operationen: Operationen, die unabhängig auf jedes Factor angewendet werden, wie z. B. Addition und Multiplikation.
• Matrix-Multiplikation: Ein Sonderfall der Tensorkontraktion, bei dem zwei Matrizen multipliziert werden, um eine dritte Matrix zu erzeugen.
• Umformung: Ändern der Kind eines Tensors, ohne seine Daten zu verändern.
• Umsetzung: Vertauschen der Dimensionen eines Tensors.

Darstellung eines 3×3 RGB-Bildes als Tensor

Betrachten wir ein praktisches Beispiel aus dem maschinellen Lernen. Angenommen, wir haben ein Bild, das als dreidimensionaler Tensor mit Kind (Höhe, Breite, Kanäle) dargestellt wird. Bei einem Farbbild sind die Kanäle normalerweise Rot, Grün und Blau (RGB).

# Create a 3x3 RGB picture tensor
picture = np.array((((255, 0, 0), (0, 255, 0), (0, 0, 255)),
                  ((255, 255, 0), (0, 255, 255), (255, 0, 255)),
                  ((128, 128, 128), (64, 64, 64), (32, 32, 32))))

print(picture.form)

Hier ist das Bild ein Tensor mit der Kind (3, 3, 3), der ein 3×3-Bild mit 3 Farbkanälen darstellt.

Implementierung eines einfachen CNN zur Bildklassifizierung

In einem Convolutional Neural Community (CNN), das zur Bildklassifizierung verwendet wird, wird ein Eingabebild als Tensor dargestellt und durch mehrere Schichten geleitet, von denen jede den Tensor mithilfe von Operationen wie Faltung und Pooling transformiert. Der endgültige Ausgabetensor stellt die Wahrscheinlichkeiten verschiedener Klassen dar.

import torch
import torch.nn as nn
import torch.nn.useful as F  # Importing the useful module
# Outline a easy convolutional neural community
class SimpleCNN(nn.Module):
   def __init__(self):
       tremendous(SimpleCNN, self).__init__()
       self.conv1 = nn.Conv2d(in_channels=1, out_channels=16, kernel_size=3)
       self.pool = nn.MaxPool2d(kernel_size=2, stride=2)
       self.fc1 = nn.Linear(16 * 3 * 3, 10)
   def ahead(self, x):
       x = self.pool(F.relu(self.conv1(x)))  # Utilizing F.relu from the useful module
       x = x.view(-1, 16 * 3 * 3)
       x = self.fc1(x)
       return x
# Create an occasion of the community
mannequin = SimpleCNN()
# Dummy enter information (e.g., a batch of 1 grayscale picture of dimension 8x8)
input_data = torch.randn(1, 1, 8, 8)
# Ahead cross
output = mannequin(input_data)
print(output.form)

Ein Stapel von Fotos wird in diesem Beispiel durch den Tensor input_data der Stufe 4 dargestellt. Diese Tensoren werden von den Faltungs- und vollständig verbundenen Schichten verarbeitet, die verschiedene Operationen auf sie anwenden, um das gewünschte Ergebnis zu erzielen.

Abschluss

Tensoren sind mathematische Strukturen, die Matrizen, Vektoren und Skalare in höhere Dimensionen bringen. Sie sind unter anderem für die theoretische Physik und das maschinelle Lernen von entscheidender Bedeutung. Fachleute, die im Bereich Deep Studying und künstliche Intelligenz arbeiten, müssen Tensoren verstehen, um moderne Rechenrahmen zur Weiterentwicklung von Forschung, Ingenieurwesen und Technologie nutzen zu können.

Häufig gestellte Fragen