Mein Wirtschaftskollege aus Columbia schreibt:
Die folgende Abbildung zeigt, wie sich die Siegeswahrscheinlichkeit der beiden Kandidaten der großen Parteien seit dem 6. August – dem Tag, nachdem Kamala Harris offiziell die Nominierung ihrer Partei erhielt – gemäß drei statistischen Modellen entwickelt hat (Trump in Rot, Harris in Blau):
Die vom Markt abgeleiteten Wahrscheinlichkeiten schwankten innerhalb einer engeren Bandbreite. Die folgende Abbildung zeigt die Preise für Verträge, die einen Greenback auszahlen, wenn Harris die Wahl gewinnt, und sonst nichts, basierend auf Daten von zwei Prognosemärkten (die Preise wurden leicht angepasst, um die Interpretation als Wahrscheinlichkeiten zu erleichtern, und die vertikalen Achsen wurden denen der Modelle angepasst):
Derzeit liegen uns additionally fünf verschiedene Antworten auf dieselbe Frage vor. Die Wahrscheinlichkeit, dass Harris sich durchsetzen wird, liegt laut diesen Quellen zwischen 51 und 60 Prozent. An manchen Tagen battle die Spanne der Uneinigkeit sogar doppelt so groß.
Wie wir besprochen habenein Unterschied von 10 % der vorhergesagten Wahrscheinlichkeit entspricht etwa einem Unterschied von 0,4 % (additionally 0,004) beim vorhergesagten Stimmenanteil. Additionally, ja, es macht für mich absolut Sinn, dass verschiedene seriöse Prognosen so stark voneinander abweichen, und es macht auch Sinn, dass die Märkte so stark voneinander abweichen können. (Wie Rajiv in einem früheren Beitrag erörtert hat, ist es aus logistischen Gründen nicht einfach, zwischen den beiden oben gezeigten Märkten Arbitrage zu betreiben, sodass es möglich ist, dass sie einen gewissen Abstand zwischen ihnen wahren.)
Das ist zwar nur eine Kleinigkeit, aber wenn Sie zwei Linien zeichnen möchten, die sich zu einer Konstanten addieren, reicht es aus, nur eine davon zu zeichnen. Ich sage das teilweise aus allgemeinen Gründen und teilweise, weil diese Linien, die 0,5 kreuzen, Formen und andere visuelle Artefakte erzeugen, wie die „Vase“ im PredictIt-Diagramm. Ich denke, diese visuellen Artefakte behindern das Betrachten und Lernen aus den Daten.
OK, das ist alles Hintergrundwissen. Verschiedene Prognosen unterscheiden sich. Normalerweise bewerten wir Prognosen, indem wir sie mit den Ergebnissen vergleichen. Rajiv schreibt:
Der Standardansatz würde darin bestehen, zu warten, bis das Ergebnis bekannt gegeben wird, und dann einen Fehlermaßstab zu berechnen, beispielsweise den durchschnittlichen täglichen Brier-Rating. Dies kann und wird nicht nur für den Gewinner der Präsidentschaftswahlen getan, sondern auch für die Ergebnisse in jedem umkämpften Staat, den Gewinner der Volksabstimmung und verschiedene Szenarien im Wahlkollegium.
Ich denke, die Bewertung sollte auf Grundlage der Stimmendifferenz erfolgen und nicht auf Grundlage des binären Gewinn-/Verlustergebnisses, da die Bewertung auf Grundlage eines binären Ergebnisses hoffnungslos ungenau ist, ein Punkt, der in diesem Weblog schon oft angesprochen wurde und den ich nochmal erklärt letzten Monat. Aber selbst wenn Sie den Stimmenunterschied berücksichtigen, haben Sie immer noch nur ein Wahlergebnis und das wird Ihnen nicht ausreichen, um verschiedene vernünftige Prognosen zu vergleichen.
Rajiv hat eine neue Idee:
Es gibt jedoch eine Methode, mit der man bereits vor der Realisierung des Ereignisses ein vorläufiges Maß für die Prognoseleistung erhalten kann. Die Grundidee ist folgende: Stellen Sie sich einen Händler vor, der an ein bestimmtes Modell glaubt und auf der Grundlage dieser Überzeugung an einem der Märkte handelt. Ein solcher Händler wird Kontrakte kaufen und verkaufen, wenn sich entweder die Modellprognose oder der Marktpreis ändert, und er wird eine Place halten, die größer sein wird, wenn die Differenz zwischen der Prognose und dem Preis selbst größer ist. Diese Handelsaktivität wird zu einem sich entwickelnden Portfolio führen, das nach jeder Modellaktualisierung neu gewichtet wird. Man kann den Wert des resultierenden Portfolios an einem beliebigen Tag betrachten, den kumulierten Gewinn oder Verlust im Laufe der Zeit berechnen und die Rendite als Maß für die Prognosegenauigkeit bis zum aktuellen Zeitpunkt verwenden.
Dies kann für jedes Modell-Markt-Paar und sogar für Modellpaare oder Marktpaare durchgeführt werden (indem eine Prognose als Preis interpretiert wird oder umgekehrt).
Ich bin nicht mit allem einverstanden, was Rajiv hier tut. Er schreibt: „Der Händler battle zu Beginn mit 1.000 US-Greenback und ohne Verträge ausgestattet und ihm wurden Präferenzen hinsichtlich des Endvermögens zugewiesen, die sich nach dem Log-Nutzen richteten (um ein gewisses Maß an Risikoaversion zu ermöglichen).“ Das ergibt für mich keinen Sinn, da ich glaube, dass jeder, der 1.000 US-Greenback in einen Prognosemarkt investiert, alles verlieren könnte, ohne viel davon zu spüren. Aber ich vermute, dass sich an den grundlegenden Ergebnissen nichts ändern würde, wenn die Analyse auf ein sinnvolleres lineares Nutzenmodell umgestellt würde.
Rajiv fasst seine empirischen Ergebnisse zusammen:
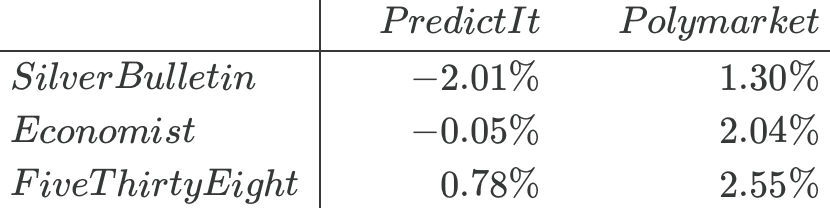
Wenn wir diese Übung für jedes Modell-Markt-Paar wiederholen, erhalten wir die folgenden Renditen:
Unter den Modellen schneidet FiveThirtyEight am besten und Silver Bulletin am schlechtesten gegenüber jedem der beiden Märkte ab, obwohl die Unterschiede nicht groß sind. Und unter den Märkten ist PredictIt schwerer zu schlagen als Polymarket.
Ich betrachte dies nicht als sinnvolle Auswertung der drei öffentlichen Prognosen, weil … das sind kleine Zahlen und es ist immer noch nur N = 1. Wir sprechen hier von einer Kampagne. Anders ausgedrückt: Wie hoch sind die Standardfehler dieser Zahlen? Aus nur einem Datenpunkt kann man keinen Standardfehler ableiten.
Dies bedeutet nicht, dass die Idee inhaltsleer ist; wir sollten lediglich eine Überinterpretation der Ergebnisse vermeiden.
Ich habe Rajivs Idee noch nicht vollständig verarbeitet, aber ich denke, sie hängt mit der Martingaleigenschaft kohärenter probabilistischer Prognosen zusammen, wie wir sie im Zusammenhang mit Wetten auf School-Basketball Und Wahlen.
Wie man es auch dreht und wendet, Ihre Zeitreihenprognosen werden durch eine zu große Volatilität zunichte gemacht: Wenn Sie davon ausgehen, dass Sie einen Fluss von Informationen mit Störsignalen einbeziehen müssen, müssen Sie Ihre Prognosen (mithilfe einer „Voraussage“ oder eines „Modells“) verankern, um zu verhindern, dass Ihre Prognose durch Störsignale verfälscht wird.
Leider steht dieses Ziel einer vernünftig kalibrierten Stabilität im Widerspruch zu einem anderen Ziel der öffentlichen Wettervorhersager: nämlich Aufmerksamkeit zu erregen! Dafür wollen Sie, dass Ihre Prognosen ständig schwanken, damit Sie weiterhin Nachrichten liefern.
Ich habe das Obige an Rajiv geschickt, der schrieb:
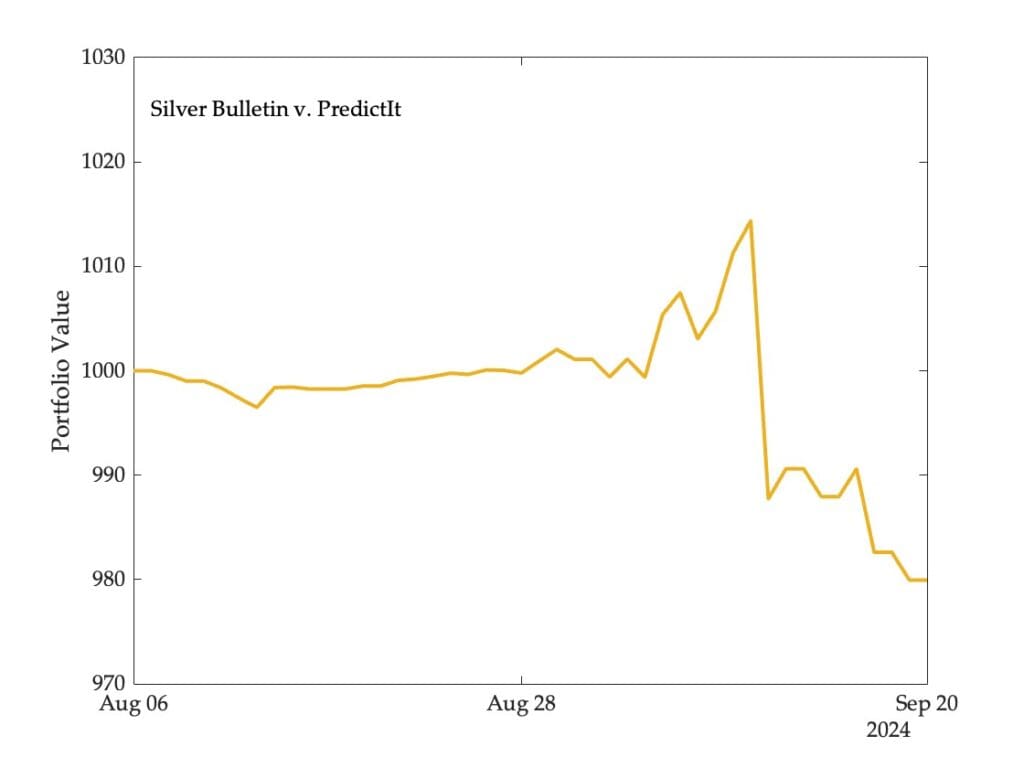
Eine Sache, die ich in dem Beitrag nicht gezeigt habe, ist, wie sich der Wert des Portfolios (Handel auf PredictIt) im Laufe der Zeit entwickelt hätte:
Sie werden sehen, dass Silver Bulletin intestine abgeschnitten hätte, wenn ich diese Analyse vor ein paar Wochen durchgeführt hätte. Als der Preis des Harris-Kontrakts auf den Märkten stieg, litt das Unternehmen wirklich, da es eine erhebliche Quick-Place hielt.
Die Lehre daraus (denke ich) ist, dass wir viele Ereignisse brauchen, um zu einer Schlussfolgerung zu gelangen. Ich arbeite an Prognosen für die Gewinner auf Landesebene und auf Foundation der Mehrheitswahl, aber natürlich werden diese alle korreliert sein, sodass sie bei dem Drawback der geringen Anzahl von Ereignissen nicht wirklich helfen. Das ist der Grimmer-Knox-Westwood-Punkt, wie ich ihn verstehe.
Wenn wir dieses Verfahren rückwirkend auf vergangene Zeitreihen von Prognosen oder Wettmärkten anwenden würden, die zu variabel waren, weil sie sich zu sehr an den Umfragen orientierten, dann könnte es meiner Meinung nach/hoffentlich die Probleme aufdecken. Nach 2016 haben die Prognostiker hart daran gearbeitet, ihre Prognosen mit viel Unsicherheit zu belassen, und ich denke, dass ein Ergebnis davon darin besteht, die Marktpreise stabiler zu halten.