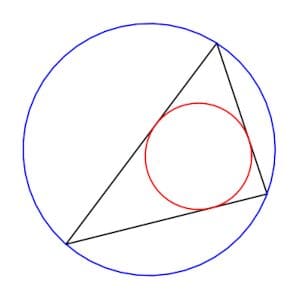
Sei a, b und c die Seiten eines Dreiecks.
Sei p Umfang des Dreiecks.
Sei r der Radius des größten Kreises, der in das Dreieck eingeschrieben werden kann, und sei der Radius des Kreises durch die Scheitelpunkte des Dreiecks.
Dann können alle sechs Zahlen in einer Gleichung zusammenhängen:
2Prr = ABC.
Das ist nur verrückt und ich habe keine Instinct für diese Artwork von Geometrieproblem. Mathematik ist komisch. Ich kann die Dimensionalitätsanalyse verwenden, um zu überprüfen, ob es nicht unbedingt falsch ist, und ich könnte ein einfaches Beispiel mit einem gleichseitigen Dreieck herausfinden, um zu überprüfen, ob es für einen Sonderfall funktioniert, aber ich habe keine Instinct, dass die Formel im Allgemeinen funktionieren würde.
Ich gehe davon aus, dass ich die obige Aussage mit kartesischen Brute-Drive-Koordinaten beweisen könnte: Beschriften Sie die Punkte als (x, y) _i, i = 1,2,3, dann ist der Umfang sqrt ((x1-x2)^2 + (y1-y2)^2) + sqrt ((x2-x3)^2 + (y2-y3)^2) + (Y3-y1)^2), und es gibt Formeln für die Zentren der roten und blauen Kreise im obigen Bild, und dann ist es einfach genug, die Formeln für R und R zu schreiben, und dann schätze ich, dass, wenn man die Faktoren multipliziert und die Dinge in der einen oder anderen Weise neu ordnet, alles funktioniert. Angesichts der Tatsache, dass die Aussage wahr ist, muss sie funktionieren, oder?
Ich vermute auch, dass es eine gewisse Instinct gibt, dies zu erklären, eine klare Ableitung.
Mein Punkt bei der Veröffentlichung dessen liegt nicht daran, dass es mir um Dreiecke interessiert ist. Vielmehr möchte ich nur mit Ihnen teilen, wie wenig Verständnis ich von diesem Bereich der Mathematik habe. Wenn es um Wahrscheinlichkeit und Statistik geht, habe ich viel Instinct. Nicht, dass meine Instinct immer richtig ist, ich habe nur einen Rahmen für die Nachdenken über Wahrscheinlichkeits- und Statistikprobleme, eine Kombination aus theoretischen Strukturen und Tausenden von Beispielen, über die ich über die Jahre nachgedacht und über das ich gearbeitet habe. Mit der Geometrie habe ich das nicht.
Diese Episode gibt mir eine gewisse Instinct, wie Schüler oft so wenig Einblick in Wahrscheinlichkeit und Statistik zeigen können. Die Schüler wissen, dass diese Themen wichtig sind; Sie haben einfach nicht die Erfahrung und Gedankengüter, die sie durch das Gesamtbild steuern können.
Experten (die ich in Wahrscheinlichkeit und Statistik bin, aber nicht in Geometrie, Zahlentheorie usw.) können kilometerweit sehen; Nicht-Experten laufen im hohen Gras herum und können nicht über ihren nächsten Schritt hinaus sehen.