Nach 12 Jahren haben wir endlich herausgefunden, wie man eine NUTS-ähnliche lokale Schrittweitenanpassung für NUTS durchführen kann, die die detaillierte Stability bewahrt. Dies beginnt mit Michael Betancourts überarbeitetem multinomialen NUTS, wie es in Stan verwendet wird, mit einer Tendenz zur letzten Verdoppelung.
Wir haben gerade das arXiv-Papier veröffentlicht und würden uns über Suggestions dazu freuen.
-
Nawaf Bou-Rabee, Bob Carpenter, Tore Selland Kleppe, Milo Marsden. 2024. Einbeziehung lokaler Schrittweitenadaption in den No-U-Flip-Sampler mithilfe der Gibbs-Selbstoptimierung. arXiv 2408.08259.
Nawaf hat gerade auf der Bernoulli-Konferenz in Deutschland einen Vortrag gehalten, in dem er unsere Arbeit zu GIST zusammenfasste, und ich habe im Juni bei Sam Livingstones Workshop in London einen Vortrag darüber gehalten.
Es klappt!
Hier ist ein Diagramm aus dem Dokument, das die Randwerte des Logarithmus-Skalenparameters von Neals Trichter sowohl in unserem neuen lokalen, schrittweise angepassten GIST als auch in Stans NUTS-Implementierung zeigt.
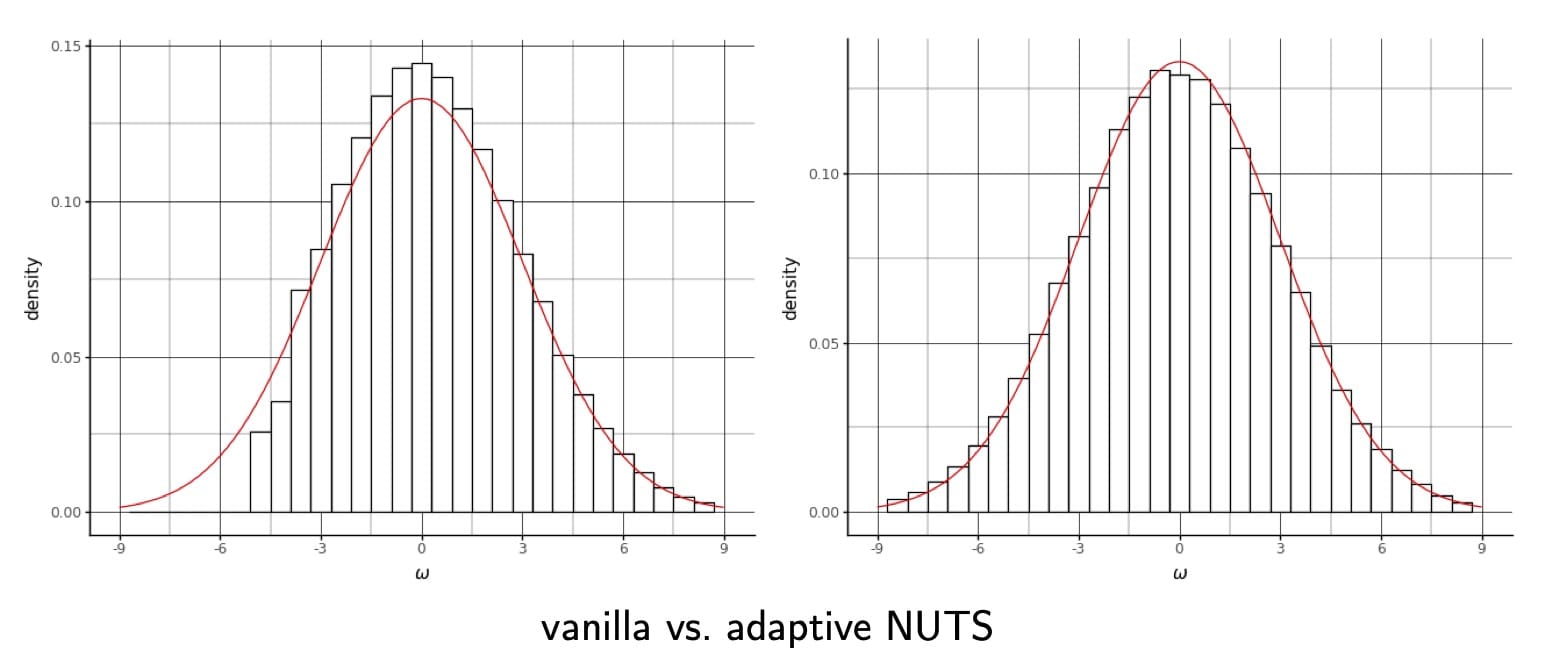
Beachten Sie, dass NUTS nicht in den Hals des Trichters gelangt, wo der Log-Skalenparameter niedrig ist. Dies wäre mit einer schattierten Histogrammfüllung leichter zu erkennen gewesen, daher sollten wir das für das überarbeitete Dokument beheben.
Die Idee hinter GIST
In GIST koppeln wir die Abstimmungsparameter (Schrittweite, Anzahl der Schritte, Massenmatrix) mit der Place und dem Impuls. Wir tun dies auf die gleiche Weise, wie HMC selbst den Impuls mit der Place gekoppelt hat. Konkret entwerfen wir eine bedingte Verteilung der Abstimmungsparameter bei gegebener Place und Impuls. Anschließend tasten wir die Abstimmungsparameter in einem Gibbs-Schritt neu ab, ähnlich wie wir den Impuls neu abtasten. Die Hamilton-Komponente (in diesem Fall NUTS) ist dann ein einfacher Metropolis-innerhalb-Gibbs-Schritt (wie in Vanilla HMC). Anders als in HMC, wo die Impulsverteilung unabhängig von der Positionsverteilung ist, haben wir in GIST eine Abhängigkeit zwischen den Abstimmungsparametern und der Place/dem Impuls, sodass wir einen nicht-trivialen Metropolis-Hastings-Schritt benötigen (anders als bei NUTS). Der Trick besteht darin, eine bedingte Verteilung der Abstimmungsparameter zu entwerfen, die die richtige lokale Anpassung vornimmt und zu einer hohen Akzeptanzrate führt – genau das zeigen die Artikel.
Es ist möglicherweise einfacher, mit dem ersten GIST-Artikel zu beginnen, der das Framework vorstellt und zeigt, dass NUTS, Apogäum-zu-Apogäum, randomisierte und multinomiale HMC als GIST-Sampler gestaltet werden können, und außerdem eine einfachere, auf U-Flip basierende Different zu NUTS vorstellt.
-
Nawaf Bou-Rabee, Bob Carpenter, Milo Marsden. 2024. GIST: Gibbs-Selbstoptimierung für lokal adaptives Hamilton-Monte-Carlo.arXiv 2404.15253.
Hat jemand eine Massenmatrixanpassung?
Ich verfüge über einen funktionierenden Proof-of-Idea, der eine lokale Massenmatrixanpassung durchführt, und obwohl dieser bei der Vorkonditionierung multivariater Normale nahezu perfekt funktioniert, ist es mir nicht gelungen, ihn bei der lokalen Vorkonditionierung nicht-log-konkaver Ziele wie Neals Trichter zum Laufen zu bringen.
Reproduzierbarer Code
Code zur Reproduktion der Ergebnisse aus dem Papier und auch für unsere laufenden Experimente ist in unserem öffentlichen GitHub-Repo verfügbar.
Verzögerte Ablehnung (generalisiert) HMC
Dies ist eine Fortsetzung einer anderen Arbeit, die ich mit Mitarbeitern hier am Flatiron Institute zur lokalen Schrittweitenanpassung unter Verwendung verzögerter Ablehnung für Hamiltonian Monte Carlo durchgeführt habe.
- Chirag Modi, Alex Barnett, Bob Carpenter. 2024. Hamilton-Monte-Carlo-Verfahren mit verzögerter Ablehnung für die Stichprobennahme bei Multiskalenverteilungen. Bayesianische Analyse 19(3).
Wir haben diese Arbeit kürzlich erweitert und verwenden verallgemeinertes HMC, das viel effizienter ist und eine „lokalere“ Anpassung der Schrittweite ermöglicht als das, was wir world in GIST und verzögertem Ablehnungs-HMC tun.
-
Gilad Turok, Chirag Modi, Bob Carpenter. 2024. Sampling aus Multiskalendichten mit verzögerter Ablehnung, verallgemeinertes Hamilton-Monte-Carlo-Verfahren. arXiv 2406.02741.
Chirag erweitert die DR-G-HMC-Arbeit mit GIST und einem effizienten L-BFGS-ähnlichen Ansatz zur Schätzung der Massenmatrix. Dies scheint besser zu funktionieren als das, was ich rein innerhalb von GIST versucht habe. Bleiben Sie dran!
Bewerber
Milo Marsdender einen Großteil seines Lebensunterhalts mit der Arbeit an den GIST-Artikeln verdient hat, ist ein Doktorand der angewandten Mathematik in Stanford, der dieses Jahr seinen Abschluss macht und auf der Suche nach einer Postdoc- oder Fakultätsstelle ist.
Gilad Turokder die Leitung des DR-G-HMC-Papiers übernahm, struggle ein Praktikant im Fach Angewandte Mathematik der Columbia College, der dieses Jahr als Forschungsanalytiker bei Flatiron blieb. Er möchte sich nächstes Jahr für ein Graduiertenstudium in Informatik/ML bewerben. Halten Sie Ausschau nach unserem Blackjax-Paket, das Agrawals und Domkes Ansatz zur Normalisierung des Fluss-VI mit realNVP implementiert.
