Wir haben heute über die Blockierung in Experimenten im Unterricht gesprochen, und ein Schüler fragte: „Wann sollten wir eine ungleiche Anzahl von Einheiten in den Behandlungs- und Kontrollgruppen haben?“
Ich antwortete, dass das einfachste Beispiel ist, wenn die Behandlung teuer ist. Sie könnten 10.000 Menschen in Ihrer Bevölkerung haben, aber nur genug Finances, um die Behandlung auf 100 Menschen anzuwenden, sodass 99% in der Kontrollgruppe liegen. In anderen Umgebungen kann die Behandlung störend sein, und Sie würden sie auch hier nur auf einen kleinen Teil der verfügbaren Einheiten anwenden.
Aber selbst wenn Kosten kein Downside sind und Sie nur die statistische Effizienz maximieren möchten, könnte es sinnvoll sein, den beiden Gruppen unterschiedliche Anzahl von Einheiten zuzuweisen.
Zum Beispiel habe ich angenommen, dass Ihre Ergebnisse unter der Behandlung viel variabler sind als die Kontrolle. Um die grundlegende Schätzung des Behandlungseffekts – das durchschnittliche Ergebnis in der Behandlungsgruppe, abzüglich des Durchschnitts unter den Kontrollen – möchten Sie dann mehr Behandlungsbeobachtungen für die höhere Varianz berücksichtigen.
Aber dann machte ich eine Pause. Ich struggle von Verwirrung beeindruckt.
Hier gibt es zwei Intuitionen, und sie gehen in entgegengesetzte Richtungen:
(1) Behandlungsbeobachtungen sind variabler als Kontrollen. Sie benötigen additionally mehr Behandlungsmessungen, um eine genaue Schätzung für die Behandlungsgruppe zu erhalten.
(2) Behandlungsbeobachtungen sind variabler als Kontrollen. Daher sind die Beobachtungen der Behandlungen knapper, und Sie sollten mehr von Ihrem Finances den qualitativ hochwertigen Kontrollmessungen widmen.
Ich hatte das Gefühl, dass die richtige Argumentation (1), nicht (2) struggle, aber ich struggle mir nicht sicher.
Wie habe ich das Downside gelöst?
Rohe Kraft.
Hier ist der R:
n <- 100
expt_sim <- perform(n, p=0.5, s_c=1, s_t=2){
n_c <- spherical((1-p)*n)
n_t <- spherical(p*n)
se_dif <- sqrt(s_c^2/n_c + s_t^2/n_t)
se_dif
}
curve(expt_sim(100, x), from=.01, to=.99,
xlab="Proportion of information within the remedy group",
ylab="se of estimated remedy impact",
foremost="Assuming sd of measurements isntwice as excessive for handled as for controls",
bty="l")
Und hier ist das Ergebnis:
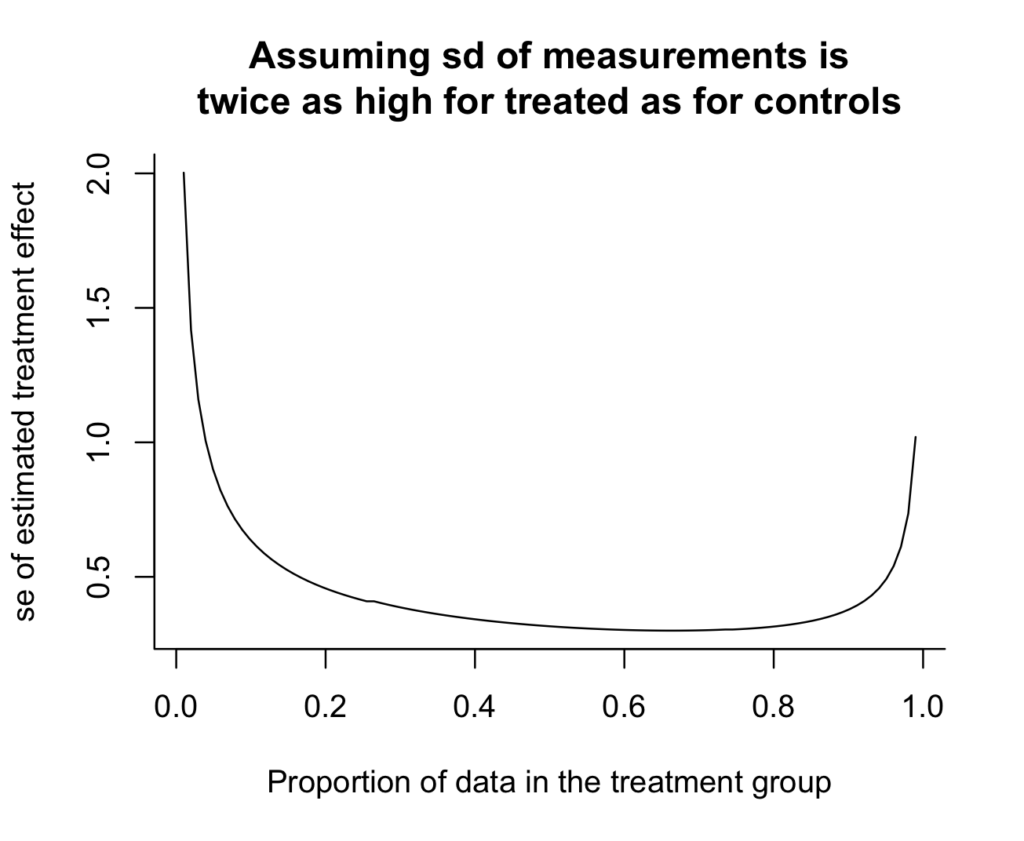
Oh, Shoot, ich magazine es wirklich nicht, wie die y-Achse nicht ganz auf Null geht. Es lässt die Varianzreduzierung dramatischer aussehen als es wirklich ist. Null ist in der NachbarschaftAdditionally luden wir es ein in:
curve(expt_sim(100, x), from=.01, to=.99, xlab="Proportion of information within the remedy group", ylab="se of estimated remedy impact", foremost="Assuming sd of measurements isntwice as excessive for handled as for controls", bty="l", xlim=c(0, 1), ylim=c(0, 2), xaxs="i", yaxs="i")

Und wir können die Antwort sehen: Wenn in der Behandlungsgruppe doppelt so viel Variation wie in der Kontrollgruppe vorliegt, sollten Sie in der Behandlungsgruppe doppelt so viele Messungen ergreifen. Die Kurve ist bei x = 2/3 minimiert (was wir überprüfen können, ohne etwas zu zeichnen, aber die Grafik bietet eine gewisse Instinct und eine Gesundheitsprüfung). Argument (1) oben ist korrekt.
Andererseits ist der Standardfehler aus dem optimalen Design nicht viel niedriger als das einfache 50/50 -Design, wie durch Berechnung des Verhältnisses ersichtlich ist:
print(expt_sim(100, 1/2) / expt_sim(100, 2/3))
das ergibt 0,95.
Somit ergibt das bessere Design eine Verringerung des Standardfehlers um 5%-das heißt, eine Effizienzgewinn von 10%. Nicht nichts, aber nicht riesig.
Wie auch immer, der Hauptpunkt dieses Beitrags ist, dass Sie viel aus der Simulation lernen können. After all on this case the issue could be solved analytically—just differentiate (s_c^2/(1-p) + s_t^2/p) with respect to p and set the by-product to zero, and also you get s_c^2/(1-p)^2 – s_t^2/p^2 = 0, thus s_c^2/(1-p)^2 = s_t^2/p^2, so p/(1-p) = s_t/s_c. Das ist alles in Ordnung, aber ich magazine die Brute-Power-Lösung.
