Kombination großer und kleiner LLMs zur Steigerung von Inferenzzeit und -qualität | von Richa Gadgil | Dez. 2024

Implementierung spekulativer und kontrastiver Dekodierung

Große Sprachmodelle bestehen aus Milliarden von Parametern (Gewichten). Für jedes Wort, das es generiert, muss das Modell rechenintensive Berechnungen für alle diese Parameter durchführen.

Große Sprachmodelle akzeptieren einen Satz oder eine Folge von Token und generieren eine Wahrscheinlichkeitsverteilung des nächstwahrscheinlichsten Tokens.

Daher typischerweise Dekodierung N Tokens (oder Generieren N Wörter aus dem Modell) erfordert die Ausführung des Modells N Anzahl der Male. Bei jeder Iteration wird das neue Token an den Eingabesatz angehängt und erneut an das Modell übergeben. Dies kann kostspielig sein.

Darüber hinaus kann die Dekodierungsstrategie die Qualität der generierten Wörter beeinflussen. Das einfache Generieren von Token, indem einfach das Token mit der höchsten Wahrscheinlichkeit in der Ausgabeverteilung verwendet wird, kann zu sich wiederholendem Textual content führen. Zufällige Stichproben aus der Verteilung können zu unbeabsichtigten Abweichungen führen.

Daher ist eine solide Dekodierungsstrategie erforderlich, um Folgendes sicherzustellen:

• Hochwertige Ergebnisse
• Schnelle Inferenzzeit

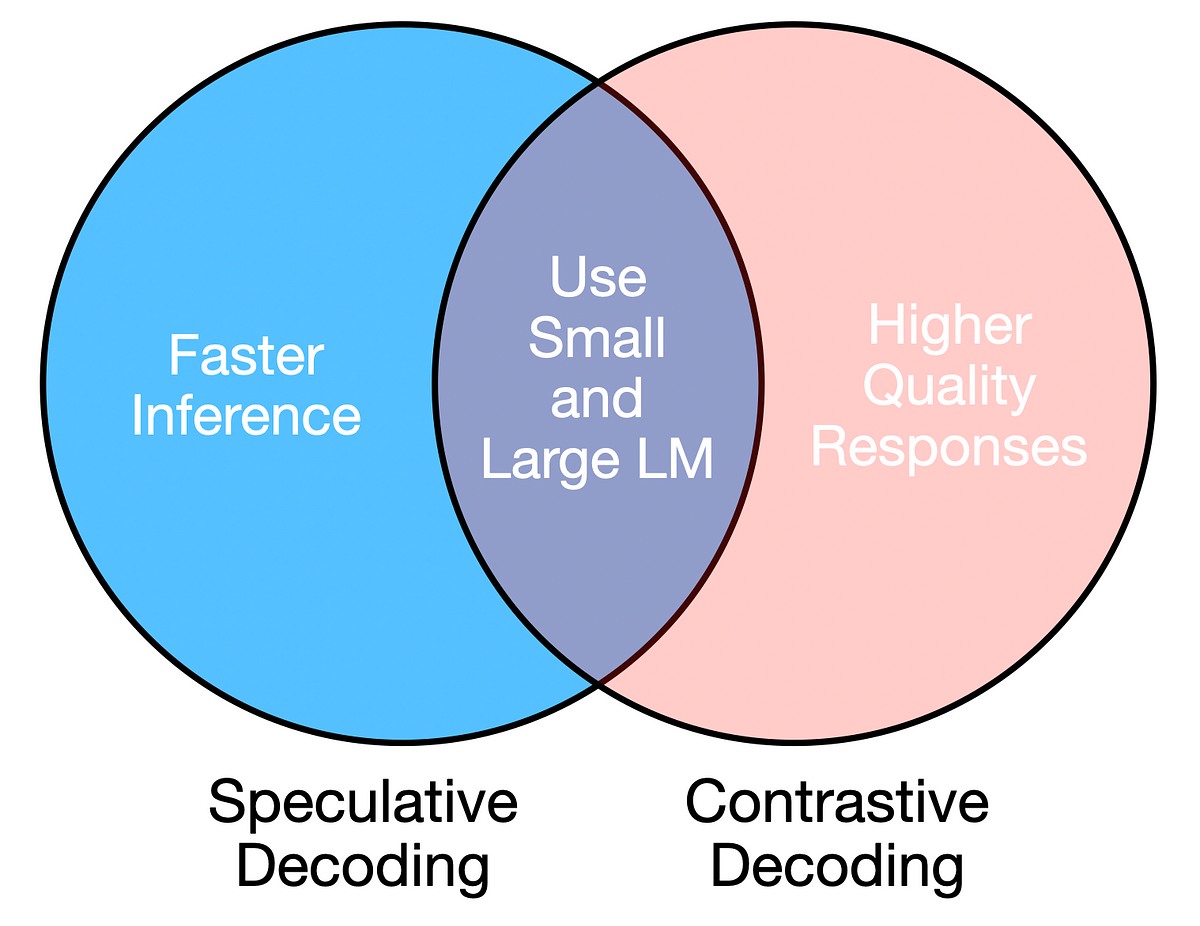
Beide Anforderungen können durch die Verwendung einer Kombination aus einem großen und einem kleinen Sprachmodell erfüllt werden, sofern die Novice- und Expertenmodelle ähnlich sind (z. B. gleiche Architektur, aber unterschiedliche Größen).

• Ziel/Großes Modell: Haupt-LM mit größerer Anzahl an Parametern (z. B. OPT-13B)
• Novice-/Kleinmodell: Kleinere Model des Principal LM mit weniger Parametern (z. B. OPT-125M)

Spekulativ Und kontrastiv Die Dekodierung nutzt große und kleine LLMs, um eine zuverlässige und effiziente Textgenerierung zu erreichen.

Kontrastive Dekodierung ist eine Strategie, die die Tatsache ausnutzt, dass Fehler in großen LLMs (wie Wiederholungen, Inkohärenz) in kleinen LLMs noch ausgeprägter sind. Somit optimiert diese Strategie für die Token mit der höchsten Wahrscheinlichkeitsdifferenz zwischen dem kleinen und dem großen Modell.

Für eine einzelne Vorhersage generiert die kontrastive Dekodierung zwei Wahrscheinlichkeitsverteilungen:

• q = Logit-Wahrscheinlichkeiten für Amateurmodelle
• p = Logit-Wahrscheinlichkeiten für Expertenmodell

Der nächste Token wird anhand der folgenden Kriterien ausgewählt:

• Verwerfen Sie alle Token, die nach dem Expertenmodell keine ausreichend hohe Wahrscheinlichkeit haben (verwerfen p(x) < Alpha * max(p))
• Wählen Sie aus den verbleibenden Token dasjenige aus, das den größten Unterschied zwischen den Log-Wahrscheinlichkeiten des großen Modells und des kleinen Modells aufweist. max(p(x) – q(x)).

Implementierung der kontrastiven Dekodierung

from transformers import AutoTokenizer, AutoModelForCausalLM
import torch
# Load fashions and tokenizer
tokenizer = AutoTokenizer.from_pretrained('gpt2')
amateur_lm = AutoModelForCausalLM.from_pretrained('gpt2')
expert_lm = AutoModelForCausalLM.from_pretrained('gpt2-large')
def contrastive_decoding(immediate, max_length=50):
input_ids = tokenizer(immediate, return_tensors="pt").input_ids
whereas input_ids.form(1) < max_length:
# Generate newbie mannequin output
amateur_outputs = amateur_lm(input_ids, return_dict=True)
amateur_logits = torch.softmax(amateur_outputs.logits(:, -1, :), dim=-1)
log_probs_amateur = torch.log(amateur_logits)
# Generate knowledgeable mannequin output
expert_outputs = expert_lm(input_ids, return_dict=True)
expert_logits = torch.softmax(expert_outputs.logits(:, -1, :), dim=-1)
log_probs_exp = torch.log(expert_logits)
log_probs_diff = log_probs_exp - log_probs_amateur
# Set an alpha threshold to get rid of much less assured tokens in knowledgeable
alpha = 0.1
candidate_exp_prob = torch.max(expert_logits)
# Masks tokens beneath threshold for knowledgeable mannequin
V_head = expert_logits < alpha * candidate_exp_prob
# Choose the subsequent token from the log-probabilities distinction, ignoring masked values
token = torch.argmax(log_probs_diff.masked_fill(V_head, -torch.inf)).unsqueeze(0)
# Append token and accumulate generated textual content
input_ids = torch.cat((input_ids, token.unsqueeze(1)), dim=-1)
return tokenizer.batch_decode(input_ids)
immediate = "Giant Language Fashions are"
generated_text = contrastive_decoding(immediate, max_length=25)
print(generated_text)

Spekulative Dekodierung basiert auf dem Prinzip, dass das kleinere Modell aus derselben Verteilung wie das größere Modell Stichproben ziehen muss. Daher zielt diese Strategie darauf ab, so viele Vorhersagen wie möglich vom kleineren Modell zu akzeptieren, sofern sie mit der Verteilung des größeren Modells übereinstimmen.

Das kleinere Modell generiert N Spielsteine ​​nacheinander, als mögliche Vermutungen. Allerdings alle N Sequenzen werden als einzelner Batch in das größere Expertenmodell eingespeist, was schneller ist als die sequentielle Generierung.

Dies führt zu einem Cache für jedes Modell mit N Wahrscheinlichkeitsverteilungen in jedem Cache.

• q = Logit-Wahrscheinlichkeiten für Amateurmodelle
• p = Logit-Wahrscheinlichkeiten für Expertenmodell

Als nächstes werden die abgetasteten Token des Amateurmodells basierend auf den folgenden Bedingungen akzeptiert oder abgelehnt:

• Wenn die Wahrscheinlichkeit des Tokens in der Expertenverteilung (p) höher ist als in der Amateurverteilung (q), oder p(x) > q(x), Token akzeptieren
• Wenn die Wahrscheinlichkeit eines Tokens in der Expertenverteilung (p) niedriger ist als in der Amateurverteilung (q), oder p(x) < q(x)Token mit Wahrscheinlichkeit ablehnen 1 – p(x) / q(x)

Wenn ein Token abgelehnt wird, wird der nächste Token aus der Expertenverteilung oder der angepassten Verteilung entnommen. Darüber hinaus wird beim Novice- und Expertenmodell der Cache zurückgesetzt und neu generiert N Vermutungen und Wahrscheinlichkeitsverteilungen P Und Q.

Spekulative Dekodierung implementieren

from transformers import AutoTokenizer, AutoModelForCausalLM
import torch
# Load fashions and tokenizer
tokenizer = AutoTokenizer.from_pretrained('gpt2')
amateur_lm = AutoModelForCausalLM.from_pretrained('gpt2')
expert_lm = AutoModelForCausalLM.from_pretrained('gpt2-large')
# Pattern subsequent token from output distribution
def sample_from_distribution(logits):
sampled_index = torch.multinomial(logits, 1)
return sampled_index
def generate_cache(input_ids, n_tokens):
# Retailer logits at every step for newbie and knowledgeable fashions
amateur_logits_per_step = ()
generated_tokens = ()
batch_input_ids = ()
with torch.no_grad():
for _ in vary(n_tokens):
# Generate newbie mannequin output
amateur_outputs = amateur_lm(input_ids, return_dict=True)
amateur_logits = torch.softmax(amateur_outputs.logits(:, -1, :), dim=-1)
amateur_logits_per_step.append(amateur_logits)
# Sampling from newbie logits
next_token = sample_from_distribution(amateur_logits)
generated_tokens.append(next_token)
# Append to input_ids for subsequent era step
input_ids = torch.cat((input_ids, next_token), dim=-1)
batch_input_ids.append(input_ids.squeeze(0))
# Feed IDs to knowledgeable mannequin as batch 
batched_input_ids = torch.nn.utils.rnn.pad_sequence(batch_input_ids, batch_first=True, padding_value=0 )
expert_outputs = expert_lm(batched_input_ids, return_dict=True)
expert_logits = torch.softmax(expert_outputs.logits(:, -1, :), dim=-1)
return amateur_logits_per_step, expert_logits, torch.cat(generated_tokens, dim=-1)
def speculative_decoding(immediate, n_tokens=5, max_length=50):
input_ids = tokenizer(immediate, return_tensors="pt").input_ids
whereas input_ids.form(1) < max_length:
amateur_logits_per_step, expert_logits, generated_ids = generate_cache(
input_ids, n_tokens
)
accepted = 0
for n in vary(n_tokens):
token = generated_ids(:, n)(0)
r = torch.rand(1).merchandise()
# Extract chances
p_x = expert_logits(n)(token).merchandise()
q_x = amateur_logits_per_step(n)(0)(token).merchandise()
# Speculative decoding acceptance criterion
if ((q_x > p_x) and (r > (1 - p_x / q_x))):
break  # Reject token and restart the loop
else:
accepted += 1
# Test size
if (input_ids.form(1) + accepted) >= max_length:
return tokenizer.batch_decode(input_ids)
input_ids = torch.cat((input_ids, generated_ids(:, :accepted)), dim=-1)
if accepted < n_tokens:
diff = expert_logits(accepted) - amateur_logits_per_step(accepted)(0)
clipped_diff = torch.clamp(diff, min=0) 
# Pattern a token from the adjusted knowledgeable distribution
normalized_result = clipped_diff / torch.sum(clipped_diff, dim=0, keepdim=True)
next_token = sample_from_distribution(normalized_result)
input_ids = torch.cat((input_ids, next_token.unsqueeze(1)), dim=-1)
else:
# Pattern instantly from the knowledgeable logits for the final accepted token
next_token = sample_from_distribution(expert_logits(-1))
input_ids = torch.cat((input_ids, next_token.unsqueeze(1)), dim=-1)
return tokenizer.batch_decode(input_ids)
# Instance utilization
immediate = "Giant Language fashions are"
generated_text = speculative_decoding(immediate, n_tokens=3, max_length=25)
print(generated_text)

Auswertung

Wir können beide Dekodierungsansätze bewerten, indem wir sie mit einer naiven Dekodierungsmethode vergleichen, bei der wir zufällig das nächste Token aus der Wahrscheinlichkeitsverteilung auswählen.

def sequential_sampling(immediate, max_length=50):
"""
Carry out sequential sampling with the given mannequin.
"""
# Tokenize the enter immediate
input_ids = tokenizer(immediate, return_tensors="pt").input_ids
with torch.no_grad():
whereas input_ids.form(1) < max_length:
# Pattern from the mannequin output logits for the final token
outputs = expert_lm(input_ids, return_dict=True)
logits = outputs.logits(:, -1, :)
chances = torch.softmax(logits, dim=-1)
next_token = torch.multinomial(chances, num_samples=1)
input_ids = torch.cat((input_ids, next_token), dim=-1)
return tokenizer.batch_decode(input_ids)

Um die kontrastive Dekodierung zu bewerten, können wir die folgenden Metriken für den lexikalischen Reichtum verwenden.

• n-Gramm-Entropie: Misst die Unvorhersehbarkeit oder Vielfalt von N-Grammen im generierten Textual content. Eine hohe Entropie weist auf einen abwechslungsreicheren Textual content hin, während eine niedrige Entropie auf Wiederholung oder Vorhersagbarkeit hindeutet.
• eindeutig-n: Misst den Anteil eindeutiger N-Gramme im generierten Textual content. Höhere Distinct-n-Werte weisen auf eine größere lexikalische Vielfalt hin.

from collections import Counter
import math
def ngram_entropy(textual content, n):
"""
Compute n-gram entropy for a given textual content.
"""
# Tokenize the textual content
tokens = textual content.cut up()
if len(tokens) < n:
return 0.0  # Not sufficient tokens to kind n-grams
# Create n-grams
ngrams = (tuple(tokens(i:i + n)) for i in vary(len(tokens) - n + 1))
# Depend frequencies of n-grams
ngram_counts = Counter(ngrams)
total_ngrams = sum(ngram_counts.values())
# Compute entropy
entropy = -sum((rely / total_ngrams) * math.log2(rely / total_ngrams)
for rely in ngram_counts.values())
return entropy
def distinct_n(textual content, n):
"""
Compute distinct-n metric for a given textual content.
"""
# Tokenize the textual content
tokens = textual content.cut up()
if len(tokens) < n:
return 0.0  # Not sufficient tokens to kind n-grams
# Create n-grams
ngrams = (tuple(tokens(i:i + n)) for i in vary(len(tokens) - n + 1))
# Depend distinctive and whole n-grams
unique_ngrams = set(ngrams)
total_ngrams = len(ngrams)
return len(unique_ngrams) / total_ngrams if total_ngrams > 0 else 0.0
prompts = (
"Giant Language fashions are",
"Barack Obama was",
"Decoding technique is essential as a result of",
"A very good recipe for Halloween is",
"Stanford is understood for"
)
# Initialize accumulators for metrics
naive_entropy_totals = (0, 0, 0)  # For n=1, 2, 3
naive_distinct_totals = (0, 0)    # For n=1, 2
contrastive_entropy_totals = (0, 0, 0)
contrastive_distinct_totals = (0, 0)
for immediate in prompts:
naive_generated_text = sequential_sampling(immediate, max_length=50)(0)
for n in vary(1, 4):
naive_entropy_totals(n - 1) += ngram_entropy(naive_generated_text, n)
for n in vary(1, 3):
naive_distinct_totals(n - 1) += distinct_n(naive_generated_text, n)
contrastive_generated_text = contrastive_decoding(immediate, max_length=50)(0)
for n in vary(1, 4):
contrastive_entropy_totals(n - 1) += ngram_entropy(contrastive_generated_text, n)
for n in vary(1, 3):
contrastive_distinct_totals(n - 1) += distinct_n(contrastive_generated_text, n)
# Compute averages
naive_entropy_averages = (whole / len(prompts) for whole in naive_entropy_totals)
naive_distinct_averages = (whole / len(prompts) for whole in naive_distinct_totals)
contrastive_entropy_averages = (whole / len(prompts) for whole in contrastive_entropy_totals)
contrastive_distinct_averages = (whole / len(prompts) for whole in contrastive_distinct_totals)
# Show outcomes
print("Naive Sampling:")
for n in vary(1, 4):
print(f"Common Entropy (n={n}): {naive_entropy_averages(n - 1)}")
for n in vary(1, 3):
print(f"Common Distinct-{n}: {naive_distinct_averages(n - 1)}")
print("nContrastive Decoding:")
for n in vary(1, 4):
print(f"Common Entropy (n={n}): {contrastive_entropy_averages(n - 1)}")
for n in vary(1, 3):
print(f"Common Distinct-{n}: {contrastive_distinct_averages(n - 1)}")

Die folgenden Ergebnisse zeigen uns, dass die kontrastive Dekodierung die naive Stichprobenerhebung für diese Metriken übertrifft.

Naive Probenahme:
Durchschnittliche Entropie (n=1): 4,990499826537679
Durchschnittliche Entropie (n=2): 5,174765791328267
Durchschnittliche Entropie (n=3): 5,14373124004409
Durchschnittlicher Distinct-1: 0,8949694135740648
Durchschnittlicher Distinct-2: 0,9951219512195122

Kontrastive Dekodierung:
Durchschnittliche Entropie (n=1): 5,182773920916605
Durchschnittliche Entropie (n=2): 5,3495681172235665
Durchschnittliche Entropie (n=3): 5,313720275712986
Durchschnittlicher Distinct-1: 0,9028425204970866
Durchschnittlicher Distinct-2: 1,0

Um die spekulative Dekodierung zu bewerten, können wir uns die durchschnittliche Laufzeit für eine Reihe von Eingabeaufforderungen für verschiedene Arten ansehen N Werte.

import time
import matplotlib.pyplot as plt
# Parameters
n_tokens = vary(1, 11)
speculative_decoding_times = ()
naive_decoding_times = ()
prompts = (
"Giant Language fashions are",
"Barack Obama was",
"Decoding technique is essential as a result of",
"A very good recipe for Halloween is",
"Stanford is understood for"
)
# Loop by n_tokens values
for n in n_tokens:
avg_time_naive, avg_time_speculative = 0, 0
for immediate in prompts:
start_time = time.time()
_ = sequential_sampling(immediate, max_length=25)
avg_time_naive += (time.time() - start_time)
start_time = time.time()
_ = speculative_decoding(immediate, n_tokens=n, max_length=25)
avg_time_speculative += (time.time() - start_time)
naive_decoding_times.append(avg_time_naive / len(prompts))
speculative_decoding_times.append(avg_time_speculative / len(prompts))
avg_time_naive = sum(naive_decoding_times) / len(naive_decoding_times)
# Plotting the outcomes
plt.determine(figsize=(8, 6))
plt.bar(n_tokens, speculative_decoding_times, width=0.6, label='Speculative Decoding Time', alpha=0.7)
plt.axhline(y=avg_time_naive, shade='pink', linestyle='--', label='Naive Decoding Time')
# Labels and title
plt.xlabel('n_tokens', fontsize=12)
plt.ylabel('Common Time (s)', fontsize=12)
plt.title('Speculative Decoding Runtime vs n_tokens', fontsize=14)
plt.legend()
plt.grid(axis='y', linestyle='--', alpha=0.7)
# Present the plot
plt.present()
plt.savefig("plot.png")

Wir können sehen, dass die durchschnittliche Laufzeit für die naive Decodierung viel höher ist als für die spekulative Decodierung über N Werte.

Durch die Kombination großer und kleiner Sprachmodelle zur Dekodierung wird ein Gleichgewicht zwischen Qualität und Effizienz erreicht. Während diese Ansätze zusätzliche Komplexität beim Systemdesign und der Ressourcenverwaltung mit sich bringen, gelten ihre Vorteile auch für Konversations-KI, Echtzeitübersetzung und Inhaltserstellung.

Diese Ansätze erfordern eine sorgfältige Berücksichtigung der Bereitstellungsbeschränkungen. Beispielsweise können die zusätzlichen Speicher- und Rechenanforderungen beim Ausführen von Dualmodellen die Durchführbarkeit auf Edge-Geräten einschränken, obwohl dies durch Techniken wie Modellquantisierung gemildert werden kann.

Sofern nicht anders angegeben, stammen alle Bilder vom Autor.