Der Fortschritt generativer Modelle des maschinellen Lernens macht Pc zu kreativem Arbeiten befähigt. Im Bereich des Zeichnens von Bildern gibt es einige bemerkenswerte Modelle, mit denen Sie eine Textbeschreibung in eine Pixelanordnung umwandeln können. Die leistungsstärksten Modelle gehören heute zur Familie der Diffusionsmodelle. In diesem Beitrag erfahren Sie, wie ein solches Modell funktioniert und wie Sie seine Ausgabe steuern können.
Lass uns anfangen.

Kurze Einführung in Diffusionsmodelle zur Bilderzeugung
Foto von Dhruvin Pandya. Einige Rechte vorbehalten.
Überblick
Dieser Beitrag besteht aus drei Teilen; sie sind:
- Arbeitsablauf von Diffusionsmodellen
- Variation in der Ausgabe
- Wie es trainiert wurde
Arbeitsablauf von Diffusionsmodellen
In Anbetracht des Ziels, eine Beschreibung eines Bildes in Textform in ein Bild in einem Array von Pixeln umzuwandeln, sollte die Ausgabe des maschinellen Lernmodells ein Array von RGB-Werten sein. Aber wie soll man einem Modell Texteingaben bereitstellen und wie erfolgt die Konvertierung?
Da die Texteingabe die Ausgabe beschreibt, muss das Modell dies tun verstehen was der Textual content bedeutet. Je besser eine solche Beschreibung verstanden wird, desto genauer kann Ihr Modell die Ausgabe generieren. Daher funktioniert die triviale Lösung, den Textual content als Zeichenfolge zu behandeln, nicht intestine. Sie benötigen ein Modul, das natürliche Sprache verstehen kann, und die modernste Lösung wäre, die Eingabe als Einbettungsvektoren darzustellen.
Durch das Einbetten der Darstellung des Eingabetextes können Sie nicht nur den Textual content destillieren Bedeutung des Textes, sondern sorgt auch für eine einheitliche Kind der Eingabe, da der Textual content unterschiedlicher Länge in eine Standardgröße von Tensoren umgewandelt werden kann.
Es gibt mehrere Möglichkeiten, einen Tensor der Einbettungsdarstellung in Pixel umzuwandeln. Erinnern Sie sich daran, wie das Generative Adversarial Community (GAN) funktioniert; Sie sollten beachten, dass dies eine ähnliche Struktur aufweist, nämlich dass die Eingabe (Textual content) in eine latente Struktur (Einbettung) und dann in die Ausgabe (Pixel) umgewandelt wird.
Diffusionsmodelle sind eine Familie neuronaler Netzwerkmodelle, die die Einbettung als a betrachten Hinweis um ein Bild aus zufälligen Pixeln wiederherzustellen. Unten ist eine Abbildung aus der Arbeit von Rombach et al. Um diesen Arbeitsablauf zu veranschaulichen:
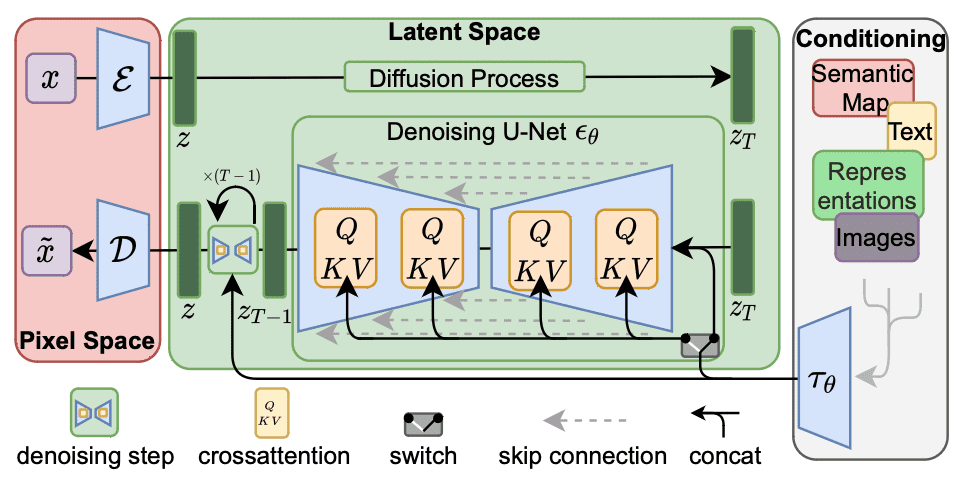
Stabile Diffusionsarchitektur. Abbildung von Rombach et al. (2021)
In dieser Abbildung erfolgt der Arbeitsablauf von rechts nach hyperlinks. Die Ausgabe hyperlinks besteht darin, einen Tensor mithilfe von a in einen Pixelraum umzuwandeln Decoder Netzwerk mit der Bezeichnung $mathcal{D}$. Die Eingabe rechts wird in ein eingebettetes $tau_theta$ umgewandelt, das als verwendet wird Konditionierungstensor. Die Schlüsselstruktur liegt im latenten Raum in der Mitte. Der Generierungsteil befindet sich in der unteren Hälfte des grünen Kastens, der $z_T$ mithilfe von a in $z_{T-1}$ umwandelt Rauschunterdrückungsnetzwerk $epsilon_theta$.
Das Entrauschungsnetzwerk nimmt einen Eingabetensor $z_T$ und die Einbettung $tau_theta$ und gibt einen Tensor $z_{T-1}$ aus. Die Ausgabe ist ein Tensor, der in dem Sinne „besser“ als die Eingabe ist, dass er besser zur Einbettung passt. In seiner einfachsten Kind tut der Decoder $mathcal{D}$ nichts anderes, als die Ausgabe aus dem latenten Raum zu kopieren. Die Eingabe- und Ausgabetensoren $z_T$ und $z_{T-1}$ des Entrauschungsnetzwerks sind Arrays von RGB-Pixeln, die das Netzwerk daraus erstellt Weniger laut.
Es wird Rauschunterdrückungsnetzwerk genannt, weil es davon ausgeht, dass die Einbettung die Ausgabe perfekt beschreiben kann, sich Eingabe und Ausgabe jedoch unterscheiden, weil einige Pixel durch Zufallswerte ersetzt werden. Das Netzwerkmodell zielte darauf ab, solche Zufallswerte zu entfernen und das ursprüngliche Pixel wiederherzustellen. Es ist eine schwierige Aufgabe, aber das Modell geht davon aus, dass die Rauschpixel gleichmäßig hinzugefügt werden und das Rauschen einem Gaußschen Modell folgt. Daher kann das Modell viele Male wiederverwendet werden, was jeweils zu einer Verbesserung der Eingabe führt. Unten finden Sie eine Abbildung aus dem Artikel von Ho et al. für ein solches Konzept:
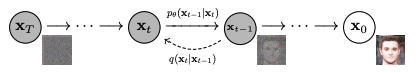
Ein Bild entrauschen. Abbildung von Ho et al. (2020)
Aufgrund dieser Struktur geht das Entrauschungsnetzwerk davon aus, dass die Eingabe $z_T$ und die Ausgabe $z_{T-1}$ die gleiche Kind haben, sodass das Netzwerk wiederholt werden kann, bis die endgültige Ausgabe $z$ erzeugt wird. Der entrauschende U-Internet-Block in der vorherigen Abbildung dient dazu, die Eingabe und Ausgabe in derselben Kind zu halten. Der Rauschunterdrückungsblock soll konzeptionell Folgendes ausführen:
$$
start{ausgerichtet}
w_t &= textrm{NoisePredictor}(z_t, tau_theta, t)
z_{t-1} &= z_t – w_t
finish{aligned}
$$
Das heißt, die Rauschkomponente $w_t$ wird aus dem verrauschten Bild $z_t$, dem Konditionierungstensor $tau_theta$ und der Schrittzahl $t$ vorhergesagt. Der Rauschprädiktor basiert dann auf $t$, um den Rauschpegel in $z_t$ zu schätzen, abhängig davon, wie das endgültige Bild $z=z_0$ aussehen sollte, wie durch den Tensor $tau_theta$ beschrieben. Der Wert von $t$ ist für den Prädiktor hilfreich, denn je größer der Wert, desto stärker ist das Rauschen in $z_t$.
Durch Subtrahieren des Rauschens von $z_t$ erhält man das entrauschte Bild $z_{t-1}$, das erneut in das Entrauschungsnetzwerk eingespeist werden kann, bis $z=z_0$ erzeugt wird. Die Häufigkeit, mit der $T$ dieses Netzwerk den Tensor verarbeitet, ist ein Entwurfsparameter für das gesamte Diffusionsmodell. Da in diesem Modell das Rauschen als Gaußsches Rauschen formuliert ist, besteht ein Teil des Decoders $mathcal{D}$ darin, den latenten Raumtensor $z$ in einen Dreikanaltensor umzuwandeln und Gleitkommawerte in RGB zu quantisieren.
Variation in der Ausgabe
Sobald das neuronale Netzwerk trainiert ist, sind die Gewichte in jeder Schicht festgelegt und die Ausgabe ist deterministisch, solange die Eingabe deterministisch ist. In diesem Diffusionsmodell-Workflow ist die Eingabe jedoch der Textual content, der in Einbettungsvektoren umgewandelt wird. Das Entrauschungsmodell benötigt eine zusätzliche Eingabe, den anfänglichen $z_T$-Tensor im latenten Raum. Dies wird normalerweise zufällig generiert, beispielsweise durch Abtasten einer Gaußschen Verteilung und Ausfüllen des Tensors der Kind, die das Entrauschungsnetzwerk erwartet. Mit einem anderen Starttensor erhalten Sie eine andere Ausgabe. Auf diese Weise können Sie mit demselben Eingabetext unterschiedliche Ausgaben generieren.
Tatsächlich ist die Realität viel komplizierter. Denken Sie daran, dass das Entrauschungsnetzwerk in mehreren Schritten ausgeführt wird, wobei jeder Schritt darauf abzielt, die Ausgabe ein wenig zu verbessern, bis die makellose Endausgabe erzeugt wird. Das Netzwerk kann einen zusätzlichen Hinweis darauf erhalten, in welchem Schritt es sich befindet (z. B. Schritt 5 von insgesamt 10 geplanten Schritten). Gaußsches Rauschen wird durch seinen Mittelwert und seine Variation parametrisiert, für deren Berechnung Sie eine Funktion bereitstellen können. Je besser Sie das bei jedem Schritt erwartete Rauschen modellieren können, desto besser kann das Entrauschungsnetzwerk das Rauschen entfernen. Im Stabile Verbreitung Modell benötigt das Entrauschungsnetzwerk eine Probe zufälligen Rauschens, die die Rauschintensität widerspiegelt, wie in diesem Schritt, um die Rauschkomponente aus einem verrauschten Bild vorherzusagen. Algorithmus 2 in der Abbildung unten zeigt dies, wobei eine solche Zufälligkeit als $sigma_tmathbf{z}$ eingeführt wird. Sie können die auswählen Sampler für einen solchen Zweck. Einige Sampler konvergieren schneller als andere (dh Sie verwenden weniger Schritte). Sie können das Latentraummodell auch als betrachten Variations-Autoencoderbei dem sich die eingeführten Variationen auch auf die Ausgabe auswirken.
Wie es trainiert wurde
Am Beispiel des Secure Diffusion-Modells können Sie sehen, dass die wichtigste Komponente im Arbeitsablauf das Denosierungsmodell im latenten Raum ist. Tatsächlich wird das Eingabemodell nicht trainiert, sondern übernimmt ein vorhandenes Texteinbettungsmodell wie BERT oder T5. Das Ausgabemodell kann auch ein Standardmodell sein, beispielsweise ein hochauflösendes Modell, das ein 256×256-Pixel-Bild in ein 512×512-Pixel-Bild umwandelt.
Das Coaching des Netzwerkmodells zur Rauschunterdrückung läuft konzeptionell wie folgt ab: Sie wählen ein Bild aus und fügen etwas Rauschen hinzu. Dann haben Sie ein Tupel aus drei Komponenten erstellt: dem Bild, dem Rauschen und dem verrauschten Bild. Anschließend wird das Netzwerk darauf trainiert, den Rauschanteil des verrauschten Bildes abzuschätzen. Der Rauschanteil kann durch unterschiedliche Gewichtung des Rauschens zu den Pixeln sowie durch die Gaußschen Parameter zur Erzeugung des Rauschens variieren. Der Trainingsalgorithmus wird in Algorithmus 1 wie folgt dargestellt:

Trainings- und Sampling-Algorithmen. Abbildung von Ho et al. (2020)
Da das Entrauschungsnetzwerk davon ausgeht, dass das Rauschen vorhanden ist Zusatzstoff, kann das vorhergesagte Rauschen von der Eingabe subtrahiert werden, um die Ausgabe zu erzeugen. Wie oben beschrieben, verwendet das Entrauschungsnetzwerk nicht nur das Bild als Eingabe, sondern auch die Einbettung, die die Texteingabe widerspiegelt. Die Einbettung spielt insofern eine Rolle, als das zu erkennende Rauschen an die Einbettung gebunden ist, was bedeutet, dass die Ausgabe sich auf die Einbettung beziehen sollte und das zu erkennende Rauschen einer bedingten Wahrscheinlichkeitsverteilung entsprechen sollte. Technisch gesehen treffen das Bild und die Einbettung über einen Kreuzaufmerksamkeitsmechanismus im latenten Modell aufeinander, der im obigen Algorithmengerüst nicht dargestellt ist.
Es gibt viel Vokabular, um ein Bild zu beschreiben, und Sie können sich vorstellen, dass es nicht einfach ist, dem Netzwerkmodell beizubringen, wie man ein Wort einem Bild zuordnet. Es wird berichtet, dass das Secure Diffusion-Modell beispielsweise mit 2,3 Milliarden Bildern trainiert wurde und 150.000 GPU-Stunden verbrauchte LAION-5B-Datensatz (mit 5,85 Milliarden Bildern mit Textbeschreibungen). Sobald das Modell jedoch trainiert ist, können Sie es auf einem Standardcomputer wie Ihrem Laptop computer verwenden.
Weitere Lektüre
Nachfolgend finden Sie mehrere Veröffentlichungen, die die Diffusionsmodelle für die Bilderzeugung, wie wir sie heute kennen, erstellt haben:
- „Hochauflösende Bildsynthese mit latenten Diffusionsmodellen“ von Rombach, Blattmann, Lorenz, Esser und Ommer (2021)
arXiv 2112.10752 - „Diffusionsprobabilistische Modelle entrauschen“ von Ho, Jain und Abbeel (2020)
arXiv 2006.11239 - „Diffusionsmodelle schlagen GANs bei der Bildsynthese“ von Dhariwal und Nichol (2021)
arXiv 2105.05233 - „Improved Denoising Diffusion Probabilistic Fashions“ von Nichol und Dhariwal (2021)
arXiv 2102.09672
Zusammenfassung
In diesem Beitrag haben Sie einen Überblick über die Funktionsweise eines Diffusionsmodells erhalten. Insbesondere haben Sie gelernt
- Der Bilderzeugungs-Workflow besteht aus mehreren Schritten, das Diffusionsmodell arbeitet im latenten Raum als entrauschendes neuronales Netzwerk.
- Die Bilderzeugung erfolgt ausgehend von einem verrauschten Bild, bei dem es sich um eine Anordnung zufällig generierter Pixel handelt.
- Bei jedem Schritt im latenten Raum entfernt das Entrauschungsnetzwerk etwas Rauschen, abhängig von der Eingabetextbeschreibung des endgültigen Bildes in Kind von Einbettungsvektoren.
- Das Ausgabebild wird durch Dekodierung der Ausgabe aus dem latenten Raum erhalten.
