Teil 3 unseres Tutorials zum Thema Gaussian Splatting zeigt, wie man Splats auf ein 2D-Bild rendert.
Schließlich erreichen wir die spannendste Part des Gaussian Splatting-Prozesses: das Rendern! Dieser Schritt ist wohl der wichtigste, da er den Realismus unseres Modells bestimmt. Er ist aber vielleicht auch der einfachste. In Teil 1 Und Teil 2 unserer Serie haben wir gezeigt, wie man Roh-Splats in ein renderfähiges Format umwandelt, aber jetzt müssen wir die Arbeit tatsächlich selbst erledigen und auf einen festen Satz von Pixeln rendern. Die Autoren haben eine schnelle Rendering-Engine mit CUDA entwickelt, die etwas schwierig zu verstehen sein kann. Daher halte ich es für sinnvoll, den Code zunächst in Python durchzugehen und der Übersichtlichkeit halber einfache for-Schleifen zu verwenden. Für diejenigen, die tiefer eintauchen möchten, ist der gesamte erforderliche Code auf unserer G verfügbar.itHub.
Lassen Sie uns besprechen, wie jedes einzelne Pixel gerendert wird. Aus unserer vorherigen Artikelhaben wir alle notwendigen Komponenten: 2D-Punkte, zugehörige Farben, Kovarianz, sortierte Tiefenreihenfolge, inverse Kovarianz in 2D, minimale und maximale x- und y-Werte für jeden Splat und zugehörige Opazität. Mit diesen Komponenten können wir jedes Pixel rendern. Bei gegebenen spezifischen Pixelkoordinaten iterieren wir durch alle Splats, bis wir einen Sättigungsschwellenwert erreichen, und folgen dabei der Splat-Tiefenreihenfolge relativ zur Kameraebene (auf die Kameraebene projiziert und dann nach Tiefe sortiert). Für jeden Splat prüfen wir zunächst, ob die Pixelkoordinate innerhalb der durch die minimalen und maximalen x- und y-Werte definierten Grenzen liegt. Diese Prüfung legt fest, ob wir mit dem Rendern fortfahren oder den Splat für diese Koordinaten ignorieren sollen. Als Nächstes berechnen wir die Gaußsche Splat-Stärke an der Pixelkoordinate mithilfe des Splat-Mittelwerts, der Splat-Kovarianz und der Pixelkoordinaten.
def compute_gaussian_weight(
pixel_coord: torch.Tensor, # (1, 2) tensor
point_mean: torch.Tensor,
inverse_covariance: torch.Tensor,
) -> torch.Tensor:distinction = point_mean - pixel_coord
energy = -0.5 * distinction @ inverse_covariance @ distinction.T
return torch.exp(energy).merchandise()
Wir multiplizieren dieses Gewicht mit der Deckkraft des Splats, um einen Parameter namens Alpha zu erhalten. Bevor wir diesen neuen Wert zum Pixel hinzufügen, müssen wir prüfen, ob wir unseren Sättigungsschwellenwert überschritten haben. Wir möchten nicht, dass ein Splat hinter anderen Splats die Pixelfärbung beeinflusst und Rechenressourcen verbraucht, wenn das Pixel bereits gesättigt ist. Daher verwenden wir einen Schwellenwert, der es uns ermöglicht, das Rendering zu stoppen, sobald er überschritten wird. In der Praxis beginnen wir unseren Sättigungsschwellenwert bei 1 und multiplizieren ihn dann mit min(0,99, (1 – Alpha)), um einen neuen Wert zu erhalten. Wenn dieser Wert kleiner als unser Schwellenwert (0,0001) ist, stoppen wir das Rendering dieses Pixels und betrachten es als abgeschlossen. Wenn nicht, fügen wir die Farben gewichtet mit dem Wert Sättigung * (1 – Alpha) hinzu und aktualisieren die Sättigung als neue_Sättigung = alte_Sättigung * (1 – Alpha). Schließlich durchlaufen wir jedes Pixel (oder in der Praxis jede 16×16-Kachel) und rendern. Der vollständige Code ist unten dargestellt.
def render_pixel(
self,
pixel_coords: torch.Tensor,
points_in_tile_mean: torch.Tensor,
colours: torch.Tensor,
opacities: torch.Tensor,
inverse_covariance: torch.Tensor,
min_weight: float = 0.000001,
) -> torch.Tensor:
total_weight = torch.ones(1).to(points_in_tile_mean.machine)
pixel_color = torch.zeros((1, 1, 3)).to(points_in_tile_mean.machine)
for point_idx in vary(points_in_tile_mean.form(0)):
level = points_in_tile_mean(point_idx, :).view(1, 2)
weight = compute_gaussian_weight(
pixel_coord=pixel_coords,
point_mean=level,
inverse_covariance=inverse_covariance(point_idx),
)
alpha = weight * torch.sigmoid(opacities(point_idx))
test_weight = total_weight * (1 - alpha)
if test_weight < min_weight:
return pixel_color
pixel_color += total_weight * alpha * colours(point_idx)
total_weight = test_weight
# in case we by no means attain saturation
return pixel_color
Da wir nun ein Pixel rendern können, können wir auch einen Bildausschnitt rendern, oder was die Autoren als „Kachel“ bezeichnen!
def render_tile(
self,
x_min: int,
y_min: int,
points_in_tile_mean: torch.Tensor,
colours: torch.Tensor,
opacities: torch.Tensor,
inverse_covariance: torch.Tensor,
tile_size: int = 16,
) -> torch.Tensor:
"""Factors in tile must be organized so as of depth"""tile = torch.zeros((tile_size, tile_size, 3))
# iterate by tiles for extra environment friendly processing
for pixel_x in vary(x_min, x_min + tile_size):
for pixel_y in vary(y_min, y_min + tile_size):
tile(pixel_x % tile_size, pixel_y % tile_size) = self.render_pixel(
pixel_coords=torch.Tensor((pixel_x, pixel_y))
.view(1, 2)
.to(points_in_tile_mean.machine),
points_in_tile_mean=points_in_tile_mean,
colours=colours,
opacities=opacities,
inverse_covariance=inverse_covariance,
)
return tile
Und schließlich können wir alle diese Kacheln verwenden, um ein ganzes Bild zu rendern. Beachten Sie, wie wir überprüfen, ob der Splat tatsächlich die aktuelle Kachel beeinflusst (x_in_tile- und y_in_tile-Code).
def render_image(self, image_idx: int, tile_size: int = 16) -> torch.Tensor:
"""For every tile must verify if the purpose is within the tile"""
preprocessed_scene = self.preprocess(image_idx)
peak = self.photographs(image_idx).peak
width = self.photographs(image_idx).widthpicture = torch.zeros((width, peak, 3))
for x_min in tqdm(vary(0, width, tile_size)):
x_in_tile = (x_min >= preprocessed_scene.min_x) & (
x_min + tile_size <= preprocessed_scene.max_x
)
if x_in_tile.sum() == 0:
proceed
for y_min in vary(0, peak, tile_size):
y_in_tile = (y_min >= preprocessed_scene.min_y) & (
y_min + tile_size <= preprocessed_scene.max_y
)
points_in_tile = x_in_tile & y_in_tile
if points_in_tile.sum() == 0:
proceed
points_in_tile_mean = preprocessed_scene.factors(points_in_tile)
colors_in_tile = preprocessed_scene.colours(points_in_tile)
opacities_in_tile = preprocessed_scene.sigmoid_opacity(points_in_tile)
inverse_covariance_in_tile = preprocessed_scene.inverse_covariance_2d(
points_in_tile
)
picture(x_min : x_min + tile_size, y_min : y_min + tile_size) = (
self.render_tile(
x_min=x_min,
y_min=y_min,
points_in_tile_mean=points_in_tile_mean,
colours=colors_in_tile,
opacities=opacities_in_tile,
inverse_covariance=inverse_covariance_in_tile,
tile_size=tile_size,
)
)
return picture
Jetzt, da wir alle notwendigen Komponenten haben, können wir endlich ein Bild rendern. Wir nehmen alle 3D-Punkte aus dem Treehill-Datensatz und initialisieren sie als Gaußsche Splats. Um eine aufwändige Suche nach dem nächsten Nachbarn zu vermeiden, initialisieren wir alle Skalenvariablen als .01 (Beachten Sie, dass wir bei einer so kleinen Varianz eine starke Konzentration von Splats an einer Stelle benötigen, damit sie sichtbar sind. Eine größere Varianz macht den Prozess ziemlich langsam.). Dann müssen wir nur noch render_image mit der Bildnummer aufrufen, die wir emulieren möchten, und wie Sie sehen, erhalten wir einen spärlichen Satz von Punktwolken, die unserem Bild ähneln! (Sehen Sie sich unseren Bonusabschnitt unten an, um einen gleichwertigen CUDA-Kernel mit dem raffinierten Device von pyTorch zu finden, das CUDA-Code kompiliert!)
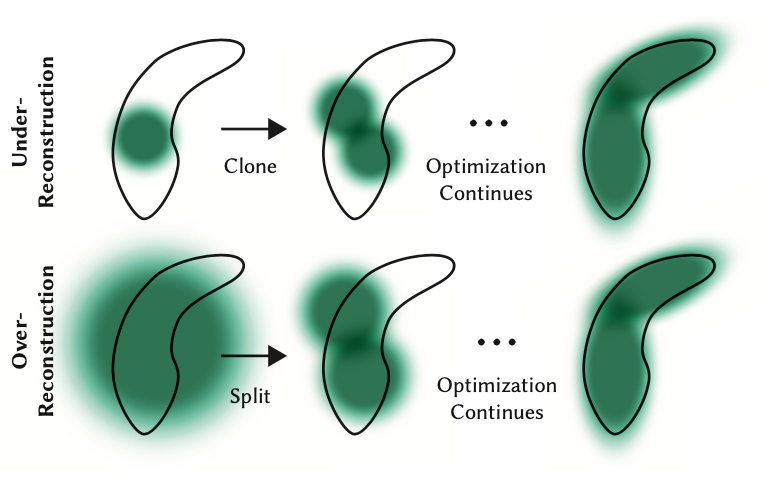
Obwohl der Rückwärtsdurchlauf nicht Teil dieses Tutorials ist, sollte angemerkt werden, dass wir, obwohl wir nur mit diesen wenigen Punkten beginnen, bald Hunderttausende von Splats für die meisten Szenen haben. Dies wird durch das Aufteilen großer Splats (definiert durch größere Varianz auf den Achsen) in kleinere Splats und das Entfernen von Splats mit extrem geringer Opazität verursacht. Wenn wir beispielsweise die Skala wirklich auf den Mittelwert der drei nächsten Nachbarn initialisieren würden, hätten wir einen Großteil des Raums abgedeckt. Um feine Particulars zu erhalten, müssten wir diese in viel kleinere Splats aufteilen, die feine Particulars erfassen können. Sie müssen auch Bereiche mit sehr wenigen Gaußschen Verteilungen füllen. Sie bezeichnen diese beiden Szenarien als Überrekonstruktion und Unterrekonstruktion und definieren beide Szenarien durch große Gradientenwerte für verschiedene Splats. Sie teilen oder klonen dann die Splats je nach Größe (siehe Bild unten) und setzen den Optimierungsprozess fort.
Obwohl der Rückwärtsdurchlauf in diesem Tutorial nicht behandelt wird, ist es wichtig zu beachten, dass wir mit nur wenigen Punkten beginnen, aber bald Hunderttausende von Splats in den meisten Szenen haben. Diese Zunahme ist auf die Aufteilung großer Splats (mit größeren Varianzen auf den Achsen) in kleinere und die Entfernung von Splats mit sehr geringer Opazität zurückzuführen. Wenn wir beispielsweise den Maßstab zunächst auf den Mittelwert der drei nächsten Nachbarn einstellen, wäre der größte Teil des Raums abgedeckt. Um feine Particulars zu erreichen, müssen wir diese großen Splats in viel kleinere aufteilen. Darüber hinaus müssen Bereiche mit sehr wenigen Gaußschen Verteilungen aufgefüllt werden. Diese Szenarien werden als Überrekonstruktion und Unterrekonstruktion bezeichnet und sind durch große Gradientenwerte für verschiedene Splats gekennzeichnet. Abhängig von ihrer Größe werden Splats aufgeteilt oder geklont (siehe Abbildung unten) und der Optimierungsprozess wird fortgesetzt.
Und das ist eine einfache Einführung in Gaussian Splatting! Sie sollten jetzt eine gute Vorstellung davon haben, was genau im Vorwärtsdurchgang eines Gaussian-Szenen-Renderings passiert. Das ist zwar ein wenig entmutigend und nicht gerade ein neuronales Netzwerk, aber alles, was man braucht, ist ein bisschen lineare Algebra und wir können 3D-Geometrie in 2D rendern!
Hinterlassen Sie gerne Kommentare zu verwirrenden Themen oder wenn ich etwas falsch gemacht habe. Sie können jederzeit über LinkedIn oder Twitter mit mir in Kontakt treten!