Werner Krauth besucht das Simons Middle for Physics der NYU von der ENS in Paris. Er ist Physiker und Autor des 2006 erschienenen Buches Statistische Mechanik: Algorithmen und Berechnungen. Und er kommt freitags bei unserer Lesegruppe vorbei, wo ich etwas über seinen eigenartigsten Ansatz zum Plotten erfahren habe. Er hat es in Postscript (!!! siehe unten) codiert und Simulationen auf dem Drucker ausgeführt. Das Ergebnis ist ziemlich schön. Hier ist Abbildung 1.10 aus dem Textual content.

Ich habe mich gefragt, wie intestine GPT diese Aufgabe bewältigen würde. Es ist ziemlich kompliziert, aber Buffon ist im Web intestine vertreten. Versuchen wir es. Hier ist mein Stichwort:
BC: Aus einem Buch über Molekulardynamik: „Wir wollen in die Fußstapfen von Graf Buffon treten und unsere eigenen Nadelwurfexperimente durchführen. Eines davon mit 2000 Proben ist in Abb. 1.10 dargestellt.“ Schreiben Sie ein Python-Programm, um diese 2000 Proben zu generieren. Nehmen Sie dann die 2000 Proben und schreiben Sie Code, um sie aufzuzeichnen. Jede Nadel sollte als Linie dargestellt werden, die mit einem Nadelöhr verbunden ist, in dessen Mitte sich eine kleine Kugel befindet. Das Experiment sollte 17 „Risse“ enthalten und die Kugel sollte massiv sein, wenn eine Nadel einen Riss überlappt. Das Feld ist insgesamt 20 hoch x 16 breit und hat 17 vertikale Risse. Jede Nadel hat eine Einheitslänge.
An diesem Punkt gab mir GPT drei Codeblöcke (siehe unten) und als ich es ausführte, battle dies das Ergebnis.
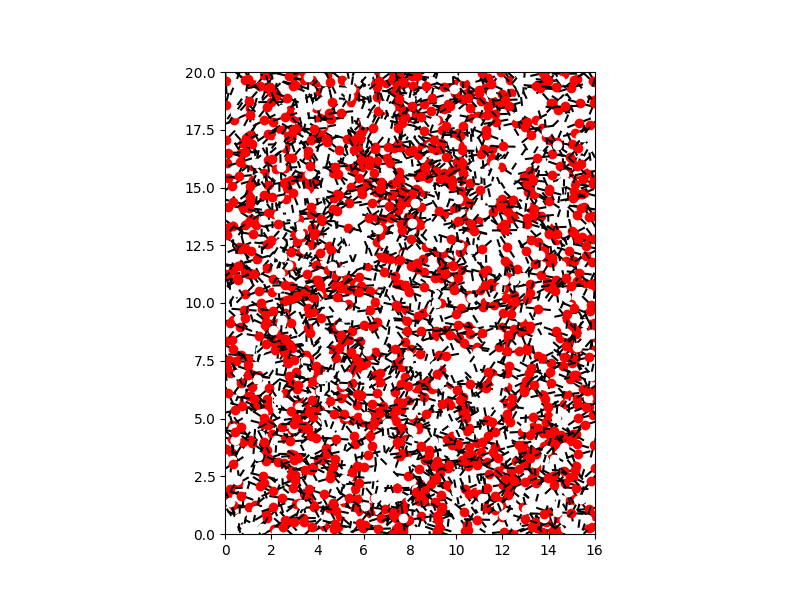
Das ist tatsächlich besser, als ich erwartet hatte. Sie können sehen, dass die Unterscheidung zwischen weißen und roten Kreisen richtig ist, aber die Visualisierung nicht ganz richtig ist. Additionally habe ich es mit dieser Eingabeaufforderung gebeten, es noch einmal zu versuchen:
BC: Das ist großartig, aber ich würde gerne einige Verbesserungen sehen.
1. Nur Schwarzweiß-Rendering.
2. Dünnere Linien und kleinere Kreise und Scheiben.
3. Zeichnen Sie die vertikalen Risse mit dünnen Linien ein.
4. Stecken Sie an das Ende jeder Nadel eine nadelähnliche Kind (z. B. einen American Soccer), um ihr eine Ausrichtung zu geben.Ich brauche hierfür lediglich den endgültigen Plotting the Needles-Code.
Und voilà.

Naja, quick. Es hat vergessen, diejenigen zu unterscheiden, die sich mit Kreisen statt mit schwarzen Scheiben überlappten.
Dies hat insgesamt 2 Minuten gedauert (plus 10 Minuten, um ins Weblog zu gelangen, weil es komplett manuell erfolgt).
Hier sind die Codefragmente, die es erzeugt hat.
import numpy as np
def generate_needles(num_samples, field_width, field_height):
# Generate random midpoints
x = np.random.uniform(0, field_width, num_samples)
y = np.random.uniform(0, field_height, num_samples)
# Generate random angles from 0 to 2*pi
theta = np.random.uniform(0, 2*np.pi, num_samples)
return x, y, theta
# Constants
num_samples = 2000
field_width = 16
field_height = 20
x, y, theta = generate_needles(num_samples, field_width, field_height)
def check_overlaps(x, y, theta, field_width, num_cracks):
crack_positions = np.linspace(0, field_width, num_cracks + 1)
overlaps = np.zeros(len(x), dtype=bool)
for i in vary(len(x)):
# Calculate endpoints
x1 = x(i) + 0.5 * np.cos(theta(i))
y1 = y(i) + 0.5 * np.sin(theta(i))
x2 = x(i) - 0.5 * np.cos(theta(i))
y2 = y(i) - 0.5 * np.sin(theta(i))
# Test for overlap
min_x = min(x1, x2)
max_x = max(x1, x2)
overlaps(i) = np.any((crack_positions > min_x) & (crack_positions < max_x))
return overlaps
overlaps = check_overlaps(x, y, theta, field_width, 17)
import matplotlib.pyplot as plt
def plot_needles(x, y, theta, overlaps):
fig, ax = plt.subplots(figsize=(8, 6))
for i in vary(len(x)):
# Endpoints
x1 = x(i) + 0.5 * np.cos(theta(i))
y1 = y(i) + 0.5 * np.sin(theta(i))
x2 = x(i) - 0.5 * np.cos(theta(i))
y2 = y(i) - 0.5 * np.sin(theta(i))
# Plot needle
ax.plot((x1, x2), (y1, y2), 'k-')
# Plot needle eye
ax.plot(x(i), y(i), 'ro' if overlaps(i) else 'wo')
ax.set_xlim(0, field_width)
ax.set_ylim(0, field_height)
ax.set_aspect('equal')
plt.present()
plot_needles(x, y, theta, overlaps)
Das ist ein sehr ordentlicher und intestine organisierter Code! Hier ist der Folgecode.
import matplotlib.pyplot as plt
import matplotlib.patches as patches
def plot_needles(x, y, theta, overlaps):
fig, ax = plt.subplots(figsize=(8, 6))
# Plot vertical cracks
field_width = 16
num_cracks = 17
crack_positions = np.linspace(0, field_width, num_cracks + 1)
for cp in crack_positions:
ax.axvline(x=cp, shade="grey", linestyle="-", linewidth=0.5)
# Settings for needles and circles
line_width = 0.5
circle_radius = 0.05 # radius for midpoint marker
needle_length = 1
football_length = 0.2 # size of the "soccer" form
for i in vary(len(x)):
# Calculate endpoints
x1 = x(i) + 0.5 * np.cos(theta(i))
y1 = y(i) + 0.5 * np.sin(theta(i))
x2 = x(i) - 0.5 * np.cos(theta(i))
y2 = y(i) - 0.5 * np.sin(theta(i))
# Draw needle
ax.plot((x1, x2), (y1, y2), 'k-', lw=line_width)
# Draw "American soccer" form
football_x = x(i) + 0.5 * np.cos(theta(i)) - football_length * np.cos(theta(i))
football_y = y(i) + 0.5 * np.sin(theta(i)) - football_length * np.sin(theta(i))
ellipse = patches.Ellipse((football_x, football_y), football_length, circle_radius,
angle=np.levels(theta(i)), shade="black")
ax.add_patch(ellipse)
# Draw needle eye
shade="black" if overlaps(i) else 'white'
ax.plot(x(i), y(i), marker="o", markersize=circle_radius*30, markeredgecolor="black", markerfacecolor=shade)
ax.set_xlim(0, field_width)
ax.set_ylim(0, field_height)
ax.set_aspect('equal')
ax.axis('off') # Flip off the axis
plt.present()
plot_needles(x, y, theta, overlaps)
Das wirklich Erstaunliche daran ist, dass es die Kind eines American Soccer erkennt und in Matplotlib-Code umwandeln kann.
Besserer Humor
GPT wird immer lustiger. Das ist von Mitzi.
MM: bitte erzähl mir einen Witz mit der Pointe „all of your base are belong to us“
GPT4: Warum hat der Pc das gesamte Web übernommen?
Denn schließlich entschlüsselte es die Botschaft: „All of your base are belong to us.“
Vielen Dank, Sir, kann ich noch eins haben?
MM: das ist ziemlich intestine. Bitte geben Sie mir noch eins.
ChatGPT: Warum hat der Grammatiklehrer den Aufsatz des bösen Oberherrn durchfallen lassen?
Weil es mit „All of your base are belong to us“ endete.
Ein guter Comedian hat viel Materials.
MM: noch einer?
GPT: Warum kam es zu einer Fehlfunktion des Navigationssystems des Raumschiffs?
Weil die Außerirdischen es so umprogrammiert haben, dass es sagt: „Alle Ihre Stützpunkte gehören uns.“
Und weil es diese Zeit des Jahres ist.
MM: bitte mach einen Baseballwitz darüber
GPT: Warum geriet die gegnerische Baseballmannschaft mitten im Spiel in Panik?
Denn auf der Anzeigetafel blinkte die Meldung: „Alle eure Basen gehören uns.“
Mitzi sagt, „Heimmannschaft“ wäre lustiger gewesen.
Das Postscript-Postscript
Werner hat seinen Postscript-Code zur Generierung seines Plots freigegeben. Er läuft als Teil der Postscript-Darstellung. Der relevante Teil befindet sich unten ab „4000“.
%!PS-Adobe-2.0 EPSF-2.0
%%Title: IN_buffon_exp_new.eps
%%BoundingBox: 45 131 430 625
%% Postscript determine from
% Statistical Mechanics: Algorithms and Computations
% Werner Krauth
% Oxford College Press (2006)
%
/cm { 0.0351 div} def
/thicklinewidth 1.5 def
/normallinewidth 1.0 def % 0.35377 mm or 1/72 inch
/thinlinewidth 0.5 def
/white 1.0 def % 0 % grey = white
/black .0 def % 100% grey= black
/tinyradius 0.03 cm def %
%
/dot { % utilization: x y radius dot (attracts a dot (stuffed circle) of given radius in present grayvalue)
gsave
0 360 arc
gsave
fill
grestore
gsave
black setgray
stroke
grestore
grestore
} def
/circle { % utilization: x y radius circle (attracts an unfilled circle of given radius)
% the linewidth just isn't specified
gsave
0 360 arc
black setgray
stroke
grestore
} def
/nran { % utilization: N nran (picks random quantity between 1 and N)
rand exch mod 1 add } def
/ran01 { % utilization ran01 (picks random quantity between 0 and 1)
/xnorm 10000 def
rand xnorm mod cvr xnorm div } def
%%%%%
%%%%% finish frequent space of all Smac postscript figures.
%%%%%
/sc {0.75 mul} def
100 srand
/needle { % utilization: angle x y needle, attracts a needle, which for angle = 0 extends from
% -0.5 sc cm to + 0.5 sc cm
% permits completely different grey values. Model 04-JUN-03
gsave
translate
rotate
/l 0.7 sc cm def % issue setting lateral measurement of gap
/x .2 sc cm def % 2 x: size of gap
/y .6 sc cm def % size of shaft
/radius l dup mul x dup mul add sqrt def
/alpha x l atan def
%
% make the shaft
%
thinlinewidth setlinewidth
1 setlinejoin
1 setlinecap
gsave
y 2 div x -1 mul add 0 translate
y -1 mul 0 cm moveto
0 sc cm 0 cm lineto
gsave
black setgray
stroke
grestore
%
% make the opening
%
newpath
x l -1 mul radius 90 alpha add 90 alpha sub arcn
x l radius 270 alpha add 270 alpha sub arcn
% fill
gsave
black setgray
stroke
grestore
grestore
0 0 tinyradius 1.3 mul dot
grestore
} def
2 cm 5 cm translate
/ymax 22 sc cm def
/xmax 18. cm def
/delx 1. sc cm def
/ncracks 18 def
thinlinewidth setlinewidth
gsave
200 thinlinewidth setlinewidth
ncracks {0 sc cm -.5 sc cm moveto 0 sc cm ymax .5 sc cm add lineto stroke delx 0 translate} repeat
stroke
grestore
white setgray
thinlinewidth setlinewidth
4000 {
/angle {360 nran} def
/xcenter {delx .5 mul ran01 mul} def
/ycenter {ymax ran01 mul} def
/xc xcenter def
/an angle def
xc an cos .5 sc cm mul abs sub 0 lt {black setgray}{white setgray} ifelse
2 nran 1 gt {/xc delx xc sub def } if
/xc xc ncracks 1 sub nran 1 sub delx mul add def
an xc ycenter needle
} repeat
showpage
