Wie würden Sie einen maschinellen Lernalgorithmus erstellen, um die folgenden Arten von Problemen zu lösen?
- Sagen Sie voraus, welche Athleten bei den Olympischen Spielen eine Medaille gewinnen werden.
- Sagen Sie voraus, wie ein Schuh an einem Fuß sitzen wird (zu klein, perfekt, zu groß).
- Sagen Sie voraus, wie viele Sterne ein Kritiker einem Movie geben wird.
Wenn Sie auf Ihr typisches Toolkit zurückgreifen, werden Sie wahrscheinlich entweder auf Regression oder Multiklassenklassifizierung zurückgreifen. Bei der Regression behandeln Sie vielleicht die Anzahl der Sterne (1-5) in der Frage des Filmkritikers als Ihr Ziel und trainieren ein Modell mit dem mittleren quadratischen Fehler als Verlustfunktion. Bei der Multiklassenklassifizierung behandeln Sie vielleicht Bronze-, Silber- und Goldmedaillen als drei separate Klassen und trainieren ein Modell mit Kreuzentropieverlust.
Während diese Ansätze dürfen Arbeit, ignorieren sie einen grundlegenden Aspekt der Vorhersageziele in den vorgeschlagenen Problemen: Die Ziele haben Ordinal- Beziehungen zueinander. Es gibt einen größeren Unterschied zwischen Bronze und Gold als zwischen Silber und Gold. Ebenso sollten unsere falschen Vorhersagen aus Sicht des Modells, das wir erstellen möchten, ordinale Beziehungen haben. Wenn wir vorhersagen, dass ein Kleidungsstück einem Kunden zu groß sein wird, und wir mit unserer Vorhersage falsch liegen, dann ist es wahrscheinlicher, dass das Kleidungsstück dem Kunden passt, als dass wir uns völlig geirrt haben, sodass das Kleidungsstück zu klein warfare.
Diese Klasse von Problemen nennt man ordinale Regression. Obwohl sie in der Industrie weit verbreitet sind, mangelt es an Werkzeugen und Schulungen zur Verwendung dieser Modelle. Außerdem sind die vorhandenen Werkzeuge ziemlich unflexibel, da man in den Arten von Modellen und Techniken, die verwendet werden können, eingeschränkt ist. Ich habe ein etwas idealistisches Ziel, alle maßgeschneiderten Methoden des maschinellen Lernens, für die die Leute früher lineare Modelle und manuell berechnete Gradienten verwendet haben, zu übernehmen und diese Modelle stattdessen mithilfe eines Deep-Studying-Frameworks mit benutzerdefinierten Verlustfunktionen neu zu schreiben, die durch stochastischen Gradientenabstieg (SGD) optimiert werden können. Dies würde es den Leuten ermöglichen, über lineare Modelle hinauszugehen (z. B. zu tiefen neuronalen Netzwerken) und alle Vorteile von SGD (ADAM, Batch-Norm, Skalierung usw.) zu nutzen. Außerdem möchte ich dies alles in einem scikit-lernen-kompatible Weise, weil ich ihre API einfach liebe.
Um meinen Standpunkt zu verdeutlichen, schauen wir uns die einzige scikit-learn-kompatible Bibliothek an, die ich finden konnte und die für ordinale Regressionsmodelle geeignet ist. Mord. Verstehen Sie mich nicht falsch, diese Bibliothek ist großartig und schnell und wurde von einem überprüfbarer Experte in ordinalen Regressionsmodellen. Alle verfügbaren Modelle sind jedoch lineare Modelle mit L2-Regularisierung. Was ist, wenn ich ein Deep-Studying-Modell dort einfügen möchte? Was ist, wenn ich mit LASSO Sparsity induzieren möchte? Ich müsste die Zielfunktionen und zugehörigen Gradienten manuell berechnen und eine brandneue Klasse in der Bibliothek erstellen. Wenn ich stattdessen eine mit ordinaler Regression kompatible Verlustfunktion angemessen definieren kann, kann ich jedes der Deep-Studying-Frameworks verwenden, die Autodifferenzierung verwenden, um jedes gewünschte Modell zu optimieren. Und ich möchte dies auf große Datenmengen skalieren können, was die Stan Und pymc3 Implementierungen.
Das habe ich additionally getan und eine kleine Bibliothek erstellt Raumschneider um ordinale Regressionsmodelle in PyTorch zu implementieren. In diesem Beitrag werde ich erklären, wie ordinale Regression funktioniert, zeigen, wie ich das Modell in PyTorch implementiert habe, das Modell mit verbrennen um es in einen Scikit-Be taught-Schätzer umzuwandeln und dann einige Ergebnisse anhand eines vorgefertigten Datensatzes zu teilen.
Von der binären zur ordinalen Regression
Es gibt eine Reihe von Möglichkeiten, ordinale Regressionsprobleme zu lösen, und ich werde in diesem Beitrag nur eine Methode durchgehen. Ich fand dies Papier das wurde erwähnt in mord um eine gute Einführung in die Lösung dieser Probleme zu geben. Für die in diesem Abschnitt verwendete Technik habe ich auf Folgendes verwiesen Papier vom Autor von mord, Fabian Pedregosa. Obwohl er diese Technik nicht erfunden hat, waren die zitierten Artikel kostenpflichtig, sodass ich nicht für sie bürgen kann.
Die Hauptidee hinter der ordinalen Regression besteht darin, dass wir lernen, unseren Vorhersageraum aufzuteilen, indem wir cutpoints. Aber bevor wir darauf eingehen, schauen wir uns kurz die binäre logistische Regression an, bei der wir zwei Zielklassen haben, 0 Und 1. Erinnern Sie sich, dass wir bei der logistischen Regression ein lineares Modell $f(mathbf{X}) = mathbf{X} cdot boldsymbol{beta} $ haben, das eine Designmatrix $mathbf{X}$ und einen Vektor von Koeffizienten $boldsymbol{beta}$ in eine einzelne Zahl umwandelt, die irgendwo zwischen negativer und positiver Unendlichkeit liegt ($mathbb{R}$). Die Ausgabe dieses linearen Modells wird dann durch eine logistische Funktion $sigma$ geleitet, die den Wertebereich zwischen 0 und 1 abbildet:
$$ sigma(f(mathbf{X})) = frac{1}{1 + e^{-mathbf{X} cdot boldsymbol{beta} }} $$
Diese Funktion sieht wie folgt aus:
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import numpy as np
plt.ion()
plt.rcParams('determine.figsize') = (8, 5)
plt.rcParams('axes.titlesize') = 20
plt.rcParams('axes.labelsize') = 18
plt.rcParams('legend.fontsize') = 16
plt.rcParams('xtick.labelsize') = 14
plt.rcParams('ytick.labelsize') = 14
num_points = 101
f = np.linspace(-12, 12, num_points)
sigma = lambda f: 1 / (1 + np.exp(-f))
plt.plot(f, sigma(f));
plt.ylabel('$sigma(f)$');
plt.xlabel('$f$');
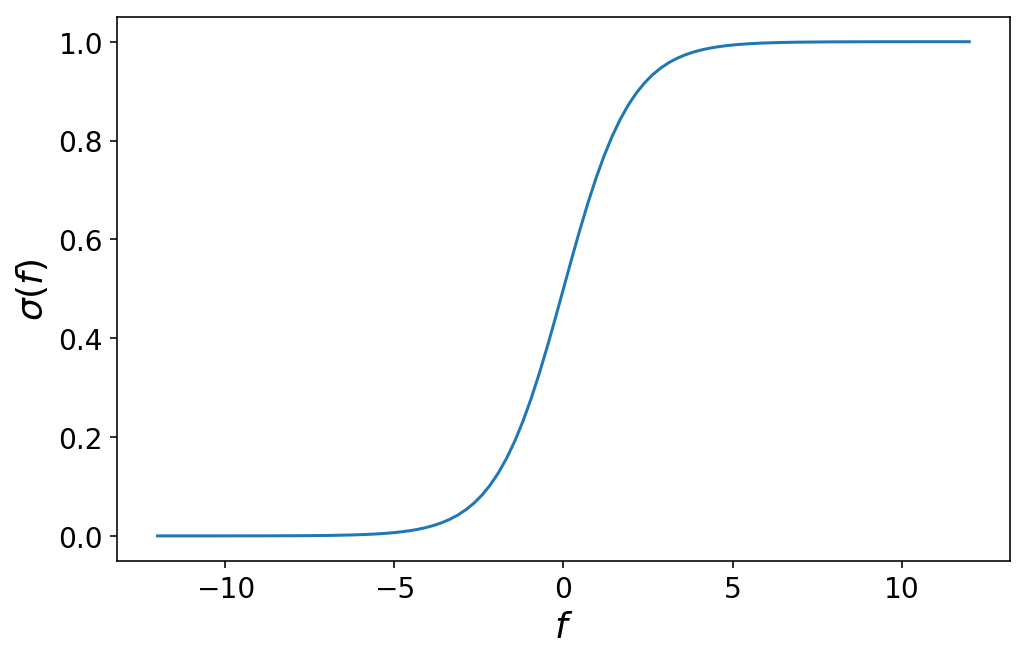
Durch etwas Mathematik kann man sich davon überzeugen, dass die Wahl eines bestimmten Wertes von f entspricht der Wahrscheinlichkeit dass die Beobachtung, die produziert f gehört zur Klasse 1Wir schreiben das als
$$P(y = 1) = sigma(f)$$
Die Wahrscheinlichkeit, dass die Beobachtung zur Klasse gehört 0 Ist
$$ start{aligned} P(y = 0) & = 1 – P(y = 1) cr & = 1 – sigma(f) finish{aligned} $$
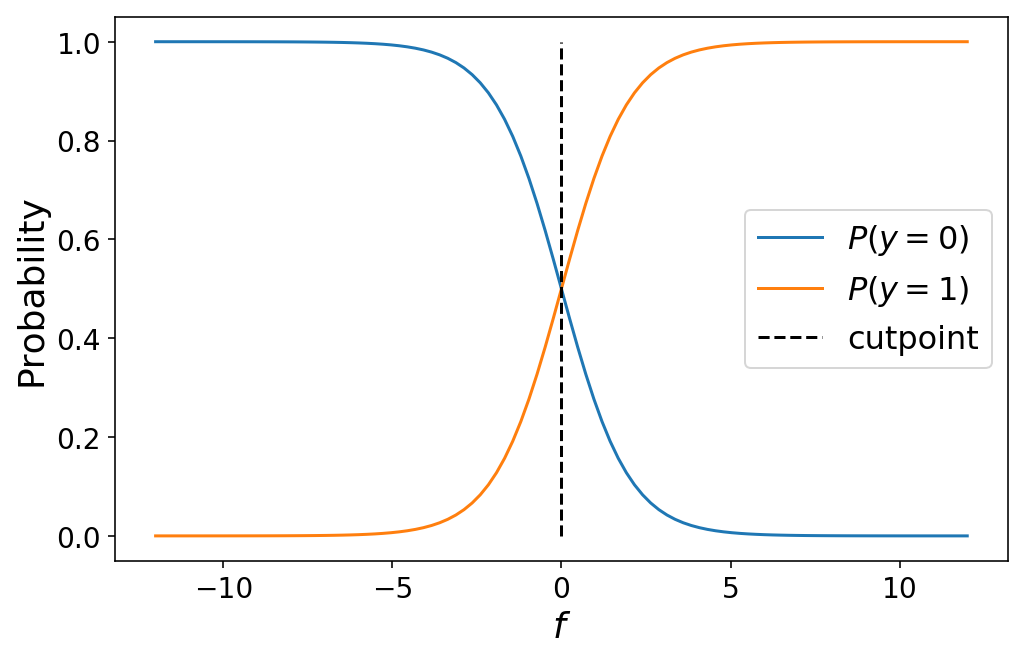
Der Wert von $f = 0$ ist insofern besonders, als er den genauen Kreuzungspunkt markiert, an dem die Beobachtung mit einer Wahrscheinlichkeit von 50 % zu einer der beiden Klassen gehört. 0 oder Klasse 1. In der Sprache der ordinalen Regression können wir $f = 0$ als Schnittpunkt die unseren Vorhersageraum zwischen Klasse 0 Und 1:
plt.plot(f, 1 - sigma(f));
plt.plot(f, sigma(f));
plt.plot((0, 0), (0, 1), 'k--');
plt.legend(('$P(y = 0)$', '$P(y = 1)$', 'cutpoint'))
plt.ylabel('Likelihood');
plt.xlabel('$f$');
Der Übergang von der binären Klassifizierung zur ordinalen Regression mit 3+ Klassen erfordert lediglich die Definition weiterer Trennpunkte, um unseren Vorhersageraum in den Raum der „Klassenwahrscheinlichkeit“ aufzuteilen. Für $Okay$ Klassen haben wir $Okay – 1$ Trennpunkte. Die Wahrscheinlichkeit, dass eine Beobachtung zur Klasse $okay$ gehört, ist gegeben durch Kumulative Logistikverbindungsfunktion:
$$ P(y = okay) = start{instances} sigma(c_{okay} – f(mathbf{X})),, textual content{wenn } okay = 0 cr sigma(c_{okay} – f(mathbf{X})) – sigma(c_{okay – 1} – f(mathbf{X})) ,, textual content{wenn } 0 < okay < Okay cr 1 - sigma(c_{Okay - 1} - f(mathbf{X})) ,, textual content{wenn } okay = Okay cr finish{instances} $$
Zu beachten ist, dass dies perfekt auf eine binäre Klassifizierung zusammenfällt, falls wir nur zwei Klassen haben (probieren Sie es selbst aus!). Das folgende Diagramm zeigt die Klassenwahrscheinlichkeiten für ein ordinales Regressionsmodell mit drei Klassen:
def plot_ordinal_classes(f, cutpoints):
num_classes = len(cutpoints) + 1
labels = ()
for idx in vary(num_classes):
if idx == 0:
plt.plot(f, sigma(cutpoints(0) - f));
elif idx == num_classes - 1:
plt.plot(f, 1 - sigma(cutpoints(-1) - f));
else:
plt.plot(f, sigma(cutpoints(idx) - f) - sigma(cutpoints(idx - 1) - f));
labels.append(f'$P(y = {idx})$')
for c in cutpoints:
plt.plot((c, c), (0, 1), 'k--')
labels.append('cutpoints')
plt.legend(labels);
plt.ylabel('Likelihood');
plt.xlabel('$f$');
cutpoints = (-2, 2)
plot_ordinal_classes(f, cutpoints)
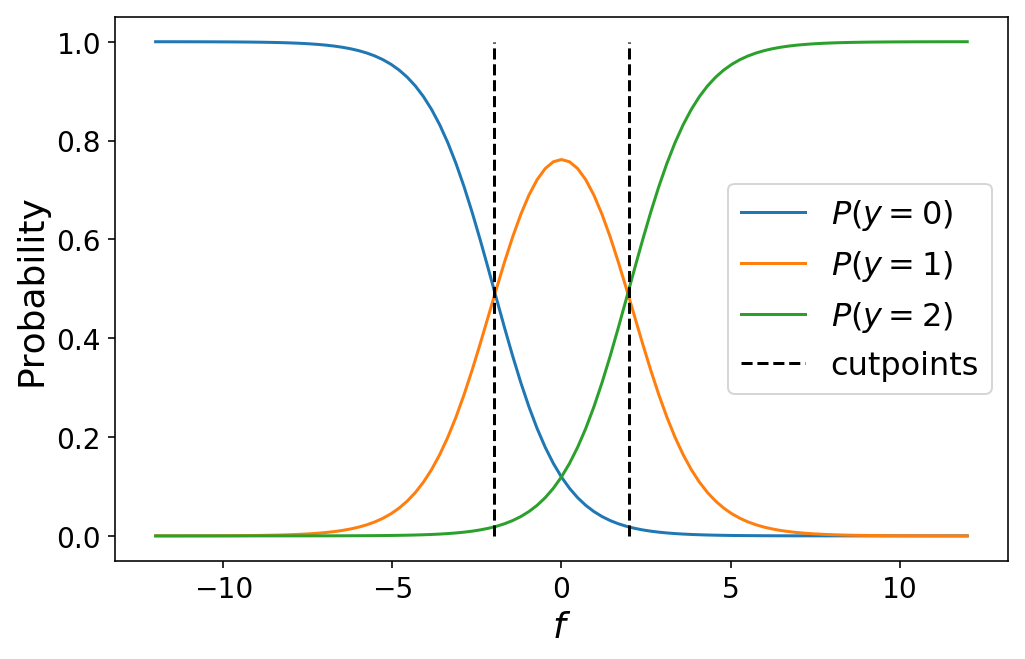
Während ich die Trennpunkte oben manuell definiert habe, würden wir in der Praxis lernen die optimalen Werte für die Schnittpunkte als Teil unseres maschinellen Lernproblems (darüber werden wir im nächsten Abschnitt sprechen). Durch Variieren der Schnittpunkte variieren die Klassenwahrscheinlichkeiten. Dies kann manchmal zu nicht intuitiven Ergebnissen führen, wenn die Schnittpunkte nahe beieinander liegen, z. B. wenn eine bestimmte Klasse nie die wahrscheinlichste Klasse für einen beliebigen Wert von $f$ ist.
plot_ordinal_classes(np.linspace(-5, 5, 101), (-0.5, 0.5))
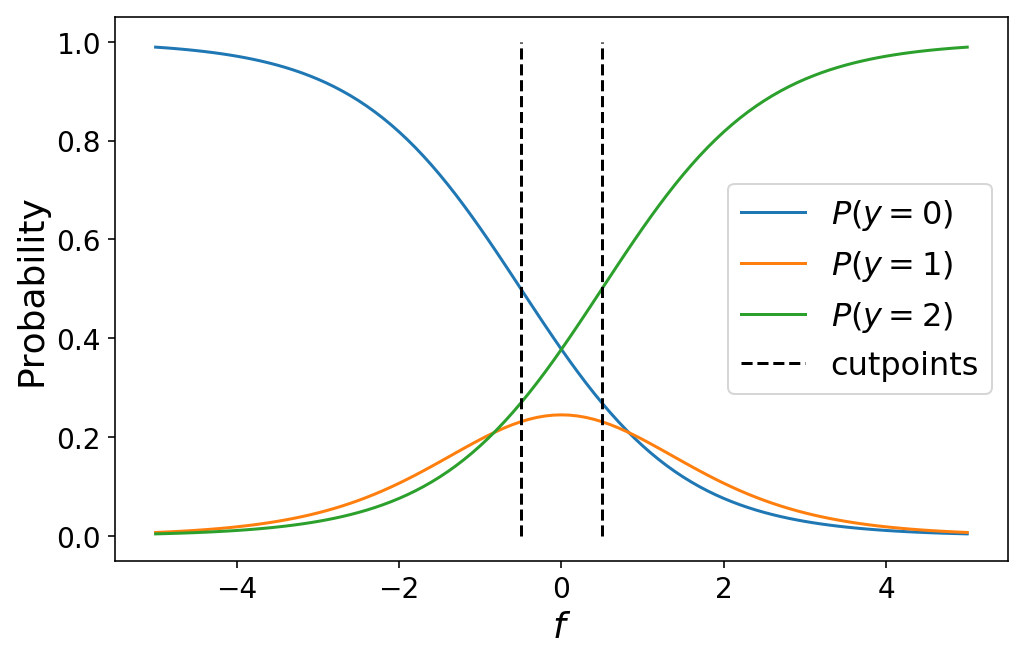
Die folgende Animation zeigt die Klassenwahrscheinlichkeiten für ein 5-Klassen-Modell, während wir die Schnittpunkte variieren.
Ordinalregression lernen
Jetzt, da wir unser Modell haben, das ordinale Klassenwahrscheinlichkeiten vorhersagt, ist es nur noch ein kleiner Schritt zu Lernen ein Modell. Wir müssen einfach eine Verlustfunktion definieren und minimieren. Unsere Verlustfunktion ist die unfavorable Log-Chance, die dem negativen Log der Klassenwahrscheinlichkeit entspricht, die wir für die Klasse vorhersagen, die die „wahre“ Klasse für eine bestimmte Beobachtung ist. Stellen Sie sich in Pseudocode vor, wir hätten drei Klassen und eine Vorhersage y_pred = (0.25, 0.5, 0.25) entsprechend der vorhergesagten Klassenwahrscheinlichkeit für jede der drei Klassen. Wenn y_true = 1dann ist unser Verlust -log(y_pred(1)). Dies lässt sich in PyTorch ganz einfach definieren. Anschließend müssen wir nur noch unser Modell optimieren. Und unsere Schnittpunkte über den stochastischen Gradientenabstieg (SGD).
Eine Schwierigkeit besteht darin, dass unsere Schnittpunkte in aufsteigend Ordnung. Das heißt, cutpoint(0) < cutpoint(1) < ... cutpoint(Okay-1). Das ist ein Zwang auf unser Optimierungsproblem, das von SGD nicht einfach zu handhaben ist. Mein schmutziger Hack besteht darin, die Cutpoint-Werte nach jedem Gradienten-Replace abzuschneiden, um sicherzustellen, dass sie immer in aufsteigender Reihenfolge sind. Mit mehr Zeit würde ich gerne eine mehr implementieren richtig Lösung.
Raumschneider
Lassen Sie uns noch einmal zusammenfassen, wie wir ordinale Regressionsmodelle trainieren:
- Wir erstellen ein Modell, das eine einzelne skalare Vorhersage generiert.
- Verwenden Sie die kumulative logistische Verknüpfungsfunktion, um diese skalaren Wahrscheinlichkeiten auf ordinale Klassen zuzuordnen.
- Definieren und minimieren Sie den negativen Log-Chance-Verlust, der den Vorhersagen entspricht.
- Stellen Sie sicher, dass die
cutpointsbleiben in aufsteigender Reihenfolge.
Lassen Sie uns nun durchgehen, wie das geht in Raumschneider. Wir verwenden einen Weinqualitätsdatensatz aus dem UCI-Repository, in dem jede Beobachtung ein Wein ist, der auf einer Skala von 1 bis 10 bewertet wird. Wir beginnen mit dem Herunterladen des Datensatzes, überprüfen einige der Merkmale und führen eine grundlegende Vorverarbeitung der Merkmale mithilfe des neuen Spaltentransformator In scikit-learn.
import warnings
import pandas as pd
from sklearn.compose import ColumnTransformer
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import mean_absolute_error, accuracy_score, make_scorer
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, PowerTransformer, FunctionTransformer
from skorch.callbacks import Callback, ProgressBar
from skorch.internet import NeuralNet
import torch
from torch import nn
warnings.simplefilter('ignore')
# Obtain the dataset
# !wget "https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv"
wine = pd.read_csv('winequality-red.csv', sep=';')
wine.head()
| feste Säure | flüchtige Säure | Zitronensäure | Restzucker | Chloride | freies Schwefeldioxid | Gesamtschwefeldioxid | Dichte | pH | Sulfate | Alkohol | Qualität | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 7.4 | 0,70 | 0,00 | 1.9 | 0,076 | 11.0 | 34,0 | 0,9978 | 3.51 | 0,56 | 9.4 | 5 |
| 1 | 7.8 | 0,88 | 0,00 | 2.6 | 0,098 | 25,0 | 67,0 | 0,9968 | 3.20 | 0,68 | 9,8 | 5 |
| 2 | 7.8 | 0,76 | 0,04 | 2.3 | 0,092 | 15,0 | 54,0 | 0,9970 | 3.26 | 0,65 | 9,8 | 5 |
| 3 | 11.2 | 0,28 | 0,56 | 1.9 | 0,075 | 17,0 | 60,0 | 0,9980 | 3.16 | 0,58 | 9,8 | 6 |
| 4 | 7.4 | 0,70 | 0,00 | 1.9 | 0,076 | 11.0 | 34,0 | 0,9978 | 3.51 | 0,56 | 9.4 | 5 |
Es scheint, dass jeder die Weinqualität mit einer Be aware zwischen 3 und 8 bewertet. Wir werden diese den Klassen 0 bis 5 zuordnen.
y = wine.pop('high quality')
(y.value_counts()
.sort_index()
.plot(variety='bar'));
plt.ylabel('Counts');
plt.xlabel('High quality');
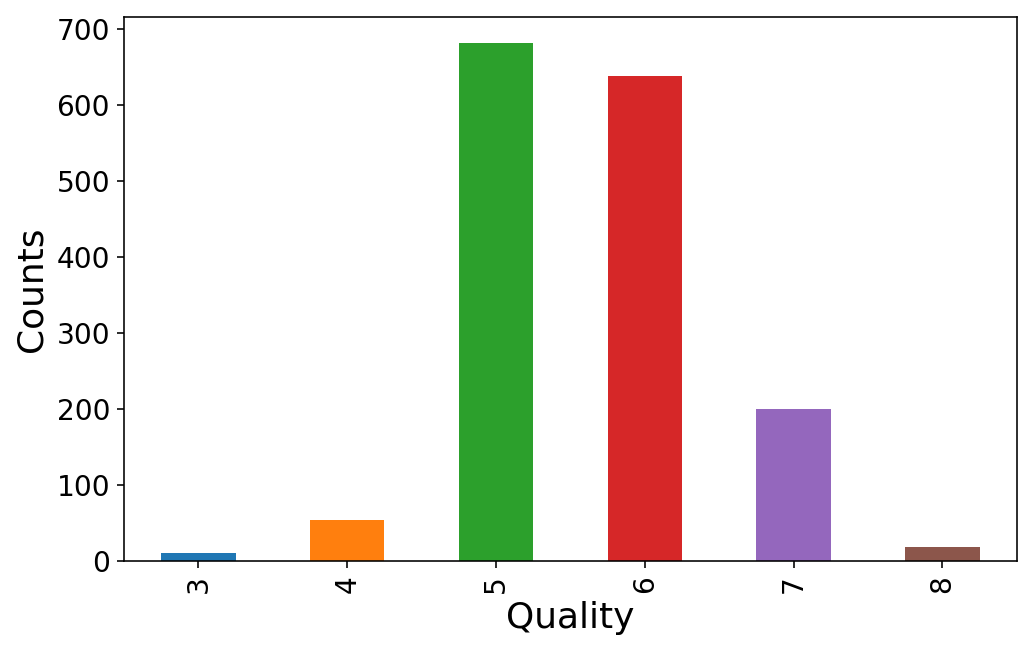
Wir werden uns die Verteilungen der 11 verschiedenen Funktionen ansehen.
wine.hist(figsize=(10, 10));
plt.tight_layout();
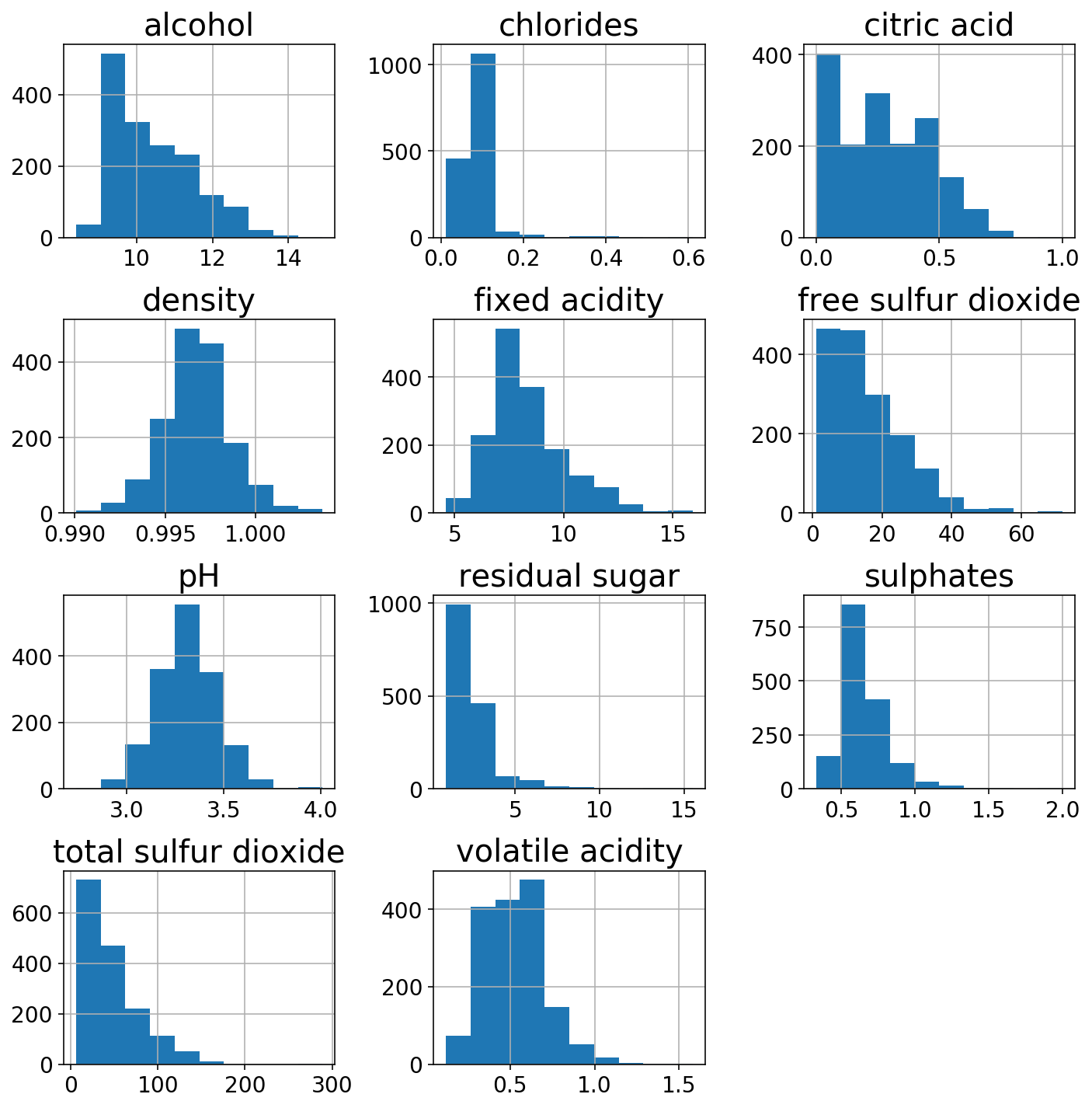
Nur um die Macht der ColumnTransformerich benutze ein StandardScaler auf den eher gaußförmigen Säulen und einem PowerTransformer auf den anderen. Die transformierten Gesichtszüge sehen etwas normaler aus.
gaussian_columns = ('alcohol', 'chlorides', 'fastened acidity',
'density',
'pH', 'sulphates', 'risky acidity')
power_columns = ('citric acid', 'free sulfur dioxide', 'residual sugar',
'whole sulfur dioxide')
column_transformer = ColumnTransformer((
('gaussian', StandardScaler(), gaussian_columns),
('energy', PowerTransformer(), power_columns)
))
X_trans = column_transformer.fit_transform(wine)
(pd.DataFrame(X_trans,
columns=gaussian_columns + power_columns)
.hist(figsize=(10, 10)));
plt.tight_layout();
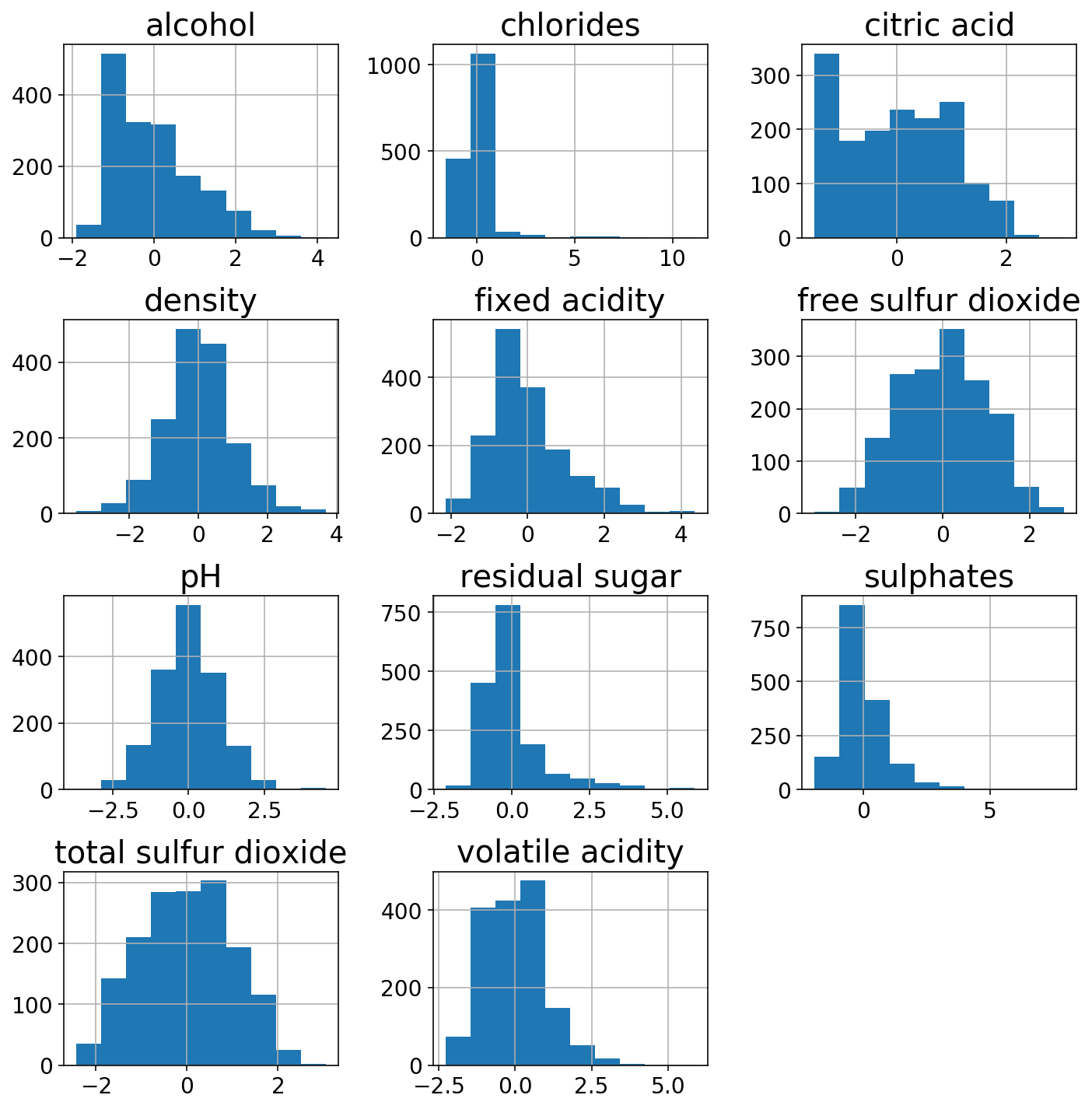
y = y.values.astype(np.lengthy).reshape(-1, 1)
# Map y from (3-8) to (0-5)
y -= y.min()
X = wine
(X_train, X_test,
y_train, y_test) = train_test_split(X, y, test_size=0.33,
stratify=y, random_state=666)
Cool, jetzt, da wir ein X Und y und einem Vorverarbeitungstransformator können wir mit dem Trainieren des Modells beginnen. Denken Sie daran, dass der erste Schritt zur ordinalen Regression ein Modell ist, das einen einzelnen Skalarwert vorhersagt. Ich werde zu diesem Zweck ein einfaches zweischichtiges neuronales Netzwerk in PyTorch erstellen.
num_features = len(gaussian_columns + power_columns)
predictor = nn.Sequential(
nn.Linear(num_features, num_features),
nn.ReLU(inplace=True),
nn.Linear(num_features, num_features),
nn.ReLU(inplace=True),
nn.Linear(num_features, 1, bias=False)
)
Mit spacecutterwir können das einpacken predictor mit dem OrdinalLogisticModel Dadurch werden Schnittpunkte erstellt und die Prädiktorausgabe durch die kumulative logistische Linkfunktion geleitet
from spacecutter.fashions import OrdinalLogisticModel
num_classes = len(np.distinctive(y))
mannequin = OrdinalLogisticModel(predictor, num_classes)
X_tensor = torch.as_tensor(X_train.values.astype(np.float32))
predictor_output = predictor(X_tensor).detach()
model_output = mannequin(X_tensor).detach()
print(predictor_output)
print(model_output)
tensor(((-4.9971),
(-1.3892),
(-1.9079),
...,
(-3.1603),
(-5.7689),
(-5.1477)))
tensor(((0.9239, 0.0467, 0.0184, 0.0069, 0.0026, 0.0015),
(0.2477, 0.2246, 0.2364, 0.1599, 0.0786, 0.0527),
(0.3562, 0.2444, 0.2029, 0.1140, 0.0505, 0.0320),
...,
(0.6593, 0.1809, 0.0944, 0.0403, 0.0157, 0.0094),
(0.9633, 0.0228, 0.0087, 0.0032, 0.0012, 0.0007),
(0.9339, 0.0407, 0.0159, 0.0060, 0.0022, 0.0013)))
Um dieses Modell zu trainieren, verwenden wir skorch das unser Modell umschließt und es als Scikit-Be taught-Schätzer kompatibel macht. Entscheidend ist, dass wir den CumulativeLinkLoss Verlustmodul von spacecutter. Zusätzlich verwenden wir eine benutzerdefinierte spacecutter Ruf zurück AscensionCallback Dadurch wird die aufsteigende Reihenfolge der Schnittpunkte beibehalten.
from spacecutter.losses import CumulativeLinkLoss
from spacecutter.callbacks import AscensionCallback
skorch_model = NeuralNet(
module=OrdinalLogisticModel,
module__predictor=predictor,
module__num_classes=num_classes,
criterion=CumulativeLinkLoss,
max_epochs=100,
optimizer_type=torch.optim.Adam,
optimizer__weight_decay=0.0,
lr=0.1,
system='cpu',
callbacks=(
('ascension', AscensionCallback()),
),
train_split=None,
verbose=0,
)
Der letzte Schritt besteht darin, alles in eine Scikit-Be taught-Pipeline zu packen. Hinweis: Ich muss einen kleinen Transformator hinzufügen, um sicherzustellen, dass die Matrizen Floats (und keine Doubles) sind, bevor sie an das Skorch-Modell übergeben werden.
def to_float(x):
return x.astype(np.float32)
pipeline = Pipeline((
('column', column_transformer),
('caster', FunctionTransformer(to_float)),
('internet', skorch_model)
))
Verwenden wir den mittleren absoluten Fehler als Bewertungskriterium und führen wir eine Rastersuche über die Anzahl der Epochen, die Lernrate und den Gewichtsabfall (auch bekannt als ~L2-Regularisierung) durch.
def mae_scorer(y_true, y_pred):
return mean_absolute_error(y_true, y_pred.argmax(axis=1))
scoring = make_scorer(mae_scorer,
greater_is_better=False,
needs_proba=True)
param_grid = {
'net__max_epochs': np.logspace(1, 3, 5).astype(int),
'net__lr': np.logspace(-4, -1, 5),
'net__optimizer__weight_decay': np.logspace(-6, -2, 4)
}
sc_grid_search = GridSearchCV(
pipeline, param_grid, scoring=scoring,
n_jobs=None, cv=5, verbose=1
)
sc_grid_search.match(X_train, y_train)
Becoming 5 folds for every of 100 candidates, totalling 500 suits
(Parallel(n_jobs=1)): Utilizing backend SequentialBackend with 1 concurrent staff.
(Parallel(n_jobs=1)): Completed 500 out of 500 | elapsed: 92.0min completed
GridSearchCV(cv=5, error_score="raise-deprecating",
estimator=Pipeline(reminiscence=None,
steps=(('column', ColumnTransformer(n_jobs=None, the rest="drop", sparse_threshold=0.3,
transformer_weights=None,
transformers=(('gaussian', StandardScaler(copy=True, with_mean=True, with_std=True), ('alcohol', 'chlorides', 'fastened acidity', 'density', 'pH', 'sulphates', 'risky ...as=True)
(3): ReLU(inplace)
(4): Linear(in_features=11, out_features=1, bias=False)
),
)))),
fit_params=None, iid='warn', n_jobs=None,
param_grid={'net__max_epochs': array(( 10, 31, 100, 316, 1000)), 'net__lr': array((0.0001 , 0.00056, 0.00316, 0.01778, 0.1 )), 'net__optimizer__weight_decay': array((1.00000e-06, 2.15443e-05, 4.64159e-04, 1.00000e-02))},
pre_dispatch="2*n_jobs", refit=True, return_train_score="warn",
scoring=make_scorer(mae_scorer, greater_is_better=False, needs_proba=True),
verbose=1)
Nachdem wir unsere Suche nun abgeschlossen haben (86 Minuten später …), untersuchen wir die Ergebnisse.
Wir können sehen, dass die Schnittpunkte angemessen voneinander getrennt und in aufsteigender Reihenfolge sind.
cutpoints = (sc_grid_search
.best_estimator_
.named_steps('internet')
.module_
.hyperlink
.cutpoints
.detach())
print(f"Cutpoints: {cutpoints}")
Cutpoints: tensor((-3.3575, -2.6696, -0.1757, 1.9482, 3.6145))
Die Genauigkeit ist für ein Multiklassenmodell in Ordnung und wir können sehen, dass wir bei unserer Bewertungsvorhersage im Durchschnitt um weniger als 0,5 daneben liegen.
y_pred = sc_grid_search.predict_proba(X_test).argmax(axis=1)
print(f'Accuracy = {accuracy_score(y_test.squeeze(), y_pred):1.4f}')
print(f'MAE = {mean_absolute_error(y_test.squeeze(), y_pred):1.4f}')
Accuracy = 0.6250
MAE = 0.3958
bins = np.arange(6)
plt.hist(y_test, bins=bins, alpha=0.5);
plt.hist(y_pred, bins=bins, alpha=0.5);
plt.legend(('y_true', 'y_pred'));
plt.ylabel('Counts');
plt.xlabel('Ordinal Class');
plt.title('spacecutter Class Distributions');
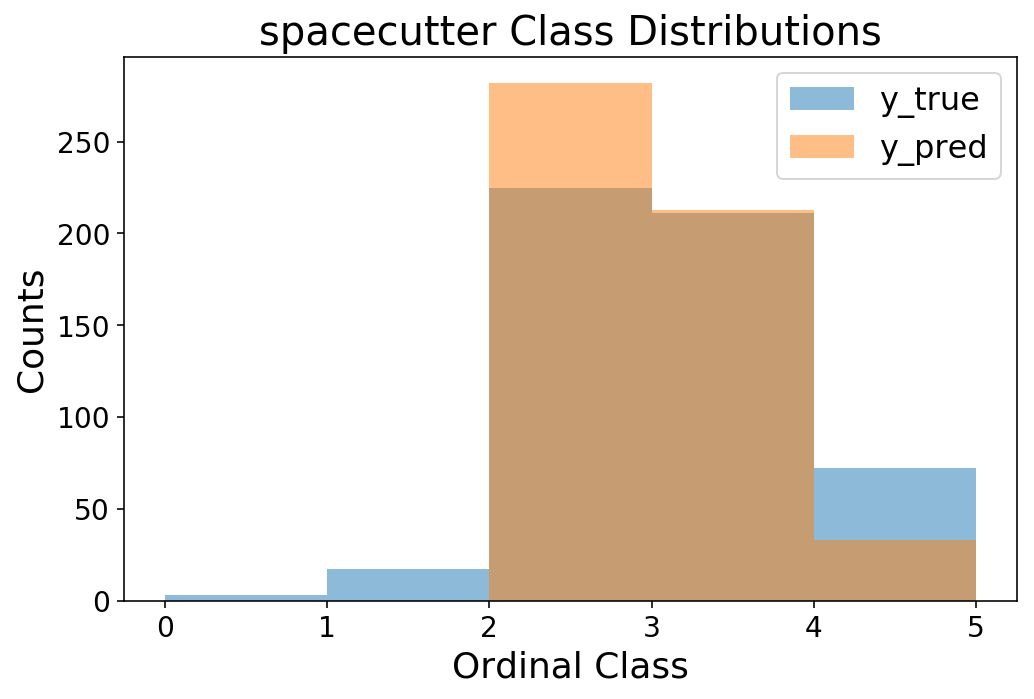
Zum Schluss noch ein kurzer Vergleich mit mord.
from mord.threshold_based import LogisticAT
pipeline = Pipeline((
('column', column_transformer),
('caster', FunctionTransformer(to_float)),
('mannequin', LogisticAT())
))
param_grid = {
'model__max_iter': np.logspace(3, 5, 5).astype(int),
'model__alpha': np.logspace(0, 4, 5)
}
mord_grid_search = GridSearchCV(
pipeline, param_grid, scoring=scoring,
n_jobs=None, cv=5, verbose=1
)
mord_grid_search.match(X_train, y_train)
Becoming 5 folds for every of 25 candidates, totalling 125 suits
(Parallel(n_jobs=1)): Utilizing backend SequentialBackend with 1 concurrent staff.
(Parallel(n_jobs=1)): Completed 125 out of 125 | elapsed: 13.2s completed
GridSearchCV(cv=5, error_score="raise-deprecating",
estimator=Pipeline(reminiscence=None,
steps=(('column', ColumnTransformer(n_jobs=None, the rest="drop", sparse_threshold=0.3,
transformer_weights=None,
transformers=(('gaussian', StandardScaler(copy=True, with_mean=True, with_std=True), ('alcohol', 'chlorides', 'fastened acidity', 'density', 'pH', 'sulphates', 'risky ...'deprecated',
validate=None)), ('mannequin', LogisticAT(alpha=1.0, max_iter=1000, verbose=0)))),
fit_params=None, iid='warn', n_jobs=None,
param_grid={'model__max_iter': array(( 1000, 3162, 10000, 31622, 100000)), 'model__alpha': array((1.e+00, 1.e+01, 1.e+02, 1.e+03, 1.e+04))},
pre_dispatch="2*n_jobs", refit=True, return_train_score="warn",
scoring=make_scorer(mae_scorer, greater_is_better=False, needs_proba=True),
verbose=1)
cutpoints = (mord_grid_search
.best_estimator_
.named_steps('mannequin')
.theta_)
print(f"Cutpoints: {cutpoints}")
Cutpoints: (-5.80087138 -3.88733054 -0.238343 2.47900366 5.45252331)
y_pred = mord_grid_search.predict(X_test)
print(f'accuracy = {accuracy_score(y_test.squeeze(), y_pred):1.3f}')
print(f'MSE = {mean_absolute_error(y_test.squeeze(), y_pred):1.3f}')
accuracy = 0.612
MSE = 0.415
bins = np.arange(6)
plt.hist(y_test, bins=bins, alpha=0.5);
plt.hist(y_pred, bins=bins, alpha=0.5);
plt.legend(('y_true', 'y_pred'));
plt.ylabel('Counts');
plt.xlabel('Ordinal Class');
plt.title('mord Class Distributions');
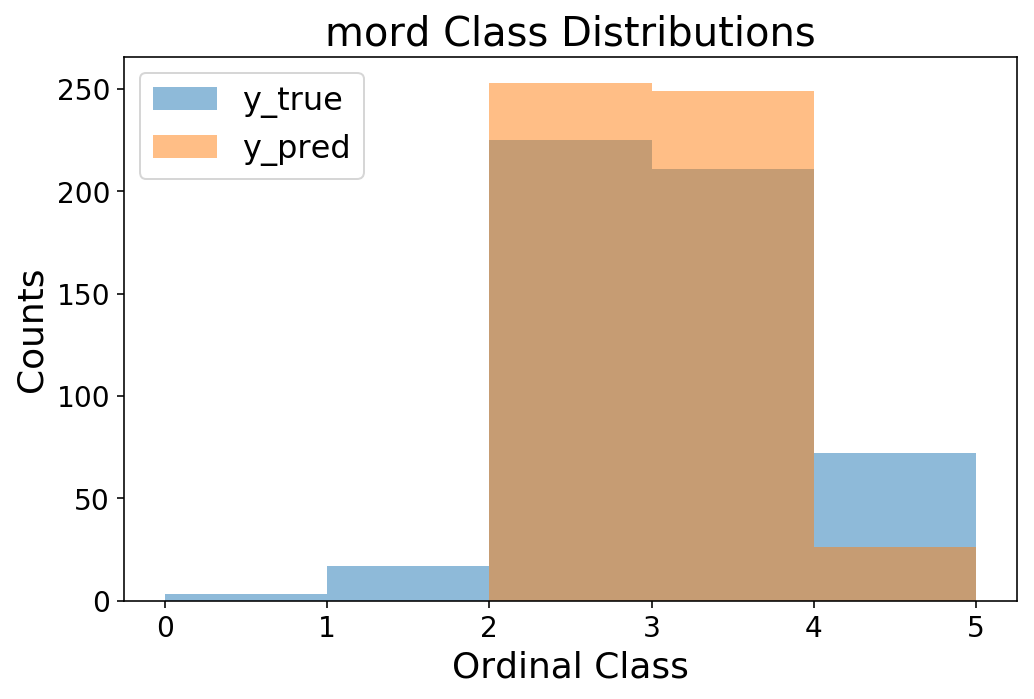
Es stellt sich heraus, dass die Ergebnisse durchaus vergleichbar sind mit spacecutter! Das ist vielleicht überraschend, aber wir haben es mit kleinen Datenmengen und wenigen Merkmalen zu tun, daher würde ich nicht erwarten, dass ein neuronales Netz besonders nützlich ist. Aber es ist eine gute Plausibilitätsprüfung, die wir durchführen, ebenso wie ein herkömmliches lineares Modell. Jetzt liegt es an Ihnen, Raumschneider Probieren Sie es aus und versuchen Sie, es auf Millionen von Beobachtungen zu skalieren 🙂
