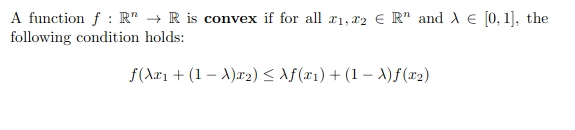Im Bereich des maschinellen Lernens besteht das Hauptziel darin, das am meisten geeignete Modell zu finden, das über eine bestimmte Aufgabe oder eine Reihe von Aufgaben trainiert wurde. Dazu muss man die Verlust-/Kostenfunktion optimieren, und dies hilft bei der Minimierung der Fehler. Man muss die Natur konkaver und konvexer Funktionen kennen, da sie diejenigen sind, die die Probleme effektiv optimieren. Diese konvexen und konkaven Funktionen bilden die Grundlage vieler Algorithmen für maschinelles Lernen und beeinflussen die Minimierung des Verlusts für die Trainingsstabilität. In diesem Artikel erfahren Sie, was konkave und konvexe Funktionen sind, welche Unterschiede sie auf die Optimierungsstrategien im maschinellen Lernen beeinflussen.
Was ist eine konvexe Funktion?
In mathematischer Begriffen ist eine realbewertete Funktion konvex, wenn das Liniensegment zwischen zwei Punkten auf dem Graphen der Funktion über den beiden Punkten liegt. In einfachen Worten ist das konvexe Funktionsdiagramm wie ein „Tasse“ oder „U“ geformt.
Eine Funktion soll nur dann konvex sein, wenn der Bereich über seinem Diagramm ein konvexer Satz ist.

Diese Ungleichheit stellt sicher, dass sich Funktionen nicht nach unten biegen. Hier ist die charakteristische Kurve für eine konvexe Funktion:

Was ist eine konkave Funktion?
Jede Funktion, die keine konvexe Funktion ist, wird als konkave Funktion bezeichnet. Mathematisch krümmt sich eine konkave Funktion nach unten oder weist mehrere Peaks und Täler auf. Oder wenn wir versuchen, zwei Punkte mit einem Section zwischen 2 Punkten im Diagramm zu verbinden, liegt die Linie unter dem Diagramm selbst.
Dies bedeutet, dass in der Teilmenge, die das gesamte Section enthält, das ihnen verbindet, zwei Punkte vorhanden ist, es ist eine konvexe Funktion, sonst ist es eine konkave Funktion.

Diese Ungleichheit verstößt gegen die Konvexitätsbedingung. Hier ist die charakteristische Kurve für eine konkave Funktion:

Unterschied zwischen konvexen und konkaven Funktionen
Im Folgenden finden Sie die Unterschiede zwischen konvexen und konkaven Funktionen:
| Aspekt | Konvexe Funktionen | Konkave Funktionen |
|---|---|---|
| Minima/maxima | Single International Minimal | Kann mehrere lokale Minima und ein lokales Most haben |
| Optimierung | Einfach zu optimieren mit vielen Standardtechniken | Schwerer zu optimieren; Standardtechniken finden möglicherweise nicht das globale Minimal |
| Häufige Probleme / Oberflächen | Glatte, einfache Oberflächen (Schüsselförmig) | Komplexe Oberflächen mit Peaks und Tälern |
| Beispiele |
f (x) = x2f (x) = eXf (x) = max (0, x) |
f (x) = sin (x) über (0, 2π) |

Optimierung im maschinellen Lernen
In maschinelles LernenDie Optimierung ist der Prozess der iterativen Verbesserung der Genauigkeit von Algorithmen für maschinelles Lernen, was letztendlich den Fehlergrad verringert. Das maschinelle Lernen zielt darauf ab, die Beziehung zwischen der Eingabe und der Ausgabe im überwachten Lernen zu finden und ähnliche Punkte zusammen im unbeaufsichtigten Lernen zusammenzuschließen. Daher ein Hauptziel der Ausbildung a Algorithmus für maschinelles Lernen ist, den Fehlergrad zwischen der vorhergesagten und der wahren Ausgabe zu minimieren.
Bevor wir weiter fortfahren, müssen wir einige Dinge wissen, z.
Verlust-/Kostenfunktionen
Die Verlustfunktion ist die Differenz zwischen dem tatsächlichen Wert und dem vorhergesagten Wert des Algorithmus für maschinelles Lernen aus einem einzigen Datensatz. Während die Kostenfunktion den Unterschied für den gesamten Datensatz aggregierte.
Verlust- und Kostenfunktionen spielen eine wichtige Rolle bei der Leitung der Optimierung eines Algorithmus für maschinelles Lernen. Sie zeigen quantitativ, wie intestine das Modell abschneidet, was als Maß für Optimierungstechniken wie Gradientenabfälle dient und wie viel die Modellparameter angepasst werden müssen. Durch die Minimierung dieser Werte erhöht das Modell allmählich seine Genauigkeit, indem die Differenz zwischen vorhergesagten und tatsächlichen Werten verringert wird.

Konvexe Optimierungsvorteile
Konvexe Funktionen sind besonders vorteilhaft, da sie eine globale Minima haben. Dies bedeutet, dass, wenn wir eine konvexe Funktion optimieren, immer sicher sein wird, dass sie die beste Lösung finden, die die Kostenfunktion minimiert. Dies macht die Optimierung viel einfacher und zuverlässiger. Hier sind einige wichtige Vorteile:
- Zusicherheit, globale Minima zu finden: In konvexen Funktionen gibt es nur eine Minima, was bedeutet, dass die lokale Minima und die globale Minima gleich sind. Diese Eigenschaft erleichtert die Suche nach der optimalen Lösung, da sich keine Sorgen machen muss, in lokalen Minima zu stecken.
- Starke Dualität: Die konvexe Optimierung zeigt, dass starke Dualität die ursprüngliche Lösung eines Issues leicht mit dem relevanten ähnlichen Drawback zusammenhängen kann.
- Robustheit: Die Lösungen der konvexen Funktionen sind robuster für Änderungen im Datensatz. In der Regel führen die kleinen Änderungen in den Eingabedaten nicht zu großen Änderungen der optimalen Lösungen und verarbeitet diese Szenarien problemlos.
- Zahlenstabilität: Die Algorithmen der konvexen Funktionen sind im Vergleich zu den Optimierungen häufig numerisch stabiler, was in der Praxis zu zuverlässigeren Ergebnissen führt.
Herausforderungen mit konkave Optimierung
Das Hauptproblem, mit dem konkave Optimierung konfrontiert ist, ist das Vorhandensein mehrerer Minima- und Sattelpunkte. Diese Punkte erschweren es, die globale Minima zu finden. Hier sind einige wichtige Herausforderungen in konkaven Funktionen:
- Höhere Rechenkosten: Aufgrund der Deformität des Verlustes erfordern konkave Probleme häufig mehr Iterationen, bevor die Chancen auf die Suche nach besseren Lösungen erhöht werden. Dies erhöht auch die Zeit und den Berechnungsbedarf.
- Lokale Minima: Konkave Funktionen können mehrere lokale Minima haben. Daher können die Optimierungsalgorithmen in diesen suboptimalen Punkten leicht eingeschlossen werden.
- Sattelpunkte: Sattelpunkte sind die flachen Regionen, in denen der Gradient 0 beträgt, aber diese Punkte sind weder lokaler Minima noch Maxima. Daher können die Optimierungsalgorithmen wie Gradientenabstieg dort hängen bleiben und länger dauern, bis diese Punkte entkommen.
- Keine Zusicherung, globale Minima zu finden: Im Gegensatz zu den konvexen Funktionen garantieren konkave Funktionen nicht, um die globale/optimale Lösung zu finden. Dies erschwert die Bewertung und Überprüfung.
- Empfindlich gegenüber Initialisierung/Ausgangspunkt: Der Ausgangspunkt beeinflusst das Endergebnis der Optimierungstechniken am meisten. Daher kann eine schlechte Initialisierung zu einer Konvergenz zu einem lokalen Minima oder einem Sattelpunkt führen.
Strategien zur Optimierung konkaver Funktionen
Die Optimierung einer konkaven Funktion ist aufgrund seiner mehreren lokalen Minima, Sattelpunkte und anderer Probleme sehr schwierig. Es gibt jedoch mehrere Strategien, die die Wahrscheinlichkeit erhöhen können, optimale Lösungen zu finden. Einige von ihnen werden unten erklärt.
- Sensible Initialisierung: Durch die Auswahl von Algorithmen wie Xavier oder He -Initialisierungstechniken kann man das Drawback des Ausgangspunkts vermeiden und die Wahrscheinlichkeit verringern, an lokalen Minima- und Sattelpunkten festzuhalten.
- Verwendung von SGD und seinen Varianten: SGD (Stochastic Gradient Descent) führt zufällig, was dem Algorithmus hilft, lokale Minima zu vermeiden. Außerdem können fortschrittliche Techniken wie Adam, RMSProp und Impuls die Lernrate anpassen und bei der Stabilisierung der Konvergenz helfen.
- Lernrateplanung: Die Lernrate ist wie die Schritte, um die lokale Minima zu finden. Die iterativ ausgewählte Auswahl der optimalen Lernrate hilft bei der reibungsloseren Optimierung mit Techniken wie Stufenabfall und Cosinus -Glühen.
- Regularisierung: Techniken wie L1- und L2 -Regularisierung, Ausfall und Stapelnormalisierung verringern die Wahrscheinlichkeit einer Überanpassung. Dies verbessert die Robustheit und Verallgemeinerung des Modells.
- Gradientenausschnitt: Deep Studying steht vor einem wichtigen Drawback der explodierenden Gradienten. Das Gradientenausschnitt steuert dies, indem die Gradienten vor dem Maximalwert geschnitten/begrenzt werden und ein stabiles Coaching gewährleistet.
Abschluss
Das Verständnis des Unterschieds zwischen konvexen und konkaven Funktionen ist wirksam zur Lösung von Optimierungsproblemen im maschinellen Lernen. Konvexe Funktionen bieten einen stabilen, zuverlässigen und effizienten Weg zu den globalen Lösungen. Konkave Funktionen haben ihre Komplexität wie lokale Minima- und Sattelpunkte, die fortgeschrittenere und adaptivere Strategien erfordern. Durch die Auswahl der Sensible -Initialisierung, adaptive Optimierer und bessere Regularisierungstechniken können wir die Herausforderungen der konkaven Optimierung mildern und eine höhere Leistung erzielen.
Melden Sie sich an, um weiter zu lesen und Experten-Kuratinhalte zu genießen.