Was ist KDE -Handlung? – Analytics Vidhya

Das Verständnis der Datenverteilung ist einer der wichtigsten Aspekte bei der Durchführung von Datenanalysen. Das Visualisieren der Verteilung hilft uns, die Muster, Traits und Anomalien zu verstehen, die in Rohzahlen verborgen sein könnten. Während Histogramme häufig für diesen Zweck verwendet werden, können sie manchmal zu blockig sein, um einige subtile Particulars anzuzeigen. Die Kerneldichteschätzung (KDE) -Plots bieten eine glattere und genauere Möglichkeit, um kontinuierliche Daten zu visualisieren, indem die Funktion der Wahrscheinlichkeitsdichte geschätzt wird. Auf diese Weise können Datenwissenschaftler und Analysten wichtige Merkmale wie mehrere Peaks, Schiefe und Ausreißer klarer sehen. Das Lernen, KDE -Plots zu verwenden, ist eine wertvolle Fähigkeit, um Datenersichten besser zu verstehen. In diesem Artikel werden wir KDE -Plots und ihre Implementierungen durchgehen.

Was sind Kerneldichteschätzungen (KDE) Plots?

Die Kerneldichteschätzung (KDE) ist eine nichtparametrische Methode zur Schätzung der Wahrscheinlichkeitsdichtefunktion (PDF) einer kontinuierlichen Zufallsvariablen. KDE macht einfach eine glatte Kurve (Dichteschätzung), die sich der Datenverteilung annähert, anstatt getrennte Behälter wie in einem Histogramm zu verwenden. In Bezug auf die Konzept haben wir an jedem Datenpunkt einen „Kernel“ (eine glatte und symmetrische Funktion) und fügen sie hinzu, um eine kontinuierliche Dichte zu bilden. Mathematisch, wenn wir Datenpunkte haben X₁,…,X_NAnwesend Dann der KDE an einem Punkt X Ist:

Wo Okay ist der Kernel (hauptsächlich eine Glockenfunktion) und H ist die Bandbreite (ein Smoothness -Parameter). Da für die Verteilung keine feste Type wie „regular“ oder „exponentiell“ entnommen wird, wird KDE als nicht parametrischer Schätzer bezeichnet. KDE „glättet ein Histogramm“, indem jeder Datenpunkt in einen kleinen Hügel umwandelt. Alle diese Hügel zusammen machen die Gesamtdichte (wie aus dem folgenden Diagramm ersichtlich ist).

Verschiedene Arten von Kernelfunktionen werden gemäß dem Anwendungsfall verwendet. Zum Beispiel ist der Gaußsche (oder normale) Kernel aufgrund seiner Glätte beliebt, aber andere wie Epanechnikov (parabolisch), einheitlich, dreieckig, bigewicht oder sogar Triweight können auch verwendet werden. Standardmäßig passen viele Bibliotheken mit einem Gaußschen Kernel, was bedeutet, dass jeder Datenpunkt der Schätzung eine glockenförmige Beule verleiht. Epanechnikov -Kernel minimiert den mittleren quadratischen Fehler zwischen allen, aber dennoch wird der Gaußsche nur aus Gründen der Bequemlichkeit ausgewählt.

Dichtediagramme sind sehr hilfreich bei der Analyse von Daten, um die Type einer Verteilung anzuzeigen. Sie eignen sich intestine für große Datensätze und können Dinge (wie mehrere Peaks oder lange Schwänze) anzeigen, damit sich ein Histogramm verbergen könnte. Zum Beispiel können KDE-Diagramme bimodale oder verzerrte Formen fangen, die Ihnen über Untergruppen oder Ausreißer erzählen. Bei der Erforschung einer neuen numerischen Variablen ist das Auftreten von KDE oft eines der ersten Dinge, die Menschen tun. In einigen Bereichen (wie Signalverarbeitung oder Ökonometrie) wird KDE auch als Parzen-Rosenblatt-Fenstermethode bezeichnet.

Wichtige Konzepte

Hier sind die wichtigsten Dinge, die Sie beachten sollten, wenn Sie verstehen, wie KDE -Handlung funktioniert:

• Nichtparametrische PDF-Schätzung: KDE nimmt nicht die zugrunde liegende Verteilung an. Es erstellt eine reibungslose Schätzung direkt aus den Daten.
• Kernelfunktionen: Ein Kernel Okay (z. B. Gaußsche) ist eine symmetrische Gewichtungsfunktion. Zu den häufigen Auswahlmöglichkeiten gehören Gaußsche, Epanechnikov, Uniform usw. Die Wahl hat einen geringen Einfluss auf das Ergebnis, solange die Bandbreite angepasst ist.
• Bandbreite (Glättung): Der Parameter H (oder gleichwertig BW) skaliert den Kernel. Größer H ergibt glattere (breitere) Kurven; kleiner H ergibt engere, detailliertere Kurven. Die optimale Bandbreite skaliert oft wie n^–1/5.
• Vorbiegungsvarianz-Kompromiss: Eine wichtige Überlegung ist das Ausgleich von Particulars im Vergleich zu Glätte: zu klein H führt zu einer lauten Schätzung; Zu groß h kann wichtige Peaks oder Täler überflutet.

Verwenden von KDE -Diagrammen in Python

Sowohl Seeborn (gebaut auf Matplotlib) als auch Pandas machen es einfach, KDE -Diagramme in zu erstellen Python. Jetzt werde ich einige Verwendungsmuster, Parameter und Anpassungsspitzen zeigen.

Seeborns Kdeplot

Erstens verwenden Sie seaborn.kdeplot Funktion. Diese Funktion zeichnet univariate (oder bivariate) KDE -Kurven für einen Datensatz dar. Intern werden standardmäßig einen Gaußschen Kernel verwendet und unterstützt viele andere Optionen. Zum Beispiel die Verteilung der Verteilung der sepal_width Variable aus dem Iris -Datensatz.

Univariate KDE -Plot mit Seeborn (Beispiel für IRIS -Datensatz)

Das folgende Beispiel zeigt, wie ein KDE -Diagramm für eine einzelne kontinuierliche Variable erstellt wird.

import seaborn as sns

import matplotlib.pyplot as plt

# Load instance dataset

df = sns.load_dataset('iris')

# Plot 1D KDE

sns.kdeplot(information=df, x='sepal_width', fill=True)

plt.title("KDE of Iris Sepal Width")

plt.xlabel("Sepal Width")

plt.ylabel("Density")

plt.present()

Aus dem vorherigen Bild können wir eine glatte Dichtekurve von der sehen speal_width Werte. Auch die fill=True Argument prägt den Bereich unter der Kurve und wenn dies der Fall ist fill = FalseNur die dunkelblaue Linie wäre sichtbar gewesen.

Vergleich von KDE -Diagrammen über Kategorien hinweg

Bisher haben wir einfache univariate KDE -Handlungen gesehen. Lassen Sie uns nun eine der mächtigsten Verwendungszwecke von Seeborns sehen kdeplot Methode, die ihre Fähigkeit ist, Verteilungen über Untergruppen hinweg zu vergleichen Farbton Parameter.

Angenommen, wir möchten analysieren, wie sich die Verteilung der gesamten Restaurantrechnungen zwischen dem Mittag- und der Dinners unterscheidet. Lassen Sie uns dafür das verwenden Tipps Datensatz. Damit können wir zwei KDE -Diagramme, eine zum Mittagessen und eine zum Abendessen, auf denselben Achsen zum direkten Vergleich überlagern.

import seaborn as sns

import matplotlib.pyplot as plt

suggestions = sns.load_dataset('suggestions')

sns.kdeplot(information=suggestions, x='total_bill', hue="time", fill=True,

common_norm=False, alpha=0.5)

plt.title("KDE of Complete Invoice (Lunch vs Dinner)")

plt.present()

So können wir sehen, dass der obige Code zwei Dichtekurven überlagert. Der fill=True Farbtöne unter jeder Kurve, um den Unterschied sichtbarer zu machen, common_norm= False stellt sicher, dass die Dichte jeder Gruppe unabhängig skaliert wird und alpha=0.5 Fügt Transparenz hinzu, sodass die überlappenden Regionen leicht zu interpretieren sind.

Sie können auch mit a number of = ‚layer‘, ’stapel‘ oder ‚füllen‘ experimentieren, um zu ändern, wie mehrere Dichten gezeigt werden.

Pandas und Matplotlib

Wenn Sie mit Pandas arbeiten, können Sie auch integrierte Plotten verwenden, um KDE-Diagramme zu erhalten. Eine Pandas -Serie hat eine plot(variety=’density’) oder plot.density() Methode, die als Wrapper für die relevanten Methoden in fungiert Matplotlib.

Code:

import pandas as pd

import numpy as np

information = np.random.randn(1000) # 1000 random factors from a standard distribution

s = pd.Sequence(information)

s.plot(variety='density')

plt.title("Pandas Density Plot")

plt.xlabel("Worth")

plt.present()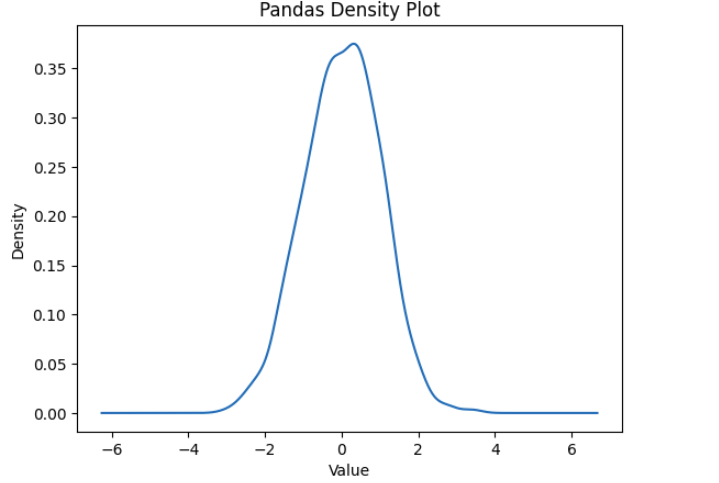

Alternativ können wir KDE manuell verwenden und verabschieden Scipy‚S gaussian_kde Verfahren.

import numpy as np

from scipy.stats import gaussian_kde

information = np.concatenate((np.random.regular(-2, 0.5, 300), np.random.regular(3,

1.0, 500)))

kde = gaussian_kde(information, bw_method=0.3) # bandwidth generally is a issue or

'silverman', 'scott'

xs = np.linspace(min(information), max(information), 200)

density = kde(xs)

plt.plot(xs, density)

plt.title("Guide KDE through scipy")

plt.xlabel("Worth"); plt.ylabel("Density")

plt.present()

Der obige Code erstellt einen bimodalen Datensatz und schätzt seine Dichte. In der Praxis verwenden Seeborn oder Pandas Die gleiche Funktionalität ist viel einfacher.

Interpretieren von KDE -Diagramm oder Kerneldichteschätzer -Diagramm

Das Lesen eines KDE -Diagramms ähnelt einem Histogramm, jedoch mit einer glatten Kurve. Die Höhe der Kurve an einem Punkt X ist proportional zur geschätzten Wahrscheinlichkeitsdichte dort. Der Bereich unter der Kurve über einen Bereich entspricht der Wahrscheinlichkeit, in diesem Bereich zu landen. Da die Kurve kontinuierlich ist, ist der genaue Wert an irgendeinem Punkt nicht so wichtig wie die Gesamtform:

• Peaks (Modi): Ein hoher Peak zeigt einen gemeinsamen Wert oder Cluster in den Daten an. Mehrere Peaks legen mehrere Modi nahe (z. B. Mischung von Subpopulationen).
• Verbreiten: Die Breite der Kurve zeigt Dispersion. Eine breitere Kurve bedeutet mehr Variabilität (größere Standardabweichung), während eine schmale, hohe Kurve bedeutet, dass die Daten eng geklustert sind.
• Schwänze: Beobachten Sie, wie schnell sich die Dichte verjüngt. Schwere Schwänze implizieren Ausreißer; kurze Schwänze implizieren begrenzte Daten.
• Vergleich von Kurven: Wenn Sie Gruppen überlagern, suchen Sie nach Verschiebungen (eine Verteilung systematisch höher oder niedriger) oder nach Unterschieden in der Type.

Anwendungsfälle und Beispiele

KDE-Diagramme haben viele nützliche Anwendungen in der täglichen Datenanalyse:

• Explorationsdatenanalyse (EDA): Wenn wir uns zum ersten Mal einen Datensatz ansehen, hilft uns KDE, zu sehen, wie die Variablen verteilt sind, unabhängig davon, ob sie regular, verzerrt oder mehr als einen Peak (multimodal) aussehen. Wie wir alle wissen, ist es wahrscheinlich die erste Aufgabe, die Verteilung Ihrer Variablen zu überprüfen, wenn Sie einen neuen Datensatz erhalten. KDE, der glatter als Histogramme ist, ist oft hilfreicher, wenn Sie versuchen, ein Gefühl für die Daten während der EDA zu bekommen.
• Vergleich von Verteilungen: KDE funktioniert intestine, wenn wir vergleichen wollen, wie sich verschiedene Gruppen verhalten. Zum Beispiel zeigt die Aufzeichnung der KDE der Testergebnisse für Jungen und Mädchen auf derselben Achse, ob es einen Unterschied in der Durchschnitts- oder Variation gibt. Seeborn macht es tremendous einfach, KDE mit verschiedenen Farben zu überlagern. KDE-Diagramme sind normalerweise weniger chaotisch als Histogramme von nebeneinander und vermitteln ein besseres Gefühl dafür, wie sich die Gruppen unterscheiden.
• Glättungshistogramme: KDE kann als eine glattere Model eines Histogramms betrachtet werden. Wenn Histogramme zu unruhig aussehen oder sich mit der Behältergröße stark ändern, gibt KDE ein stabileres und klareres Bild. Zum Beispiel könnte das obige Airbnb -Preis als Histogramm angezeigt werden, aber KDE erleichtert es viel einfacher zu interpretieren. KDE hilft bei der Erstellung einer kontinuierlicheren Schätzung der Type der Daten, die sehr praktisch ist, insbesondere wenn die Daten nicht zu groß oder zu klein sind.

Alternativen zu Kernendichteplots

Während KDE -Diagramme sehr nützlich sind, um reibungslose Schätzungen einer Verteilung zu zeigen, sind sie nicht immer das Beste. Abhängig von der Datengröße oder dem, was genau Sie versuchen, können Sie auch andere Arten von Handlungen versuchen. Hier sind ein paar gemeinsame:

Histogramme

Ehrlich gesagt, die grundlegendste Möglichkeit, sich mit Verteilungen zu befassen. Sie hacken nur die Daten in Mülleimer und zählen, wie viele Dinge in jeden Fall fallen. Einfach zu bedienen, kann aber unordentlich werden, wenn Sie zu viele Behälter oder zu wenige verwenden. Manchmal verbirgt es Muster. KDE hilft dabei, indem sie die Unebenheiten glättet.

Boxplots (auch Field-and-Whisker genannt)

Diese sind intestine, wenn Sie nur wissen möchten, wie die meisten Daten sind, erhalten Sie den Median, Quartile usw. Es ist schnell, Ausreißer zu erkennen. Aber es zeigt nicht wirklich die Type der Daten wie KDE. Immer noch nützlich, wenn Sie nicht jedes Element benötigen.

Geigediagramme

Stellen Sie sich diese wie eine ausgefallene Model von Field -Plots vor, die auch die KDE -Type zeigt. Es ist wie das Beste von beiden, Sie erhalten zusammenfassende Statistiken und ein Gefühl der Verteilung. Ich benutze diese beim Vergleich von Gruppen nebeneinander.

Teppichdiagramme

Teppichdiagramme sind einfach. Sie zeigen nur jeden Datenpunkt als kleine vertikale Linien auf der Achse. Oft, zusammen mit KDE, um zu zeigen, wo sich die tatsächlichen Datenpunkte befinden. Aber wenn Sie zu viele Daten haben, kann es irgendwie unordentlich aussehen.

Histogramm + KDE -Kombination

Einige Leute kombinieren gerne ein Histogramm mit KDE, wie ein Histogramm die Zählungen zeigt, und KDE fügt eine glatte Kurve hinzu. Auf diese Weise können sie sowohl rohe Frequenzen als auch das geglättete Muster zusammen sehen.

Ehrlich gesagt, welches Sie verwenden, hängt nur davon ab, was Sie brauchen. KDE eignet sich hervorragend für glatte Muster, aber manchmal braucht man nicht alles. Vielleicht sagt ein einfaches Field -Diagramm oder ein Histogramm genug aus, besonders wenn Sie kurz sind oder nur schnell Dinge erkunden.

Abschluss

KDE -Plots bieten eine leistungsstarke und intuitive Möglichkeit, die Verteilung kontinuierlicher Daten zu visualisieren. Im Gegensatz zu normalen Histogrammen geben sie eine glatte und kontinuierliche Kurve, indem sie die Wahrscheinlichkeitsdichtefunktion mit Hilfe von Kerneln schätzen, was subtile Muster wie Schiefe, Multimodalität oder Ausreißer leichter zu bemerken. Unabhängig davon, ob Sie explorative Datenanalysen durchführen, Verteilungen vergleichen oder Anomalien finden, sind KDE -Diagramme sehr hilfreich. Werkzeuge wie Seeborn oder Pandas Machen Sie es ganz einfach, sie zu erstellen und zu verwenden.

Hallo, ich bin Janvi, ein leidenschaftlicher Information -Science -Fanatic, der derzeit bei Analytics Vidhya arbeitet. Meine Reise in die Daten der Daten begann mit einer tiefen Neugier darüber, wie wir aus komplexen Datensätzen sinnvolle Erkenntnisse herausholen können.