Wie das rekursive Denken von TRM beweist, dass weniger mehr ist

Glaubst du, das ist klein? neuronales Netzwerk (wie TRM) bei Argumentationsaufgaben um ein Vielfaches größere Modelle übertreffen kann? Wie ist es möglich, dass Milliarden von LLM-Parametern eine so kleine Anzahl bescheidener Millionen-Parameter-Iterationen haben, die Rätsel lösen?

„Derzeit leben wir in einer skalierungsbesessenen Welt: Mehr Daten. Mehr GPUs bedeuten größere und bessere Modelle. Dieses Mantra hat bisher den Fortschritt in der KI vorangetrieben.“

Aber manchmal ist weniger wirklich mehr, und die Ting Recursive Fashions (TRMs) sind markante Beispiele für dieses Phänomen. Die Ergebnisse, wie darin bewiesen diesen Berichtsind leistungsstark: TRMs erreichen eine Genauigkeit von 87,4 % bei Sudoku-Excessive und 45 % bei ARC-AGI-1 und übertreffen gleichzeitig die Leistung größerer hierarchischer Modelle, während einige hochmoderne Modelle wie DeepSeek R1, Claude und o3-mini bei Sudoku 0 % erzielten. Und DeepSeek R1 erreichte 15,8 % auf ARC-1 und nur 1,3 % auf ARC-2, während ein TRM 7M-Modell eine Genauigkeit von 44,6 % erreicht. In diesem Weblog diskutieren wir, wie TRMs durch minimale Architektur maximale Argumentation erreichen.

Die Suche nach intelligenteren, nicht größeren Modellen

Künstliche Intelligenz ist in eine Part übergegangen, die von gigantischen Modellen dominiert wird. Die Bewegung conflict unkompliziert: Skalieren Sie einfach alles, dh Daten, Parameter, Berechnungen und Intelligenz werden entstehen.

Doch während Forscher und Praktiker beharrlich daran arbeiten, diese Grenzen zu erweitern, setzt sich eine Erkenntnis durch: Größer ist nicht immer gleich besser. Wenn es um strukturiertes Denken, Genauigkeit und schrittweise Logik geht, versagen größere Sprachmodelle oft. Die Zukunft der KI liegt möglicherweise nicht darin, wie groß wir bauen können, sondern eher darin, wie clever wir denken können. Daher stößt es auf zwei Hauptprobleme:

Das Downside bei der Skalierung großer Sprachmodelle

Große Sprachmodelle haben das Verständnis, die Zusammenfassung und die kreative Texterstellung natürlicher Sprache verändert. Sie können scheinbar Muster im Textual content erkennen und eine menschenähnliche Sprachverständlichkeit erzeugen.

Dennoch, wenn sie aufgefordert werden, sich darauf einzulassen logisches Denken Um Sudoku-Rätsel zu lösen oder Labyrinthe zu planen, lässt die Genialität dieser Modelle nach. LLMs können das nächste Wort vorhersagen, aber das bedeutet nicht, dass sie den nächsten logischen Schritt durchdenken können. Bei Rätseln wie Sudoku macht eine einzige falsch platzierte Ziffer das gesamte Raster ungültig.

Wenn Komplexität zur Barriere wird

Dieser Ineffizienz liegt die einseitige, additionally ähnliche Architektur von LLMs zugrunde; Sobald ein Token generiert wurde, ist es behoben, da keine Möglichkeit besteht, einen Fehltritt zu beheben. Ein einfacher logischer Fehler zu Beginn kann die ganze Technology verderben, genauso wie eine falsche Sudoku-Zelle das Rätsel ruiniert. Daher gewährleistet eine Vergrößerung weder Stabilität noch bessere Argumentation.

Der enorme Rechen- und Datenbedarf macht es für die meisten Forscher nahezu unmöglich, auf diese Modelle zuzugreifen. Darin liegt additionally ein Paradox, dass einige der leistungsstärksten KI-Systeme Aufsätze schreiben und Bilder malen können, aber nicht in der Lage sind, Aufgaben zu erfüllen, die selbst ein rudimentäres rekursives Modell leicht lösen kann.

Dabei geht es nicht um Daten oder Umfang; Vielmehr geht es um Ineffizienz in der Architektur und darum, dass rekursiver Intellektualismus sinnvoller sein könnte als expansiver Intellekt.

Hierarchische Argumentationsmodelle (HRM): Ein Schritt in Richtung simuliertem Denken

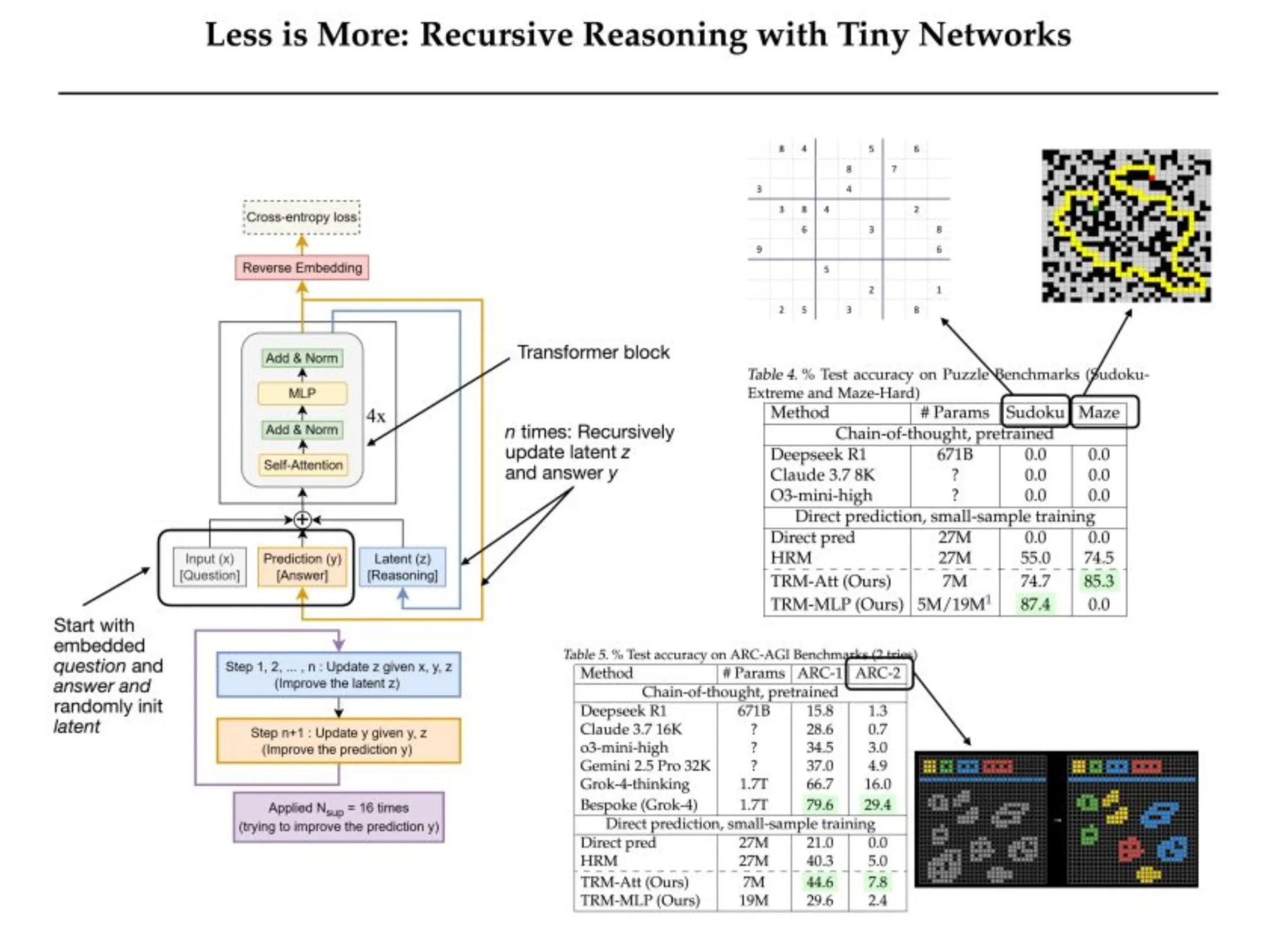
Der Hierarchisches Argumentationsmodell (HRM) ist eine aktuelle Weiterentwicklung, die gezeigt hat, wie kleine Netzwerke komplexe Probleme durch rekursive Verarbeitung lösen können. HRM verfügt über zwei Transformatorimplementierungen, ein Low-Degree-Netz (f_L) und ein Excessive-Degree-Netz (f_H). Jeder Durchgang läuft wie folgt ab: f_L übernimmt die Eingabefrage und die aktuelle Antwort sowie den latenten Zustand, während f_H die Antwort basierend auf dem latenten Zustand aktualisiert. Dies ist eine Artwork Hierarchie aus schnellem „Denken“ (f_L) und langsameren „konzeptionellen“ Veränderungen (f_H). Sowohl f_L als auch f_H sind vierschichtige Transformatoren mit insgesamt ~27 Millionen Parametern.

Die HRM-Architektur trainiert unter umfassender Aufsicht: Während des Trainings führt HRM bis zu 16 aufeinanderfolgende Generations-„Verbesserungsschritte“ durch, berechnet jedes Mal einen Verlust für die Antwort und vergleicht die Steigungen aller vorherigen Schritte. Dies imitiert im Wesentlichen ein sehr tiefes Netzwerk, eliminiert jedoch die vollständige Backpropagation.

Das Modell verfügt über ein adaptives Stoppsignal (Q-Studying), das entscheidet, wann das Modell das nächste Mal trainiert und wann die Aktualisierung bei jeder Frage beendet wird. Mit dieser komplizierten Methodik schnitt HRM sehr intestine ab: Es übertraf große LLMs bei Sudoku-, Labyrinth- und ARC-AGI-Rätseln mit nur einer kleinen Stichprobe mit überwachtem Lernen.

Mit anderen Worten: HRM hat gezeigt, dass kleine Modelle mit Rekursion eine vergleichbare oder bessere Leistung erbringen können als viel größere Modelle. Der HRM-Rahmen basiert jedoch auf mehreren starken Annahmen. Seine Vorteile ergeben sich in erster Linie aus der hohen Überwachung und nicht aus dem rekursiven dualen Netzwerk.

In der Realität gibt es keine Sicherheit, dass f_L und f_H in wenigen Schritten ein Gleichgewicht erreichen. HRM verwendet außerdem eine Zwei-Netzwerk-Architektur, die auf biologischen Metaphern basiert, wodurch die Architektur schwer zu verstehen und abzustimmen ist. Schließlich erhöht das adaptive Anhalten von HRM die Trainingsgeschwindigkeit, verdoppelt jedoch die Berechnung.

Winzige rekursive Modelle (TRM): Einfachheit im Denken neu definieren

Tiny Recursive Fashions (TRMs) rationalisieren den rekursiven Prozess von HRMs und ersetzen die Hierarchie zweier Netzwerke durch ein einziges winziges Netzwerk. Bei einem vollständigen Rekursionsprozess führt ein TRM diesen Prozess iterativ durch und durchläuft die gesamte endgültige Rekursion rückwärts, ohne dass die Festkommaannahme auferlegt werden muss. Das TRM behält explizit eine vorgeschlagene Lösung 𝑦 und einen latenten Argumentationszustand 𝑧 bei und iteriert über die bloße Aktualisierung 𝑦 und des 𝑧 Argumentationszustands.

Im Gegensatz zur sequentiellen HRM-Instanz ist die vollständig kompakte Schleife in der Lage, von massiven Gewinnen bei der Generalisierung zu profitieren und gleichzeitig die Modellparameter in der TRM-Architektur zu reduzieren. Die TRM-Architektur beseitigt im Wesentlichen die Abhängigkeit von einem Fixpunkt und IFT (Implicit Mounted-Level Coaching) vollständig, da PPC (Parallel Predictive Coding) für den vollständigen Rekursionsprozess verwendet wird, genau wie HRM-Modelle. Ein einzelnes winziges Netzwerk ersetzt die beiden Netzwerke im HRM, was die Anzahl der Parameter verringert und das Risiko einer Überanpassung minimiert.

Wie TRM größere Modelle übertrifft

TRM behält zwei unterschiedliche Variablenzustände bei, die Lösungshypothese 𝑦 und die latente Gedankenkettenvariable 𝑧. Durch die Trennung von 𝑦 muss der latente Zustand 𝑧 nicht sowohl die Argumentation als auch die explizite Lösung beibehalten. Der Hauptvorteil davon besteht darin, dass die dualen Variablenzustände bedeuten, dass ein einzelnes Netzwerk beide Funktionen ausführen kann, indem es auf 𝑧 iteriert und 𝑧 in 𝑦 umwandelt, wenn sich die Eingaben nur durch die Anwesenheit oder Abwesenheit von 𝑥 unterscheiden.

Durch das Entfernen eines Netzwerks werden die Parameter im HRM halbiert Modellgenauigkeit bei Schlüsselaufgaben nimmt zu. Durch die Änderung der Architektur kann das Modell sein Lernen auf die effektive Iteration konzentrieren und die Modellkapazität reduzieren, wo Osmose überangepasst hätte. Die empirischen Ergebnisse zeigen, dass das TRM die Generalisierung mit weniger Parametern verbessert. Daher stellte das TRM fest, dass weniger Schichten eine bessere Verallgemeinerung ermöglichten als mehr Schichten. Die Reduzierung der Anzahl der Ebenen auf zwei, wobei die Rekursionsschritte proportional zur Tiefe waren, lieferte bessere Ergebnisse.

Das Modell wird umfassend überwacht, um $y$ zum Zeitpunkt des Trainings und bei jedem Schritt der Wahrheit anzupassen. Es ist so konzipiert, dass bereits ein paar Durchläufe ohne Gradienten $(y,z)$ einer Lösung näher bringen – das Erlernen der Verbesserung der Antwort erfordert additionally nur einen vollständigen Durchlauf mit Gradienten.

Vorteile von TRM

Dieses Design ist schlank und bietet viele Vorteile:

• Keine Festkomma-Annahmen: TRM eliminiert Festkommaabhängigkeiten und führt bei jeder Rekursion eine Backpropagation durch. Ausführen einer Reihe von Rekursionen ohne Gradienten.
• Einfachere latente Interpretation: TRM definiert zwei Zustandsvariablen: y (die Lösung) und z (das Gedächtnis des Denkens). Es wechselt zwischen der Verfeinerung beider, wodurch der Gedanke für einen Zweck und die Ausgabe für einen anderen Zweck erfasst wird. Die Verwendung genau dieser beiden, weder mehr noch weniger als zwei, conflict zweifellos optimum, um die Klarheit der Logik aufrechtzuerhalten und gleichzeitig die Leistung des Denkens zu steigern.
• Einzelnes Netzwerk, weniger Schichten (weniger ist mehr): Anstatt zwei Netzwerke zu verwenden, wie es das HRM-Modell mit f_L und f_H tut, komprimiert TRM alles in einem einzigen 2-Schichten-Modell. Dadurch wird die Anzahl der Parameter auf etwa 7 Millionen reduziert, eine Überanpassung vermieden und die Gesamtgenauigkeit für Sudoku von 79,5 % auf 87,4 % erhöht.
• Aufgabenspezifische Architekturen: TRM ist darauf ausgelegt, die Architektur an jede Fallaufgabe anzupassen. Anstatt zwei Netzwerke zu verwenden, wie es das HRM-Modell mit f_L und f_H tut, komprimiert TRM alles in einem einzigen 2-Schichten-Modell. Dadurch wird die Anzahl der Parameter auf etwa 7 Millionen reduziert, eine Überanpassung vermieden und die Gesamtgenauigkeit für Sudoku von 79,5 % auf 87,4 % erhöht.
• Optimierte Rekursionstiefe: TRM verwendet außerdem einen exponentiellen gleitenden Durchschnitt (EMA) für die Gewichte, um das Netzwerk zu stabilisieren. Durch die Glättung von Gewichtungen wird die Überanpassung bei kleinen Datenmengen reduziert und die Stabilität mit EMA erhöht.

Experimentelle Ergebnisse: Kleines Modell, große Wirkung

Winzige rekursive Modelle zeigen, dass kleine Modelle eine bessere Leistung erbringen können große LLMs zu einigen Denkaufgaben. Bei mehreren Aufgaben übertraf die Genauigkeit von TRM die von HRM und großen vorab trainierten Modellen:

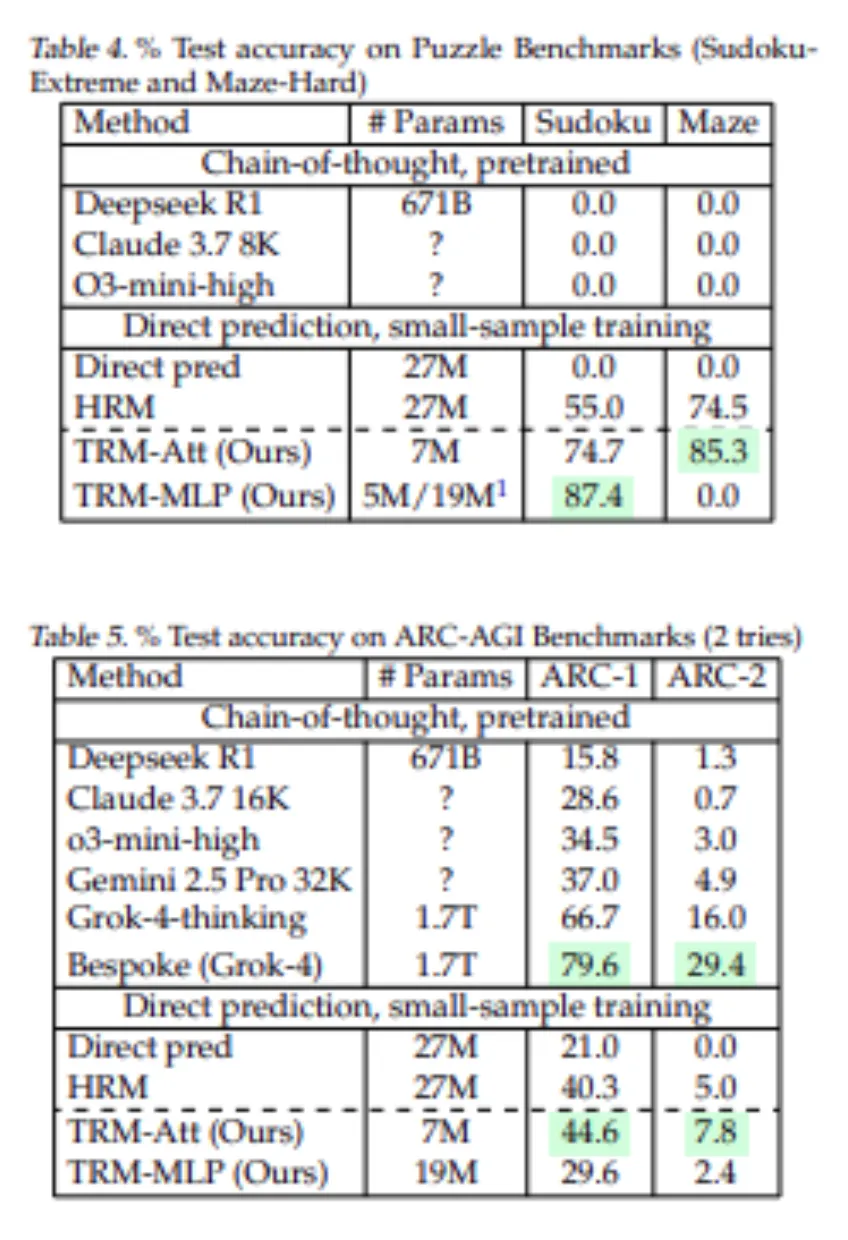
• Sudoku-Extrem: Das sind sehr schwere Sudokus. HRM (27 Millionen Parameter) ist 55,0 % genau. TRM (nur 5–7 Mio. Parameter) springt auf 87,4 (mit MLP) oder 74,7 (mit Aufmerksamkeit). Kein LLM ist überhaupt in der Nähe. Die hochmodernen Chain-of-Thought-LLMs (Deepseek R1, Claude, o3-mini) erzielten bei diesem Datensatz 0 %.
• Labyrinth-schwer: Bei Wegfindungslabyrinthen mit einer Lösungslänge > 110 ist TRM mit Aufmerksamkeit zu 85,3 % genau, während HRM zu 74,5 % genau ist. Die MLP-Model erreichte hier 0 %, was darauf hindeutet, dass Selbstaufmerksamkeit erforderlich ist. Auch hier erzielten geschulte LLMs in diesem Small-Information-Regime ~0 % auf Maze-Laborious.
• ARC-AGI-1 und ARC-AGI-2: Auf ARC-AGI-1 erreichte TRM (7M) eine Genauigkeit von 44,6 % gegenüber HRM von 40,3 %. Bei ARC-AGI-2 erzielte TRM eine Genauigkeit von 7,8 % gegenüber 5,0 % bei HRM. Beide Modelle schneiden intestine im Vergleich zu einem direkten Vorhersagemodell ab, bei dem es sich um ein 27M-Modell handelt (21,0 % auf ARC-1 und eine neue LLM-Gedankenkette, Deepseek R1 erreichte 15,8 % auf ARC-1 und 1,3 % auf ARC-2). Selbst bei intensiver Testzeitberechnung erreichte der High-LLM Gemini 2.5 Professional auf ARC-2 nur 4,9 %, während der TRM das Doppelte erreichte (praktisch keine Feinabstimmungsdaten).

Abschluss

Winzige rekursive Modelle veranschaulichen, wie Sie mit kleinen, rekursiven Architekturen erhebliche Denkfähigkeiten erreichen können. Die Komplexität wird beseitigt (dh es gibt keinen Festkomma-Trick/keine Verwendung dualer Netzwerke, keine dichten Schichten). TRM liefert genauere Ergebnisse und verwendet weniger Parameter. Es nutzt die Hälfte der Schichten und verdichtet zwei Netzwerke und verfügt nur über einige einfache Mechanismen (EMA und einen effizienteren Stoppmechanismus).

Im Wesentlichen ist TRM einfacher als HRM, lässt sich jedoch viel besser verallgemeinern. Dieses Papier zeigt das intestine gestaltete kleine Netzwerke Mit rekursivem, tiefem und überwachtem Lernen können schwierige Probleme erfolgreich gelöst werden, ohne dass eine große Größe erforderlich ist.

Dennoch stellen die Autoren einige offene Fragen zur Überlegung, zum Beispiel: Warum genau hilft Rekursion so viel mehr? Warum nicht einfach zum Beispiel ein größeres Feedforward-Netz aufbauen?

Derzeit ist TRM ein aussagekräftiges Beispiel für effiziente KI-Architekturen, da kleine Netzwerke LLMs bei Logikrätseln übertrafen und zeigt, dass beim Deep Studying manchmal weniger mehr ist.

Hallo! Ich bin Vipin, ein leidenschaftlicher Fanatic für Datenwissenschaft und maschinelles Lernen mit fundierten Kenntnissen in Datenanalyse, Algorithmen für maschinelles Lernen und Programmierung. Ich verfüge über praktische Erfahrung in der Modellerstellung, der Verwaltung unübersichtlicher Daten und der Lösung realer Probleme. Mein Ziel ist es, datengesteuerte Erkenntnisse anzuwenden, um praktische Lösungen zu schaffen, die zu Ergebnissen führen. Ich bin bestrebt, meine Fähigkeiten in einer kollaborativen Umgebung einzubringen und gleichzeitig weiterhin in den Bereichen Information Science, maschinelles Lernen und NLP zu lernen und mich weiterzuentwickeln.