Hinweis: Schauen Sie sich meine vorherigen Artikel für eine praktische Diskussion darüber, warum die Bayes’sche Modellierung für Ihre Aufgabe die richtige Wahl sein könnte.
Dieses Tutorial konzentriert sich auf einen Workflow + Code-Walkthrough zum Erstellen eines Bayesianischen Regressionsmodells in STANeine probabilistische Programmiersprache. STAN ist weit verbreitet und lässt sich mit der Sprache Ihrer Wahl verbinden (R, Python, Shell, MATLAB, Julia, Stata). Siehe die Set up führen und Dokumentation.
Ich werde verwenden Pystan für dieses Tutorial, einfach weil ich in Python programmiere. Selbst wenn Sie eine andere Sprache verwenden, unterscheiden sich die allgemeinen Bayes-Praktiken und die STAN-Sprachsyntax, die ich hier bespreche, nicht sehr.
Für den praxisorientierteren Leser gibt es hier einen Hyperlink zum Notizbuch für dieses Tutorial, Teil meines Workshops zur Bayesschen Modellierung an der Northwestern College (April 2024).
Lasst uns eintauchen!
Lernen wir, wie man ein einfaches lineares Regressionsmodell erstellt, das A und O eines jeden Statistikers, und zwar auf Bayes’sche Artwork und Weise. Unter der Annahme einer abhängigen Variable Y und Kovariate Xschlage ich das folgende einfache Modell vor:
Y = α + β * X + ϵ
Dabei ist ⍺ der Achsenabschnitt, β die Steigung und ϵ ein zufälliger Fehler. Unter der Annahme, dass
ϵ ~ Regular(0, σ)
Wir können zeigen, dass
Y ~ Regular(α + β * X, σ)
Wir lernen, wie dieses Modellformular in STAN codiert wird.
Daten generieren
Lassen Sie uns zunächst einige gefälschte Daten generieren.
#Mannequin Parameters
alpha = 4.0 #intercept
beta = 0.5 #slope
sigma = 1.0 #error-scale
#Generate pretend knowledge
x = 8 * np.random.rand(100)
y = alpha + beta * x
y = np.random.regular(y, scale=sigma) #noise
#visualize generated knowledge
plt.scatter(x, y, alpha = 0.8)
Da wir nun einige Daten zum Modellieren haben, wollen wir uns damit befassen, wie wir diese strukturieren und zusammen mit den Modellierungsanweisungen an STAN übergeben. Dies geschieht über die Modell Zeichenfolge, die normalerweise 4 (manchmal mehr) Blöcke enthält. Daten, Parameter, ModellUnd generiert MengenLassen Sie uns jeden dieser Blöcke im Element besprechen.
DATA-Block
knowledge { //enter the information to STAN
int<decrease=0> N;
vector(N) x;
vector(N) y;
}
Der Daten Block ist vielleicht der einfachste, er teilt STAN intern mit, welche Daten es erwarten soll und in welchem Format. Hier übergeben wir beispielsweise:
N: die Größe unseres Datensatzes als Typ int. Der
X: die Kovariate als Vektor der Länge N.
j: das abhängige Aspect als Vektor der Länge N.
Sehen Dokumente hier für eine vollständige Palette unterstützter Datentypen. STAN bietet Unterstützung für eine breite Palette von Typen wie Arrays, Vektoren, Matrizen usw. Wie wir oben gesehen haben, unterstützt STAN auch die Kodierung Grenzen auf Variablen. Die Kodierung von Grenzen wird empfohlen! Dies führt zu besser spezifizierten Modellen und vereinfacht die probabilistischen Sampling-Prozesse, die im Hintergrund ablaufen.
Modellblock
Als nächstes kommt der Modell Block, in dem wir STAN die Struktur unseres Modells mitteilen.
//easy mannequin block
mannequin {
//priors
alpha ~ regular(0,10);
beta ~ regular(0,1); //mannequin
y ~ regular(alpha + beta * x, sigma);
}
Der Modellblock enthält außerdem ein wichtiges und oft verwirrendes Aspect: vor Spezifikation. Prioren sind eine Quintessenz Teil der Bayes’schen Modellierung und muss für die Stichprobenaufgabe entsprechend spezifiziert werden.
Siehe meine vorherige Artikel für eine Einführung in die Rolle und Instinct hinter Vorannahmen. Zusammenfassend lässt sich sagen, vor ist eine vorausgesetzte Funktionsform für die Verteilung von Parameterwerten – oft einfach bezeichnet als vorheriger Glaube. Auch wenn Vorstrafen nicht muss genau übereinstimmen die endgültige Lösung, sie müssen es uns ermöglichen, Probe davon.
In unserem Beispiel verwenden wir Normalverteilungen mit Mittelwert 0 und unterschiedlichen Varianzen, je nachdem, wie sicher wir uns des angegebenen Mittelwerts sind: 10 für Alpha (sehr unsicher), 1 für Beta (ziemlich sicher). Hier habe ich den allgemeinen Glauben dass Alpha zwar einen weiten Bereich unterschiedlicher Werte annehmen kann, die Steigung jedoch im Allgemeinen eingeschränkter ist und keinen großen Betrag aufweist.
Daher ist im obigen Beispiel die Vorhersage für Alpha „schwächer“ als für Beta.
Wenn Modelle komplizierter werden, erweitert sich der Lösungsraum für Stichproben, und die Bereitstellung von Überzeugungen gewinnt an Bedeutung. Andernfalls ist es eine gute Praxis, wenn keine starke Instinct vorhanden ist, einfach weniger Überzeugungen in das Modell einzubringen, d. h. eine schwach informativ im Voraus und bleiben Sie flexibel gegenüber eingehenden Daten.
Die Type für y, die Sie vielleicht bereits erkannt haben, ist die Standardgleichung für lineare Regression.
Erzeugte Mengen
Zuletzt haben wir unseren Block für erzeugte Mengen. Hier teilen wir STAN mit, welche Mengen wir berechnen und als Ausgabe erhalten möchten.
generated portions { //get portions of curiosity from fitted mannequin
vector(N) yhat;
vector(N) log_lik;
for (n in 1:N) alpha + x(n) * beta, sigma);
//chance of knowledge given the mannequin and parameters
}
Hinweis: STAN unterstützt die direkte Übergabe von Vektoren in Gleichungen oder als Iterationen 1:N für jedes Aspect n. In der Praxis habe ich festgestellt, dass sich diese Unterstützung mit verschiedenen Versionen von STAN ändert. Daher ist es intestine, die iterative Deklaration auszuprobieren, wenn die vektorisierte Model nicht kompiliert werden kann.
Im obigen Beispiel-
ja: generiert Samples für y aus den angepassten Parameterwerten.
log_lik: generiert die Wahrscheinlichkeit von Daten anhand des Modells und des angepassten Parameterwerts.
Der Zweck dieser Werte wird klarer, wenn wir über die Modellbewertung sprechen.
Insgesamt haben wir nun unser erstes einfaches Bayes-Regressionsmodell vollständig spezifiziert:
mannequin = """
knowledge { //enter the information to STAN
int<decrease=0> N;
vector(N) x;
vector(N) y;
}
parameters {
actual alpha;
actual beta;
actual<decrease=0> sigma;
}mannequin {
alpha ~ regular(0,10);
beta ~ regular(0,1);
y ~ regular(alpha + beta * x, sigma);
}generated portions {
vector(N) yhat;
vector(N) log_lik;for (n in 1:N) alpha + x(n) * beta, sigma);
}
"""
Jetzt muss nur noch das Modell kompiliert und die Stichprobennahme durchgeführt werden.
#STAN takes knowledge as a dict
knowledge = {'N': len(x), 'x': x, 'y': y}
STAN nimmt Eingabedaten in Type eines Wörterbuchs entgegen. Es ist wichtig, dass dieses Wörterbuch alle Variablen enthält, die STAN laut unserer Anweisung im Modelldatenblock erwarten soll, da das Modell sonst nicht kompiliert werden kann.
#parameters for STAN becoming
chains = 2
samples = 1000
warmup = 10
# set seed
# Compile the mannequin
posterior = stan.construct(mannequin, knowledge=knowledge, random_seed = 42)
# Practice the mannequin and generate samples
match = posterior.pattern(num_chains=chains, num_samples=samples)The .pattern() technique parameters management the Hamiltonian Monte Carlo (HMC) sampling course of, the place —
- Anzahl Ketten: ist die Anzahl der Wiederholungen des Sampling-Prozesses.
- Anzahl_Beispiele: ist die Anzahl der in jeder Kette zu ziehenden Stichproben.
- sich heat laufen: ist die Anzahl der Anfangsproben, die wir verwerfen (da es einige Zeit dauert, bis die allgemeine Nähe des Lösungsraums erreicht ist).
Die Kenntnis der richtigen Werte für diese Parameter hängt sowohl von der Komplexität unseres Modells als auch von den verfügbaren Ressourcen ab.
Höhere Stichprobengrößen sind natürlich excellent, aber für ein schlecht spezifiziertes Modell erweisen sie sich als reine Zeit- und Rechenverschwendung. Ich habe schon einmal große Datenmodelle gehabt, bei denen ich eine Woche warten musste, bis sie fertig waren, nur um dann festzustellen, dass das Modell nicht konvergierte. Es ist wichtig, langsam anzufangen und Ihr Modell auf Plausibilität zu prüfen, bevor Sie eine vollwertige Stichprobennahme durchführen.
Modellbewertung
Die erzeugten Mengen werden genutzt für
- Bewertung der Anpassungsgüte, d. h. der Konvergenz,
- Vorhersagen
- Modellvergleich
Konvergenz
Der erste Schritt zur Bewertung des Modells im Bayes-Rahmen ist visuell. Wir beobachten die Stichprobenziehungen der Hamiltonsches Monte Carlo (HMC) Probenahmeverfahren.
Vereinfacht ausgedrückt, zieht STAN iterativ Stichproben für unsere Parameterwerte und wertet diese aus (HMC Weg mehr, aber das liegt außerhalb unseres derzeitigen Rahmens). Für eine gute Anpassung müssen die Stichprobenziehungen konvergieren auf einen gemeinsamen allgemeinen Bereich, der im Idealfall die globale optima.
Die obige Abbildung zeigt die Stichprobenziehungen für unser Modell über zwei unabhängige Ketten (rot und blau).
- Auf der linken Seite stellen wir die Gesamtverteilung des angepassten Parameterwertes dar, d. h. die HinterteileWir erwarten eine Regular Verteilung, wenn das Modell und seine Parameter intestine spezifiziert. (Warum ist das? Nun, eine Normalverteilung impliziert lediglich, dass es einen bestimmten Bereich von am besten passenden Werten für den Parameter gibt, was für unsere gewählte Modellform spricht). Darüber hinaus sollten wir eine beträchtliche überlappen über Ketten hinweg WENN Das Modell konvergiert zu einem Optimum.
- Auf der rechten Seite stellen wir die tatsächlichen Stichproben dar, die in jeder Iteration gezogen wurden (nur um sicherzugehen Additional sicher). Auch hier möchten wir nicht nur eine eng sondern auch eine Menge überlappen zwischen den Ziehungen.
Nicht alle Bewertungsmaßstäbe sind visuell. Gelman et al. (1) schlagen auch vor, Rhat Diagnose, die im Wesentlichen ein mathematisches Maß für die Ähnlichkeit der Stichproben zwischen den Ketten ist. Mithilfe von Rhat kann man einen Grenzwert definieren, ab dem die beiden Ketten als zu unterschiedlich beurteilt werden, um zu konvergieren. Der Grenzwert ist jedoch aufgrund der iterativen Natur des Prozesses und der variablen Aufwärmphasen schwer zu definieren.
Der visuelle Vergleich ist daher eine entscheidende Komponente, unabhängig von diagnostischen Checks
Ein häufig vorkommender Gedanke, den Sie hier haben könnten, ist: „Nun, wenn wir nur Ketten und Verteilungen haben, was ist dann der tatsächliche Parameterwert?“ Genau darum geht es. Die Bayes-Formulierung befasst sich nur mit VerteilungenNICHT Punkt Schätzungen mit ihren schwer zu interpretierenden Teststatistiken.
Dennoch kann die Posterior-Model wie folgt zusammengefasst werden: glaubwürdig Intervalle wie die Hohe Dichte Intervall (HDI), das alle x % Punkte mit der höchsten Wahrscheinlichkeitsdichte umfasst.
Es ist wichtig, Bayesianismus gegenüberzustellen glaubwürdig Intervalle mit Frequentisten Vertrauen Intervallen.
- Das glaubwürdige Intervall gibt eine Wahrscheinlichkeit Verteilung auf dem mögliche Werte für die Parameter d. h. die Wahrscheinlichkeit, dass der Parameter bei gegebenen Daten jeden Wert in einem bestimmten Intervall annimmt.
- Das Konfidenzintervall betrifft die Parameter Wert als behobenund schätzt stattdessen das Vertrauen, dass wiederholt zufällig Proben der Daten würden übereinstimmen.
Daher die
Der Bayes-Ansatz lässt die Parameterwerte fließend sein und nimmt die Daten für naked Münze, während der frequentistische Ansatz verlangt, dass es den einen wahren Parameterwert gibt … wenn wir doch nur Zugriff auf alle Daten hätten, die jemals
Puh. Lassen Sie das sacken und lesen Sie es noch einmal, bis es sackt.
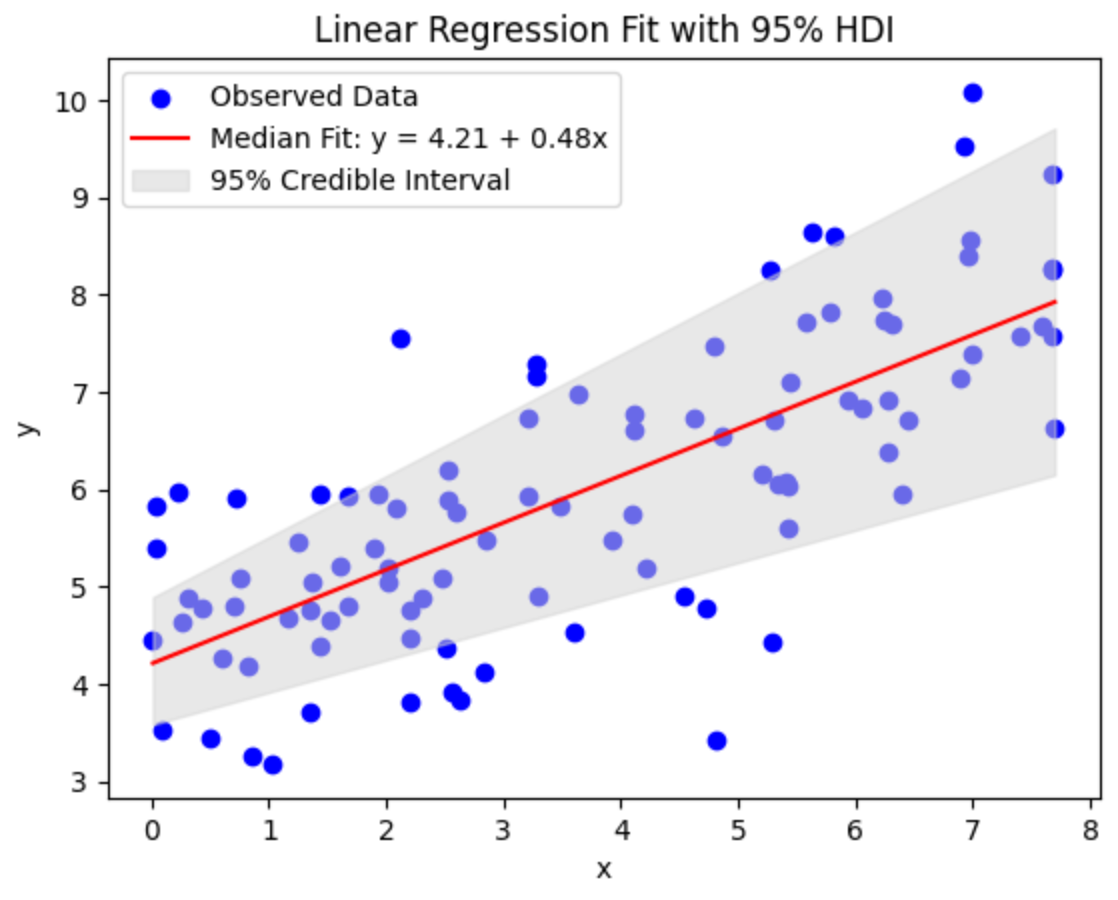
Eine weitere wichtige Folge der Verwendung glaubwürdiger Intervalle, oder anders gesagt, der Möglichkeit, den Parameter Variableist, dass die Vorhersagen, die wir machen, dies erfassen Unsicherheit mit Transparenzwobei ein bestimmter HDI-Prozentsatz die am besten passende Linie angibt.
Modellvergleich
Im Bayes’schen Rahmen wird die Watanabe-Akaike-Informationsmetrik (WAIC) Rating ist die allgemein akzeptierte Wahl für den Modellvergleich. Eine einfache Erklärung des WAIC-Scores ist, dass er das Modell schätzt Wahrscheinlichkeit während regulierend für die Anzahl der Modellparameter. Einfach ausgedrückt kann es Überanpassungen berücksichtigen. Dies ist auch ein großer Vorteil des Bayes-Frameworks – man nicht unbedingt brauchen ein Modell vorführen Validierung Datensatz. Daher
Bei knappen Daten bietet die Bayes’sche Modellierung einen entscheidenden Vorteil.
Der WAIC-Rating ist ein Vergleichend Maß, d. h. es ist nur dann von Bedeutung, wenn es zwischen verschiedenen Modellen verglichen wird, die versuchen, dieselben zugrunde liegenden Daten zu erklären. In der Praxis kann man dem Modell additionally immer mehr Komplexität hinzufügen, solange der WAIC zunimmt. Wenn der WAIC an einem Punkt in diesem Prozess der manischen Komplexitätssteigerung zu sinken beginnt, kann man Schluss machen – mehr Komplexität bietet keinen Informationsvorteil bei der Beschreibung der zugrunde liegenden Datenverteilung.
Abschluss
Zusammenfassend lässt sich sagen, dass der STAN-Modellblock einfach eine Zeichenfolge ist. Er erklärt STAN, was Sie ihm geben (Modell), was gefunden werden soll (Parameter), was Ihrer Meinung nach vor sich geht (Modell) und was es Ihnen zurückgeben soll (generierte Mengen).
Beim Einschalten dreht STAN einfach die Kurbel und gibt seine Ausgabe aus.
Die wirkliche Herausforderung besteht darin, ein geeignetes Modell zu definieren (siehe vorherige Daten), die Daten entsprechend zu strukturieren, STAN genau zu fragen, was Sie von ihm benötigen, und die Plausibilität seiner Ergebnisse zu bewerten.
Sobald wir diesen Teil verstanden haben, können wir uns mit der wahren Leistungsfähigkeit von STAN befassen, wo die Spezifikation zunehmend komplizierter Modelle zu einer einfachen syntaktischen Aufgabe wird. Tatsächlich werden wir in unserem nächsten Tutorial genau dies tun. Wir werden auf diesem einfachen Regressionsbeispiel aufbauen, um Bayesian Hierarchisch Modelle: ein Industriestandard, auf dem neuesten Stand der Technik, de facto … was auch immer. Wir werden sehen, wie wir Radom oder feste Effekte auf Gruppenebene in unsere Modelle einbauen und uns darüber wundern, wie einfach es ist, Komplexität hinzuzufügen und gleichzeitig die Vergleichbarkeit im Bayes-Rahmen aufrechtzuerhalten.
Abonnieren Sie, wenn dieser Artikel hilfreich battle, und bleiben Sie auf dem Laufenden, um mehr zu erfahren!
Verweise
(1) Andrew Gelman, John B. Carlin, Hal S. Stern, David B. Dunson, Aki Vehtari und Donald B. Rubin (2013). Bayesianische Datenanalyse, dritte Ausgabe. Chapman und Corridor/CRC.