

Bild vom Herausgeber | Midjourney
Bayesianisches Denken ist eine Methode, Entscheidungen auf der Grundlage von Wahrscheinlichkeiten zu treffen. Es beginnt mit anfänglichen Überzeugungen (Priorien) und ändert diese, wenn neue Beweise hinzukommen (Posterioren). Dies hilft dabei, bessere Vorhersagen und Entscheidungen auf der Grundlage von Daten zu treffen. Es ist von entscheidender Bedeutung in Bereichen wie KI und Statistik, in denen genaues Denken wichtig ist.
Grundlagen der Bayesschen Theorie
Schlüsselbegriffe
- Vorherige Wahrscheinlichkeit (Vorherig): Stellt die anfängliche Überzeugung bezüglich der Hypothese dar.
- Wahrscheinlichkeit: Misst, wie intestine die Hypothese die Beweise erklärt.
- Posterior-Wahrscheinlichkeit (Posterior): Kombiniert die vorherige Wahrscheinlichkeit und die Wahrscheinlichkeit.
- Beweis: Aktualisiert die Wahrscheinlichkeit der Hypothese.
Satz von Bayes
Dieser Satz beschreibt, wie die Wahrscheinlichkeit einer Hypothese auf der Grundlage neuer Informationen aktualisiert werden kann. Mathematisch ausgedrückt wird er wie folgt:
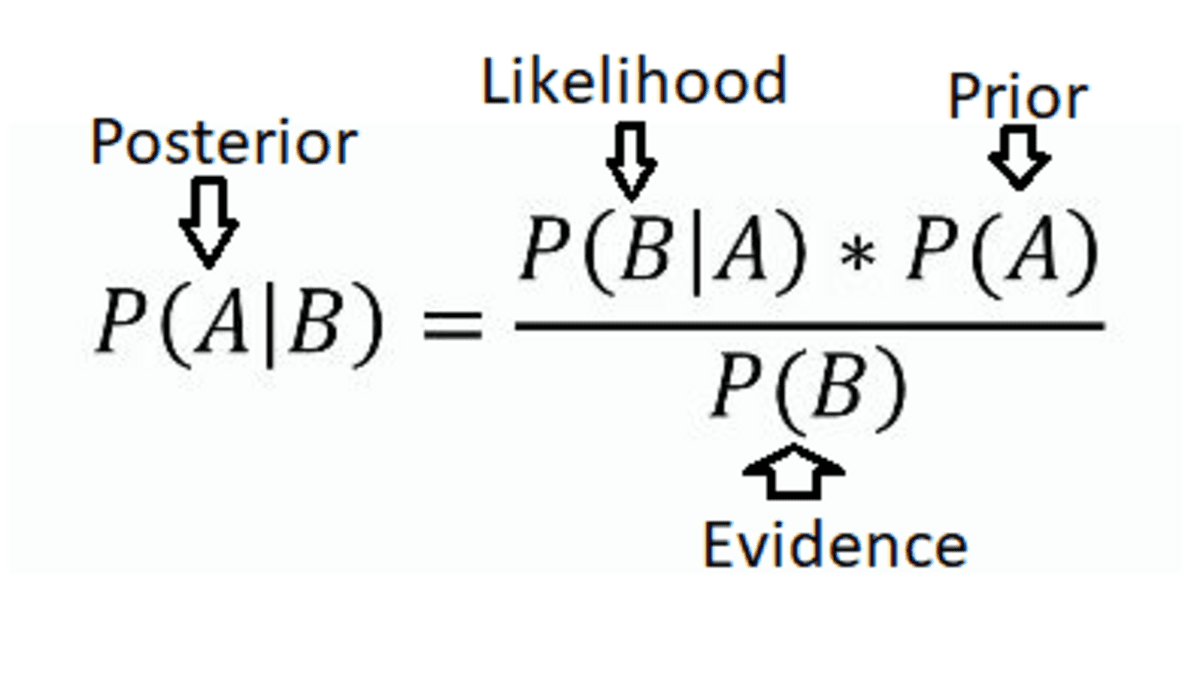
 Satz von Bayes (Quelle: Eric Castellanos Weblog)
Satz von Bayes (Quelle: Eric Castellanos Weblog)Wo:
P(A|B) ist die Posterior-Wahrscheinlichkeit der Hypothese.
P(B|A) ist die Wahrscheinlichkeit des Beweises angesichts der Hypothese.
P(A) ist die vorherige Wahrscheinlichkeit der Hypothese.
P(B) ist die Gesamtwahrscheinlichkeit des Beweises.
Anwendungen Bayesscher Methoden in der Datenwissenschaft
Bayesianische Inferenz
Die Bayessche Inferenz aktualisiert Überzeugungen, wenn Dinge unsicher sind. Sie verwendet den Satz von Bayes, um anfängliche Überzeugungen auf der Grundlage neuer Informationen anzupassen. Dieser Ansatz kombiniert das bisher Bekannte effektiv mit neuen Daten. Dieser Ansatz quantifiziert Unsicherheit und passt Wahrscheinlichkeiten entsprechend an. Auf diese Weise verbessert er kontinuierlich Vorhersagen und Verständnis, wenn mehr Beweise gesammelt werden. Er ist bei der Entscheidungsfindung nützlich, bei der Unsicherheit effektiv gemanagt werden muss.
Beispiel: Bei klinischen Studien schätzen Bayes-Methoden die Wirksamkeit neuer Behandlungen. Sie kombinieren Annahmen aus früheren Studien oder mit aktuellen Daten. Dadurch wird die Wahrscheinlichkeit aktualisiert, wie intestine die Behandlung wirkt. Forscher können dann anhand alter und neuer Informationen bessere Entscheidungen treffen.
Prädiktive Modellierung und Unsicherheitsquantifizierung
Bei prädiktiver Modellierung und Unsicherheitsquantifizierung geht es darum, Vorhersagen zu treffen und zu verstehen, wie sicher wir uns in diese Vorhersagen sind. Dabei werden Techniken wie Bayes-Methoden verwendet, um Unsicherheit zu berücksichtigen und Wahrscheinlichkeitsprognosen zu erstellen. Bayes-Modellierung ist für Vorhersagen effektiv, weil sie Unsicherheit verwaltet. Sie sagt nicht nur Ergebnisse voraus, sondern zeigt auch unser Vertrauen in diese Vorhersagen an. Dies wird durch Posterior-Verteilungen erreicht, die Unsicherheit quantifizieren.
Beispiel: Die Bayes-Regression prognostiziert Aktienkurse, indem sie eine Spanne möglicher Kurse anstelle einer einzelnen Prognose anbietet. Händler nutzen diese Spanne, um Risiken zu vermeiden und Anlageentscheidungen zu treffen.
Bayesianische neuronale Netze
Bayesianische neuronale Netzwerke (BNNs) sind neuronale Netzwerke, die probabilistische Ergebnisse liefern. Sie bieten Vorhersagen zusammen mit Unsicherheitsmaßen. Anstelle von festen Parametern verwenden BNNs Wahrscheinlichkeitsverteilungen für Gewichte und Verzerrungen. Dadurch können BNNs Unsicherheit erfassen und durch das Netzwerk verbreiten. Sie sind nützlich für Aufgaben, die Unsicherheitsmessung und Entscheidungsfindung erfordern. Sie werden bei Klassifizierung und Regression verwendet.
Beispiel: Bei der Betrugserkennung analysieren Bayes-Netze Beziehungen zwischen Variablen wie Transaktionsverlauf und Benutzerverhalten, um ungewöhnliche, mit Betrug in Zusammenhang stehende Muster zu erkennen. Sie verbessern die Genauigkeit von Betrugserkennungssystemen im Vergleich zu herkömmlichen Ansätzen.
Instruments und Bibliotheken für die Bayes-Analyse
Für die effektive Implementierung Bayesscher Methoden stehen verschiedene Instruments und Bibliotheken zur Verfügung. Lernen Sie einige beliebte Instruments kennen.
PyMC4
Es handelt sich um eine Bibliothek für probabilistische Programmierung in Python. Sie hilft bei der Bayesschen Modellierung und Inferenz. Sie baut auf den Stärken ihres Vorgängers PyMC3 auf. Durch die Integration mit JAX führt sie erhebliche Verbesserungen ein. JAX bietet automatische Differenzierung und GPU-Beschleunigung. Dadurch werden Bayessche Modelle schneller und skalierbarer.
Stan
Eine probabilistische Programmiersprache, die in C++ implementiert ist und über verschiedene Schnittstellen (RStan, PyStan, CmdStan usw.) verfügbar ist. Stan zeichnet sich durch die effiziente Durchführung von HMC- und NUTS-Sampling aus und ist für seine Geschwindigkeit und Genauigkeit bekannt. Es enthält außerdem umfangreiche Diagnosefunktionen und Instruments zur Modellprüfung.
TensorFlow-Wahrscheinlichkeit
Es handelt sich um eine Bibliothek für probabilistisches Denken und statistische Analysen in TensorFlow. TFP bietet eine Reihe von Verteilungen, Bijektoren und MCMC-Algorithmen. Die Integration mit TensorFlow gewährleistet eine effiziente Ausführung auf unterschiedlicher {Hardware}. Benutzer können damit probabilistische Modelle nahtlos mit Deep-Studying-Architekturen kombinieren. Dieser Artikel hilft bei robusten und datengesteuerten Entscheidungen.
Schauen wir uns ein Beispiel für Bayessche Statistik mit PyMC4 an. Wir werden sehen, wie man die Bayessche lineare Regression implementiert.
import pymc as pm
import numpy as np
# Generate artificial knowledge
np.random.seed(42)
X = np.linspace(0, 1, 100)
true_intercept = 1
true_slope = 2
y = true_intercept + true_slope * X + np.random.regular(scale=0.5, measurement=len(X))
# Outline the mannequin
with pm.Mannequin() as mannequin:
# Priors for unknown mannequin parameters
intercept = pm.Regular("intercept", mu=0, sigma=10)
slope = pm.Regular("slope", mu=0, sigma=10)
sigma = pm.HalfNormal("sigma", sigma=1)
# Probability (sampling distribution) of observations
mu = intercept + slope * X
probability = pm.Regular("y", mu=mu, sigma=sigma, noticed=y)
# Inference
hint = pm.pattern(2000, return_inferencedata=True)
# Summarize the outcomes
print(pm.abstract(hint))
Lassen Sie uns nun den obigen Code Schritt für Schritt verstehen.
- Es legt anfängliche Annahmen (Prioritäten) für den Achsenabschnitt, die Steigung und das Rauschen fest.
- Es definiert eine Wahrscheinlichkeitsfunktion basierend auf diesen Vorhersagen und den beobachteten Daten.
- Der Code verwendet Markov-Chain-Monte-Carlo-Sampling (MCMC), um Samples aus der Posterior-Verteilung zu generieren.
- Abschließend werden die Ergebnisse zusammengefasst, um geschätzte Parameterwerte und Unsicherheiten anzuzeigen.
Einpacken
Bayesianische Methoden kombinieren vorherige Überzeugungen mit neuen Beweisen für eine fundierte Entscheidungsfindung. Sie verbessern die Vorhersagegenauigkeit und bewältigen Unsicherheiten in mehreren Bereichen. Instruments wie PyMC4, Stan und TensorFlow Chance bieten robuste Unterstützung für die Bayesianische Analyse. Diese Instruments helfen dabei, probabilistische Vorhersagen aus komplexen Daten zu treffen.
Jayita Gulati ist eine Enthusiastin für maschinelles Lernen und technische Autorin, die von ihrer Leidenschaft für die Erstellung von Modellen für maschinelles Lernen angetrieben wird. Sie hat einen Grasp-Abschluss in Informatik von der Universität Liverpool.
