Schnell
In diesem Artikel werden wir:
1. Einführung
Modell Predictive Management (MPC) ist eine beliebte Rückkopplungsregelungsmethode, bei der ein optimales Finite-Horizon-Drawback (OCP) iterativ mit einem aktualisierten gemessenen Zustand für jede Iteration gelöst wird.

Im OCP verwendet man a Modell der Anlage, um die optimale Kontrolle der offenen Schleife über den endlichen Horizont in Betracht zu ziehen. Da das Modell das Verhalten der wahren Pflanze zu 100percentnicht erfassen kann und weil das System in der realen Welt Lärm und Störungen ausgesetzt ist, wendet man nur den ersten Teil der optimalen offenen Schleife und regelmäßig an Maßnahmen der Staat, um die OCP neu zu löschen. Dies schließt die Schleife und schafft a Rückmeldung.
Die Mathematik dahinter sind relativ einfach und intuitiv (insbesondere im Vergleich zu Dingen wie robuster Kontrolle) und es ist einfach, einen MPC -Controller zu codieren. Andere Profis sind, dass es effektiv mit harten und sanften Einschränkungen für den Staat und die Kontrolle umgehen kann (harte Einschränkungen sind streng, während weiche Einschränkungen durch Strafe der Kostenfunktion durchgesetzt werden) und kann im Allgemeinen für nichtlineare Systeme mit nicht konvexen Einschränkungen verwendet werden (je nachdem, wie böse diese natürlich sind!). Die einzige Betrügerin ist, dass Sie in Echtzeit eine Optimierungsprobleme „on-line“ lösen müssen. Dies kann ein Drawback sein, wenn Sie ein schnelles System kontrollieren oder über begrenzte Rechenressourcen verfügen.
1.2 Beispiel für laufendes Beispiel
Während des gesamten Artikels betrachte ich den Doppelintegrator mit einer Maintain-Kontrolle von Null-Ordnung (dh eine stückweise konstante Kontrolle) als das laufende Beispiel im Code. Das kontinuierliche Zeitsystem lautet:
(
start {align*}
dot x _1
mit (t in mathbb {r} ) bezeichnet die Zeit. Hier ist (x_1

Wenn wir die Steuerung auf stückweise konstante Konstant über Intervalle von 0,1 Sekunden einschränken, erhalten wir das diskrete System:
(
start {align*}
x_ {ok + 1} & = a x_k + bu_k,
finish {align*}
)
mit (ok in mathbb {z} ), wo,
(
start {align*}
A: =
hyperlinks(
start {array} {cc}
1 & 0.1
0 & 1
finish {Array}
Rechts), ,,
B: =
hyperlinks(
start {array} {c}
0.05
1
finish {Array}
Rechts)
finish {align*}
)
und (x_k in mathbb {r}^2 ), (u_k in mathbb {r} ). (Beachten Sie, dass ich (x_k ) und (u_k ) verwende, um sich auf den Zustand und die Kontrolle des diskreten Techniques zu beziehen, um den Notation im Relaxation des Artikels eingerichtet zu machen.)
Sie können die CONT2DISCRET -Funktion der Scipy -Pakete verwenden, um dieses diskrete Zeitsystem zu erhalten, wie folgt:
import numpy as np
from scipy.sign import cont2discrete
A = np.array(((0, 1),(0, 0)))
B = np.array(((0),(1)))
C = np.array(((1, 0),(0, 1)))
D = np.array(((0, 0),(0, 0)))
dt = 0.1 # in seconds
discrete_system = cont2discrete((A, B, C, D), dt, methodology='zoh')
A_discrete, B_discrete, *_ = discrete_system2. optimales Kontrollproblem
Wir werden das folgende diskrete optimale Steuerungsproblem (OCP) betrachten:
(
start {Gleichung}
{ mathhrm {OCP} ( bar x):} start {instances}
minlimits_{mathbf{u},mathbf{x}} quad & sum_{ok=0}^{Okay-1} left(x_k^{prime}Qx_k + u_k^prime R u_k proper)+ x_{Okay}^prime Q_K x_{Okay}
mathrm {Betreff TO:} quad & x_ {ok + 1} = ax_k + bu_k, & ok in (0: k-1), & dots (1)
quad & x_0 = bar x, & & Punkte (2)
quad & x_k in (-1,1) Occasions (- Infty, Infty), & ok in (1: ok), & Punkte (3)
quad & u_k in (-1,1), & ok in (0: k-1), & Punkte (4)
finish {Fälle}
finish {Gleichung}
)
Wo,
- (Okay in mathbb {r} _ { geq 0} ) bezeichnet die endlicher Horizont über das wir die OCP lösen,
- (ok in mathbb {z} ) bezeichnet den diskreten Zeitschritt,
- ((p: q) ), mit (p, q in mathbb {z} ), bezeichnet die Menge der Ganzzahlen ( {p, p+1,…, q } ),
- ( bar x in mathbb {r}^2 ) bezeichnet die Anfangsbedingung des dynamischen Techniques,
- (x_k in mathbb {r}^2 ) bezeichnet die Zustand bei Schritt (ok ),
- (u in mathbb {r} ) bezeichnet die Kontrolle bei Schritt (ok ),
- (Qinmathbb{R}^{2times 2}), (Rinmathbb{R}) and (Q_K in mathbb{R}^{2times 2}) are sq. constructive particular matrices that specify the associated fee perform ((R) is scalar right here as a result of (u ) ist skalar).
Außerdem werden wir lassen,
- ( mathbf {u}: = (u_0, u_1,…, u_ {ok – 1}) in mathbb {r}^ok ) bezeichnen die Kontrollsequenz,
- ( mathbf {x}: = (x_0, x_1,…, x_ {ok}) in mathbb {r}^{2 (ok+1)} ) Kennzeichnen Sie die Zustandssequenz.
Um streng zu sein, werden wir sagen, dass das Paar (( mathbf {u}^{*}, mathbf {x}^{*}) in mathbb {r}^ok Occasions mathbb {r}^{2 (ok+1) Occasions mathbb {r} Lösung zu ( mathhrm {OCP} ( bar {x}) ), sofern die Kostenfunktion über alle zulässigen Paare minimiert werden, dh, wie
(
start {Gleichung*}
J ( mathbf {u}^{*}, mathbf {x}^{*}) leq j ( mathbf {u}, mathbf {x}), quad forall ( mathbf {u}, mathbf {x}) in in oma
finish {Gleichung*}
)
wobei (j: mathbb {r}^ok occasions mathbb {r}^{2 (ok+1)} rightarrow mathbb {r} _ { geq 0} is,,
(
start {Gleichung*}
J(mathbf{u},mathbf{x}) :=left( sum_{ok=0}^{Okay-1 }x_k^prime Q x_k + u_k^prime R u_k proper) + x_K^prime Q_K x_K
finish {Gleichung*}
)
und ( Omega ) bezeichnet alle zulässigen Paare,
(
Omega :={(mathbf{u},mathbf{x})in mathbb{R}^{Okay}occasions mathbb{R}^{2(Okay+1)} : (1)-(4),, mathrm{maintain}}.
)
Daher besteht das optimale Kontrollproblem darin, eine Kontroll- und Statussequenz zu finden, (( mathbf {u}^{*}, mathbf {x}^{*}) ), die die Kostenfunktion minimiert, vorbehaltlich der Dynamik, (f ) sowie die Einschränkungen des Staates und Kontrolle, und Kontrolle, (x_k in (-1,1) Occasions (- inty, Infy) ), (u_k in (-1,1) ), für alle (ok ). Die Kostenfunktion ist für die Leistung des Controllers von entscheidender Bedeutung. Nicht nur im Sinne, um sicherzustellen Gleichgewichtspunkt Der geschlossene Schleifenstaat wird sich niederlassen. Mehr dazu in Abschnitt 4.
Beachten Sie, wie ( mathrm {OCP} ( bar x) ) in Bezug auf den Ausgangszustand ( bar x ) parametriert wird. Dies ergibt sich aus der grundlegenden Idee hinter MPC: dass das optimale Kontrollproblem iterativ mit einem aktualisierten gemessenen Zustand gelöst wird.
2.1 Codieren eines OCP -Lösers
Casadi Opti Stack macht es wirklich einfach, die OCP einzurichten und zu lösen.
Erstens einige Vorbereitungen:
from casadi import *
n = 2 # state dimension
m = 1 # management dimension
Okay = 100 # prediction horizon
# an arbitrary preliminary state
x_bar = np.array(((0.5),(0.5))) # 2 x 1 vector
# Linear price matrices (we'll simply use identities)
Q = np.array(((1. , 0),
(0. , 1. )))
R = np.array(((1)))
Q_K = Q
# Constraints for all ok
u_max = 1
x_1_max = 1
x_1_min = -1Jetzt definieren wir die Entscheidungsvariablen des Issues:
opti = Opti()
x_tot = opti.variable(n, Okay+1) # State trajectory
u_tot = opti.variable(m, Okay) # Management trajectoryAls nächstes stellen wir die dynamischen Einschränkungen auf und richten die Kostenfunktion ein:
# Specify the preliminary situation
opti.subject_to(x_tot(:, 0) == x_bar)
price = 0
for ok in vary(Okay):
# add dynamic constraints
x_tot_next = get_x_next_linear(x_tot(:, ok), u_tot(:, ok))
opti.subject_to(x_tot(:, ok+1) == x_tot_next)
# add to the associated fee
price += mtimes((x_tot(:,ok).T, Q, x_tot(:,ok))) +
mtimes((u_tot(:,ok).T, R, u_tot(:,ok)))
# terminal price
price += mtimes((x_tot(:,Okay).T, Q_K, x_tot(:,Okay)))def get_x_next_linear(x, u):
# Linear system
A = np.array(((1. , 0.1),
(0. , 1. )))
B = np.array(((0.005),
(0.1 )))
return mtimes(A, x) + mtimes(B, u)Der Code mtimes ((x_tot (:, ok) .t, q, x_tot (:, ok))) implementiert die Matrixmultiplikation, (x_k^{ prime} q x_k ).
Wir fügen jetzt die Kontroll- und Staatsbeschränkungen hinzu,
# constrain the management
opti.subject_to(opti.bounded(-u_max, u_tot, u_max))
# constrain the place solely
opti.subject_to(opti.bounded(x_1_min, x_tot(0,:), x_1_max))und lösen:
# Say we need to minimise the associated fee and specify the solver (ipopt)
opts = {"ipopt.print_level": 0, "print_time": 0}
opti.decrease(price)
opti.solver("ipopt", opts)
answer = opti.resolve()
# Get answer
x_opt = answer.worth(x_tot)
u_opt = answer.worth(u_tot)Wir können die Lösung mit der Funktion des Repos plot_Solution () zeichnen.
from MPC_tutorial import plot_solution
plot_solution(x_opt, u_opt.reshape(1,-1)) # should reshape u_opt to (1,Okay)
3. Modellvorhersagekontrolle
Die Lösung zu ( mathrm {ocp} ( bar x) ), (( mathbf {x}^{*}, mathbf {u}^{*}) ) für eine gegebene ( bar x ) liefert uns mit einem mit einem mit einem mit einem mit einem mit einem mit einem mit einem mit einem mit einem mit einem mit einem mit einem ein Offene Schleife Kontrolle, ( mathbf {u}^{*} ). Wir jetzt Schließen Sie die Schleife durch iteratives Lösen von ( mathrm {OCP} ( bar x) ) und Aktualisierung des Ausgangszustands (dies ist der MPC -Algorithmus).
(
start {ausgerichtet}
& textbf {enter:} quad mathbf {x}^{ mathrm {init}} in mathbb {r}^2
& quad bar x bought mathbf {x}^{ mathhrm {init}}
& textbf {für} ok in (0: infty) textbf {:}
& quad ( mathbf {x}^{*}, mathbf {u}^{*}) Get arg mathrm {OCP} ( bar x)
& quad mathrm {anwenden} u_0^{*} mathhrm { to the System}
& quad bar x gilt mathrm {gemessen state at } ok+1
& textbf {Ende für}
finish {ausgerichtet}
)
3.1 Codieren des MPC -Algorithmus
Der Relaxation ist ziemlich einfach. Zunächst werde ich alle unseren vorherigen Code in eine Funktion einfügen:
def solve_OCP(x_bar, Okay):
....
return x_opt, u_optBeachten Sie, dass ich die Funktion mit dem Ausgangszustand ( bar x ) sowie dem Vorhersagehorizont (ok ) parametriiert habe. Die MPC -Schleife wird dann implementiert mit:
x_init = np.array(((0.5),(0.5))) # 2 x 1 vector
Okay = 10
number_of_iterations = 150 # should in fact be finite!
# matrices of zeros with the right sizes to retailer the closed loop
u_cl = np.zeros((1, number_of_iterations))
x_cl = np.zeros((2, number_of_iterations + 1))
x_cl(:, 0) = x_init(:, 0)
x_bar = x_init
for i in vary(number_of_iterations):
_, u_opt = solve_OCP(x_bar, Okay)
u_opt_first_element = u_opt(0)
# save closed loop x and u
u_cl(:, i) = u_opt_first_element
x_cl(:, i+1) = np.squeeze(get_x_next_linear(x_bar,
u_opt_first_element))
# replace preliminary state
x_bar = get_x_next_linear(x_bar, u_opt_first_element)Auch hier können wir die geschlossene Schleifenlösung zeichnen.
plot_solution(x_cl, u_cl)
Beachten Sie, dass ich den Zustand der Anlage mit der Funktion get_x_next_linear () „gemessen habe“. Mit anderen Worten, ich habe angenommen, dass unser Modell zu 100% korrekt ist.
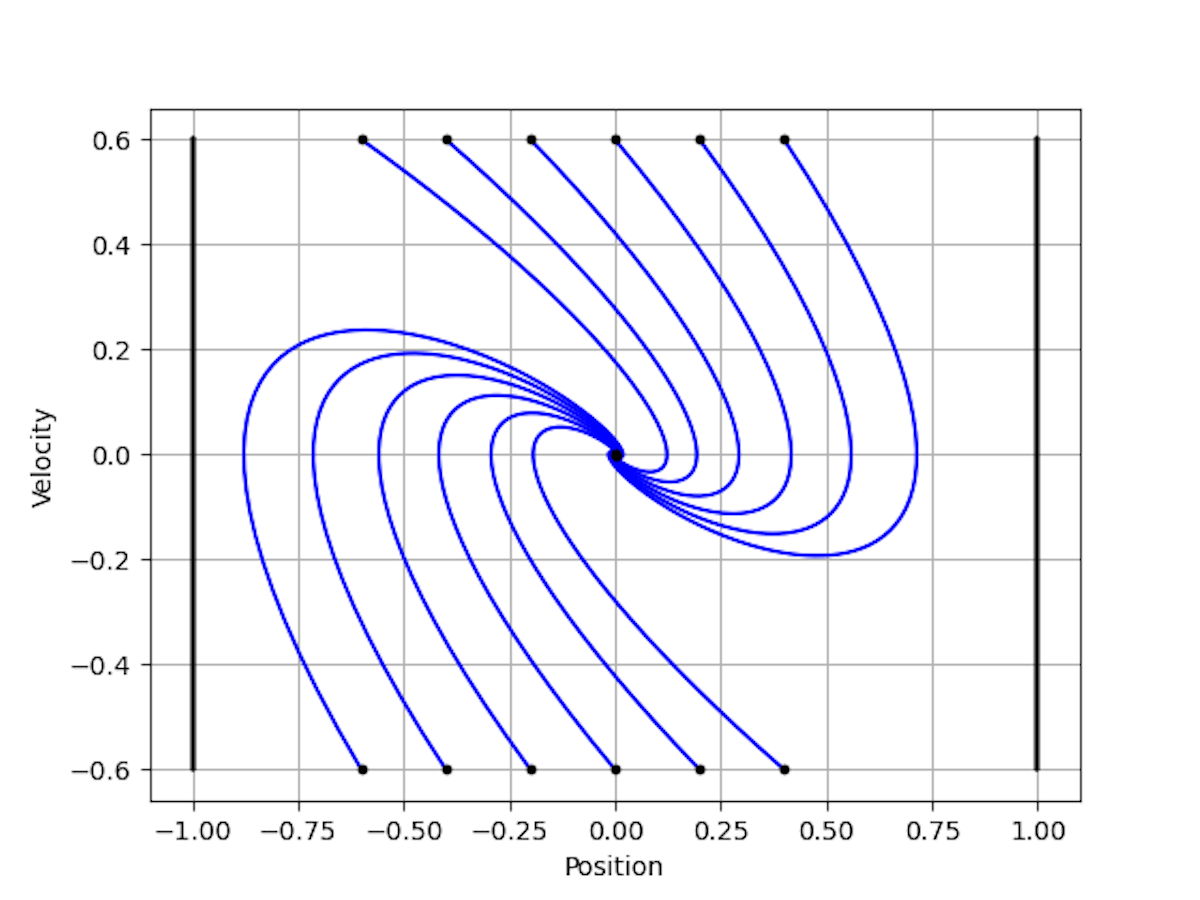
Hier ist eine Handlung der geschlossenen Schleife aus einer Reihe von Anfangszuständen.

4. Weitere Themen
4.1 Stabilität und rekursive Machbarkeit
Zwei der wichtigsten Aspekte eines MPC -Controllers sind rekursive Machbarkeit des iterativ aufgerufenen OCP und Stabilität der geschlossenen Schleife. Mit anderen Worten, wenn ich die OCP zum Zeitpunkt (ok ) gelöst habe, gibt es eine Lösung für die OCP zum Zeitpunkt (ok+1 )? Wenn es zu jedem Zeitschritt eine Lösung für den OCP gibt, wird sich der Zustand geschlossener Zustand asymptotisch an einem Gleichgewichtspunkt (dh stabil)?
Sicherstellen, dass ein MPC -Controller diese beiden Eigenschaften aufweist, beinhaltet sorgfältig die Kostenfunktion und die Einschränkungen und die Auswahl eines lang genug Vorhersagehorizonts. Wenn Sie zu unserem Beispiel zurückkehren, erinnern Sie sich daran, dass die Matrizen in der Kostenfunktion einfach ausgewählt wurden:
(
Q = hyperlinks ( start {Array} {cc}
1 & 0
0 & 1
finish {Array}
rechts), , q_k = hyperlinks ( start {array} {cc}
1 & 0
0 & 1
finish {Array}
rechts), , r = 1.
)
Mit anderen Worten, die OCP bestraft die Entfernung des Staates zum Ursprung und fährt damit dort. Wie Sie wahrscheinlich vermuten können, wenn der Vorhersagehorizont (ok ) sehr kurz ist und der Ausgangszustand sehr nahe an den Einschränkungen bei (x_1 = pm 1 ) liegt, wird der OCP Lösungen mit unzureichender „Voraussicht“ findet und das Drawback in einer zukünftigen Iteration des MPC -Schleifs unmittelbar sein. (Sie können damit auch experimentieren, indem Sie (ok ) im Code klein machen.)
4.2 einige andere Themen
MPC ist ein aktives Forschungsfeld und es gibt viele interessante Themen zu erforschen.
Was ist, wenn der vollständige Zustand nicht gemessen werden kann? Dies bezieht sich auf Beobachtbarkeit Und Ausgang MPC. Was ist, wenn mir die asymptotische Stabilität nicht wichtig ist? Dies hat (oft) mit Wirtschaftliche MPC. Wie mache ich den Controller? sturdy zu Lärm und Störungen? Es gibt ein paar Möglichkeiten, damit umzugehen, mit Rohr MPC Wahrscheinlich das bekannteste.
Zukünftige Artikel könnten sich auf einige dieser Themen konzentrieren.
5. Weiteres Lesen
Hier sind einige Customary- und sehr gute Lehrbücher auf MPC.
(1) Grüne, L. & Pannek, J. (2016). Nichtlineare Modellvorhersagekontrolle.
(2) Rawlings, JB, Mayne, DQ & Diehl, M. (2020). Modellvorhersagekontrolle: Theorie, Berechnung und Design.
(3) Kouvaritakis, B. & Cannon, M. (2016). Modellvorhersagekontrolle: klassisch, sturdy und stochastisch.