Es gibt viele gute Ressourcen, die die Transformatorarchitektur on-line erklären, aber Einbettung der Drehposition (RoPE) wird oft schlecht erklärt oder ganz übersprungen.
RoPE wurde erstmals in dem Artikel vorgestellt RoFormer: Verbesserter Transformator mit Rotationspositionseinbettungund während die beteiligten mathematischen Operationen relativ einfach sind – hauptsächlich Rotationsmatrix und Matrixmultiplikationen – liegt die eigentliche Herausforderung darin, die Instinct hinter ihrer Funktionsweise zu verstehen. Ich werde versuchen, eine Möglichkeit zu bieten, zu veranschaulichen, was es mit Vektoren macht, und zu erklären, warum dieser Ansatz so effektiv ist.
Ich gehe davon aus, dass Sie in diesem Beitrag über ein grundlegendes Verständnis von Transformatoren und dem Aufmerksamkeitsmechanismus verfügen.
RoPE-Instinct
Da es Transformatoren an inhärentem Verständnis für Ordnung und Abstände mangelt, entwickelten Forscher Positionseinbettungen. Folgendes sollten Positionseinbettungen bewirken:
- Näher beieinander liegende Token sollten eine höhere Gewichtung haben, während entfernte Token eine niedrigere Gewichtung haben sollten.
- Die Place innerhalb einer Sequenz sollte keine Rolle spielen, d. h. wenn zwei Wörter nahe beieinander liegen, sollten sie einander mit höherer Gewichtung folgen, unabhängig davon, ob sie am Anfang oder am Ende einer langen Sequenz stehen.
- Um diese Ziele zu erreichen, relative Positionseinbettungen sind weitaus nützlicher als absolute Positionseinbettungen.
Wichtige Erkenntnisse: LLMs sollten sich auf die relativen Positionen zwischen zwei Token konzentrieren, was für die Aufmerksamkeit wirklich wichtig ist.
Wenn Sie diese Konzepte verstehen, haben Sie bereits die Hälfte geschafft.
Vor RoPE
Die ursprünglichen Positionseinbettungen aus der wegweisenden Arbeit Aufmerksamkeit ist alles, was Sie brauchen wurden durch eine Gleichung in geschlossener Type definiert und dann in die semantischen Einbettungen eingefügt. Das Mischen von Positions- und Semantiksignalen im verborgenen Zustand warfare keine gute Idee. Spätere Untersuchungen bestätigten, dass LLMs Positionen eher merken (überanpassen) als verallgemeinern, was zu einer schnellen Verschlechterung führt, wenn die Sequenzlängen die Trainingsdaten überschreiten. Aber die Verwendung einer Formel in geschlossener Type macht Sinn, sie ermöglicht uns, sie auf unbestimmte Zeit zu erweitern, und RoPE macht etwas Ähnliches.
Eine Strategie, die sich im frühen Deep Studying als erfolgreich erwiesen hat, warfare: Wenn Sie nicht sicher sind, wie nützliche Funktionen für ein neuronales Netzwerk berechnet werden sollen, lassen Sie das Netzwerk diese selbst lernen! Genau das haben Modelle wie GPT-3 getan – sie haben ihre eigenen Positionseinbettungen gelernt. Die Bereitstellung von zu viel Freiheit erhöht jedoch das Risiko einer Überanpassung und führt in diesem Fall zu harten Einschränkungen für Kontextfenster (Sie können es nicht über Ihr trainiertes Kontextfenster hinaus erweitern).
Die besten Ansätze konzentrierten sich auf die Modifizierung des Aufmerksamkeitsmechanismus, sodass nahegelegene Token höhere Aufmerksamkeitsgewichtungen erhalten, während entfernte Token niedrigere Gewichtungen erhalten. Durch die Isolierung der Positionsinformationen im Aufmerksamkeitsmechanismus bleibt der verborgene Zustand erhalten und bleibt auf die Semantik fokussiert. Diese Techniken versuchten in erster Linie geschickt zu modifizieren Q Und Okay Ihre Skalarprodukte würden additionally die Nähe widerspiegeln. In vielen Artikeln wurden unterschiedliche Methoden ausprobiert, aber RoPE löste das Drawback am besten.
Rotationsintuition
RoPE ändert sich Q Und Okay durch Anwenden von Drehungen auf sie. Eine der schönsten Eigenschaften der Rotation besteht darin, dass sie Vektormodule (Größe) beibehält, die möglicherweise semantische Informationen enthalten.
Lassen q sei die Abfrageprojektion eines Tokens und okay die Schlüsselprojektion eines anderen sein. Für Token, die im Textual content nahe beieinander liegen, wird eine minimale Drehung angewendet, während weit entfernte Token größere Rotationstransformationen durchlaufen.
Stellen Sie sich zwei identische Projektionsvektoren vor – jede Drehung würde sie weiter voneinander entfernen. Genau das wollen wir.

Nun ergibt sich eine möglicherweise verwirrende Scenario: Wenn zwei Projektionsvektoren bereits weit voneinander entfernt sind, kann eine Drehung sie näher zusammenbringen. Das ist nicht was wir wollen! Sie werden gedreht, weil sie im Textual content weit entfernt sind und daher keine hohe Aufmerksamkeitsgewichtung erhalten sollten. Warum funktioniert das immer noch?
- In 2D gibt es nur eine Rotationsebene (
xy). Sie können nur im oder gegen den Uhrzeigersinn drehen.
- In 3D gibt es unendlich viele Rotationsebenen, sodass es höchst unwahrscheinlich ist, dass die Rotation zwei Vektoren näher zusammenbringt.
- Moderne Modelle arbeiten in sehr hochdimensionalen Räumen (10.000+ Dimensionen), was dies noch unwahrscheinlicher macht.
Denken Sie daran: Beim Deep Studying zählen Wahrscheinlichkeiten am meisten! Es ist akzeptabel, gelegentlich falsch zu liegen, solange die Wahrscheinlichkeiten gering sind.
Drehwinkel
Der Drehwinkel hängt von zwei Faktoren ab: m Und i. Lassen Sie uns jeden einzelnen untersuchen.
Absolute Place des Tokens m
Die Rotation nimmt mit der absoluten Place des Tokens zu m erhöht sich.
Ich weiß, was Sie denken: „m ist die absolute Place, aber haben Sie nicht gesagt, dass relative Positionen am wichtigsten sind?“
Hier liegt der Zauber: Stellen Sie sich eine 2D-Ebene vor, in der Sie einen Vektor um 𝛼 und einen anderen um β drehen. Der Winkelunterschied zwischen ihnen beträgt 𝛼-β. Die absoluten Werte von 𝛼 und β spielen keine Rolle, nur ihre Differenz. Additionally für zwei Token an Positionen m Und ndie Drehung verändert den Winkel zwischen ihnen proportional zu m-n.

Der Einfachheit halber können wir uns vorstellen, dass wir nur rotieren
q(Dies ist mathematisch korrekt, da uns die endgültigen Entfernungen und nicht die Koordinaten wichtig sind.)
Hidden-State-Index i
Anstatt eine gleichmäßige Rotation über alle Dimensionen des verborgenen Zustands hinweg anzuwenden, verarbeitet RoPE jeweils zwei Dimensionen und wendet dabei unterschiedliche Rotationswinkel auf jedes Paar an. Mit anderen Worten: Es zerlegt den langen Vektor in mehrere Paare, die in 2D um verschiedene Winkel gedreht werden können.
Wir drehen verborgene Zustandsdimensionen unterschiedlich – die Drehung ist höher, wenn i ist niedrig (Vektoranfang) und niedriger, wenn i hoch ist (Vektorende).
Diese Operation zu verstehen ist einfach, aber um zu verstehen, warum wir sie brauchen, bedarf es weiterer Erklärungen:
- Dadurch kann das Modell auswählen, was es haben soll kürzere oder längere Einflussbereiche.
- Stellen Sie sich Vektoren in 3D vor (
xyz).
- Der
xUndyAchsen repräsentieren frühe Dimensionen (niedrig).i), die eine höhere Rotation erfahren. Hauptsächlich auf projizierte TokenxUndyUm mit hoher Intensität teilnehmen zu können, muss man sehr nah dran sein.
- Der
zAchse, woiist höher, rotiert weniger. Hauptsächlich auf projizierte Tokenzkann auch aus der Ferne teilnehmen.

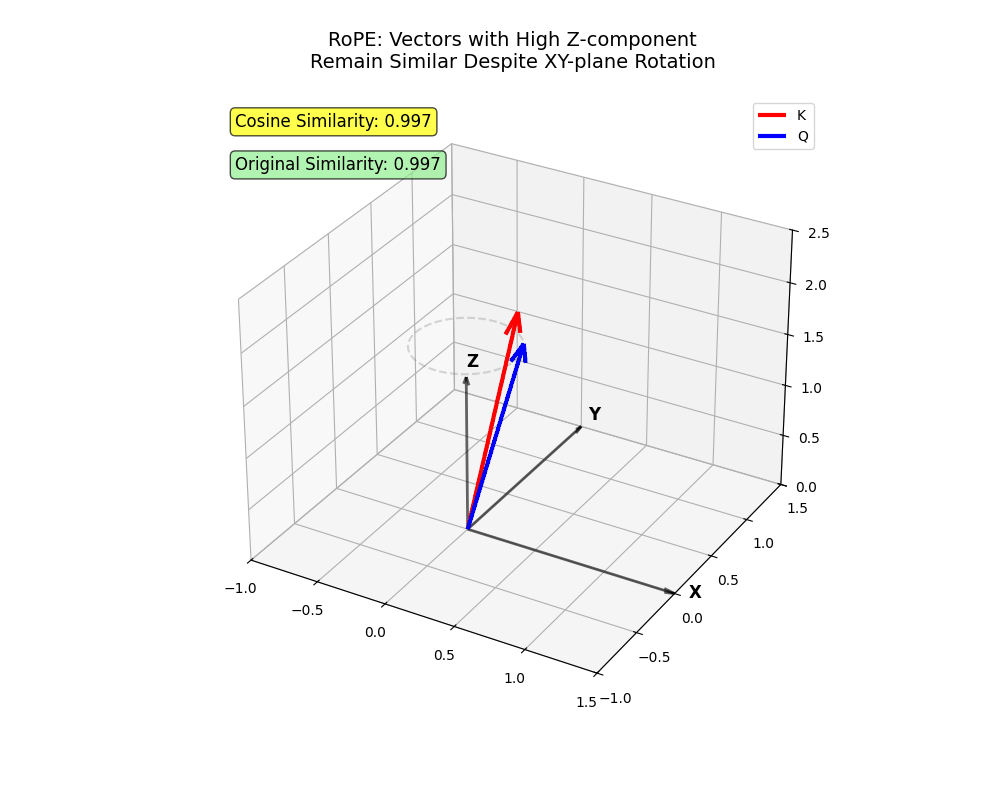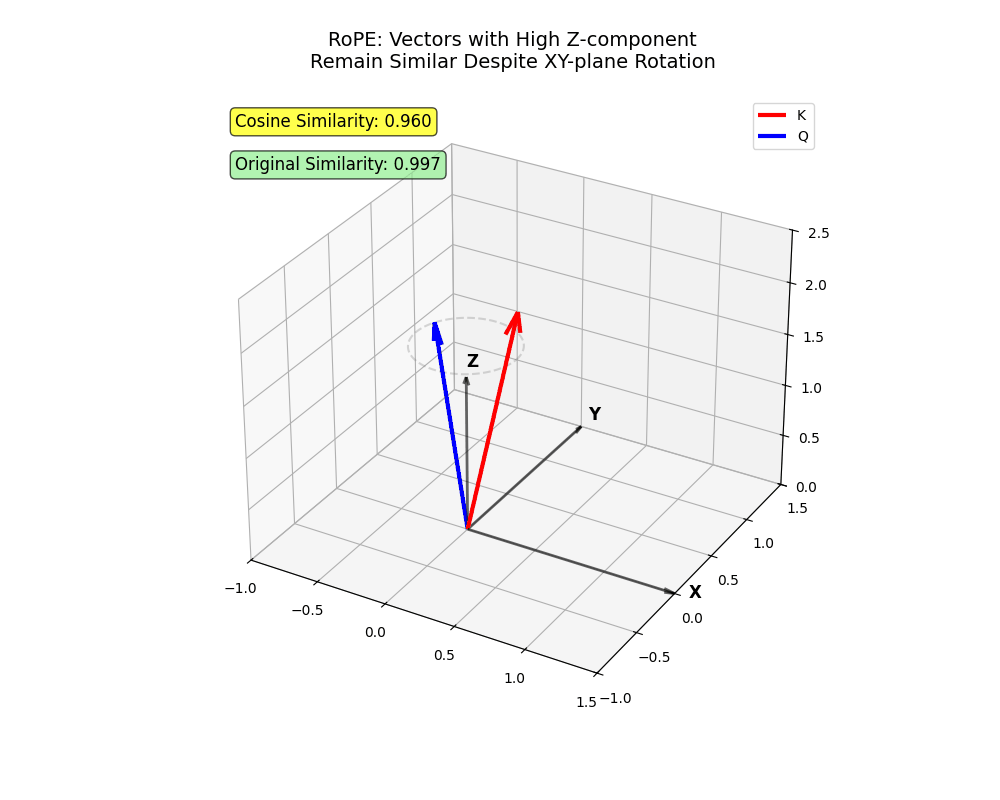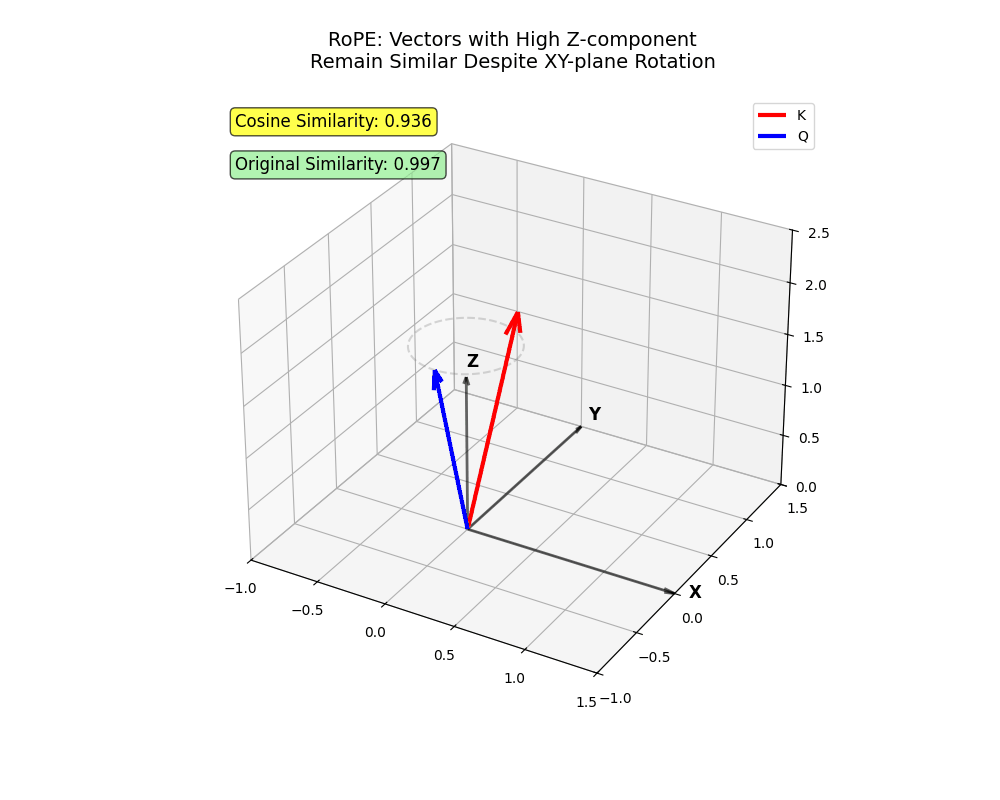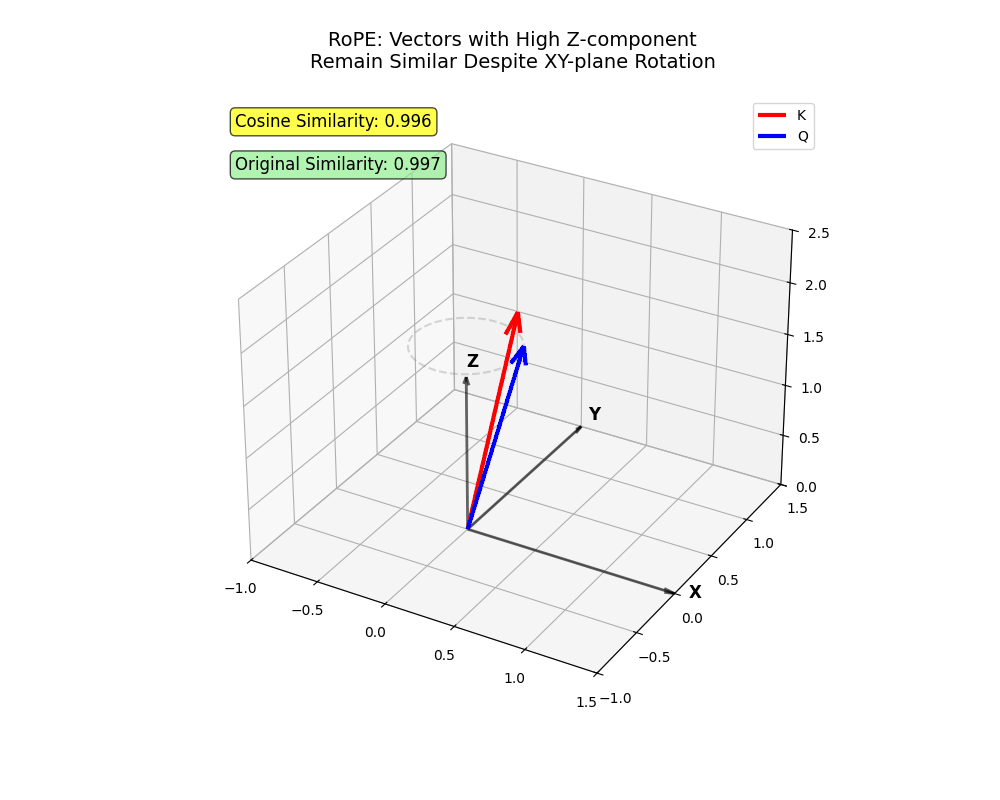
xy Flugzeug. Zwei Vektoren, die Informationen hauptsächlich in kodieren z Bleiben Sie trotz Rotation nah (Token, die trotz größerer Entfernungen anwesend sein sollten!)
x Und y sehr weit voneinander entfernt sein (in der Nähe befindliche Token, bei denen man sich nicht um den anderen kümmern sollte).Diese Struktur fängt komplizierte Nuancen der menschlichen Sprache ein – ziemlich cool, oder?
Ich weiß wieder einmal, was Sie denken: „Nach zu viel Rotation kommen sie sich wieder näher.“
Das ist richtig, aber hier ist der Grund, warum es immer noch funktioniert:
- Wir visualisieren in 3D, aber das geschieht tatsächlich in viel höheren Dimensionen.
- Während einige Dimensionen näher zusammenwachsen, wachsen andere, die langsamer rotieren, immer weiter auseinander. Daher ist es wichtig, Bemaßungen um verschiedene Winkel zu drehen.
- RoPE ist nicht perfekt – aufgrund seiner Rotationsnatur treten lokale Maxima auf. Sehen Sie sich die theoretische Tabelle der Originalautoren an:

Die theoretische Kurve weist einige verrückte Unebenheiten auf, aber in der Praxis habe ich festgestellt, dass sie sich viel besser verhält:

Mir kam die Idee, den Drehwinkel so zu beschneiden, dass die Ähnlichkeit mit zunehmendem Abstand deutlich abnimmt. Ich habe gesehen, dass Clipping auf andere Techniken angewendet wurde, nicht jedoch auf RoPE.
Bedenken Sie jedoch, dass die Kosinusähnlichkeit tendenziell zunimmt (wenn auch langsam), wenn der Abstand weit über unseren Basiswert hinaus wächst (später werden Sie genau sehen, was diese Foundation der Formel ist). Eine einfache Lösung besteht hier darin, die Foundation zu vergrößern oder sie sogar Techniken wie lokaler Aufmerksamkeit oder Fensteraufmerksamkeit zu überlassen.

Fazit: Der LLM lernt, weitreichende und kurzreichweitige Bedeutungseinflüsse in verschiedenen Dimensionen zu projizieren q Und okay.
Hier sind einige konkrete Beispiele für Abhängigkeiten mit großer und kurzer Reichweite:
- Das LLM verarbeitet Python-Code, bei dem eine anfängliche Transformation auf einen Datenrahmen angewendet wird
df. Diese relevanten Informationen sollten möglicherweise eine große Reichweite haben und die kontextuelle Einbettung nachgelagerter Prozesse beeinflussendfToken.
- Adjektive charakterisieren typischerweise nahe Substantive. In „Ein schöner Berg erstreckt sich über das Tal hinaus“, das Adjektiv Schön beschreibt speziell die Bergnicht die Schluchtes sollte sich additionally in erster Linie auf die auswirken Berg Einbettung.
Die Winkelformel
Nachdem Sie nun die Konzepte verstanden haben und eine starke Instinct haben, finden Sie hier die Gleichungen. Der Drehwinkel ist definiert durch:
(textual content{Winkel} = m instances theta)
(theta = 10.000^{-2(i-1)/d_{Modell}})
mist die absolute Place des Tokens
- i ∈ {1, 2, …, d/2} repräsentiert verborgene Zustandsdimensionen, da wir zwei Dimensionen gleichzeitig verarbeiten, zu denen wir nur iterieren müssen
d/2stattd.
d<sub>mannequin</sub>ist die verborgene Zustandsdimension (z. B. 4.096)
Beachten Sie Folgendes:
(i=1 Rightarrow theta=1 quad textual content{(hohe Rotation)} )
(i=d/2 Rightarrow theta approx 1/10.000 quad textual content{(geringe Rotation)})
Abschluss
- Wir sollten clevere Wege finden, Wissen in LLMs einzubringen, anstatt sie alles selbstständig lernen zu lassen.
- Dies erreichen wir, indem wir die richtigen Operationen bereitstellen, die ein neuronales Netzwerk zur Datenverarbeitung benötigt – Aufmerksamkeit und Faltungen sind gute Beispiele.
- Geschlossene Gleichungen können auf unbestimmte Zeit erweitert werden, da Sie nicht die Einbettung jeder Place erlernen müssen.
- Aus diesem Grund bietet RoPE eine hervorragende Flexibilität bei der Sequenzlänge.
- Die wichtigste Eigenschaft: Die Aufmerksamkeitsgewichte nehmen mit zunehmender relativer Entfernung ab.
- Dies folgt der gleichen Instinct wie die lokale Aufmerksamkeit in alternierenden Aufmerksamkeitsarchitekturen.