Ryan Socha schreibt:
In der Regel validieren oder testen wir in der statistischen Modellierung Modelle, indem wir überprüfen, wie intestine sie in einem Holdout -Datensatz funktionieren. Konzeptionell scheint es jedoch möglich, dass wir im Wesentlichen den gleichen Job machen könnten, indem wir stattdessen den Trainingsdatensatz reparieren und eine oder mehrere „Holdout -Evaluierungsfunktionen“ verwenden, die sich vom Trainingsziel unterscheiden.
Das Finden solcher Funktionen ist wahrscheinlich schwieriger als in den meisten Fällen zusätzliche Daten zu finden, aber ich bin gespannt, ob es irgendwelche Werke gibt, die Ihnen in den Sinn kommen, wenn Sie an „Holdout -Bewertungsfunktionen“ als Mittel zur Beurteilung der Modellleistung auf eine Weise denken, die nicht sein kann Goodharted.
Darüber hinaus gibt es eine allgemeinere Frage – inwieweit sind Holdout -Datensätze mit Holdout -Bewertungsfunktionen fungibel? Gibt es Fälle, in denen der Zugriff auf zusätzliche Daten einer alternativen Artwork der Bewertung der Leistung eines Modells auf den angegebenen Daten von Natur aus überlegen ist? Oder gibt es Fälle, in denen keine zusätzlichen Holdout -Daten feststellen können, dass es einen Fehler in dem, was das Modell tut?
Ich bin besonders neugierig, ob es möglicherweise ein Verfahren gibt, das von Holdout -Datensätzen in Holdout -Bewertungsfunktionen oder umgekehrt umwandeln kann. Wahrscheinlich ist eine Vorsicht erforderlich, um sicherzustellen, dass various Bewertungsfunktionen, die zum Ersetzen eines Holdout -Datensatzes erstellt wurden, keine „heimlichen“ Kopien der Holdout -Daten enthalten – aber möglicherweise ist diese Artwork des Schmuggels erforderlich, damit ein solches Verfahren überhaupt möglich ist?
Ein natürlicher Fall, in dem diese Artwork von Dingen nützlich sein könnte: Angenommen, wir möchten, dass ein Modell eine bestimmte Verteilung verallgemeinert hat, die aus den Trainingsdaten aus der Verteilung liegt, aber noch keine tatsächlichen Instanzen dieser Verteilung vorhanden sind. In solchen Fällen scheint es unsere einzige Possibility, einen Ansatz zu validieren, sicherzustellen, dass die Artwork und Weise, wie wir ihn bewerten, für die hochrangigen Eigenschaften intestine geeignet ist, von denen wir erwarten, dass sie die neue Verteilung haben. Obwohl dies einen Teil des Geschmacks der Bewertungsfunktionen zu verlieren scheint, die Holdout -Funktionen sein müssen, ist es vielleicht nicht das beste Beispiel, und dies ist nur von theoretischen Interesse.
Dies geht weit über meine Mathematik -Koteletts hinaus, alle Gedanken oder Kommentare geschätzt. Fühlen Sie sich frei, dies und jede Antwort auf Ihr Weblog zu setzen, wenn Sie der Meinung sind, dass es von Interesse wäre. Wie immer wäre es eine willkommene Antwort.
Meine Antwort: Im Laufe der Jahre haben wir viel über Kreuzvalidierung und externe Validierung nachgedacht. Zwei Schlüsselpapiere sind:
(2014) Verständnis der Vorhersageinformationskriterien für Bayes’sche Modelle. { em statistics and Computing} { bf 24}, 997–1016. (Andrew Gelman, Jessica Hwang und Aki Vehtari)
(2017) Praktische Bayes’sche Modellbewertung unter Verwendung von Depart-One-Out-Cross-Validation und Waic. { em statistics and Computing} { bf 27}, 1413–1432. (Aki Vehtari, Andrew Gelman und Jonah Gabry)
Beim Schreiben verfolgten wir den allgemeinen Development im maschinellen Lernen, der auch in Ihrer Frage ausgedrückt wurde und sich von der Betrachtung von „Informationskriterien“ als Möglichkeit zur Bewertung oder Vergleichen von Modellen und einer direkteren Interpretation von Quervalidierung als Schätzung der unter externen Validierung unter Verwendung neuer Fälle entzündeten.
Einige interessante Themen entstehen:
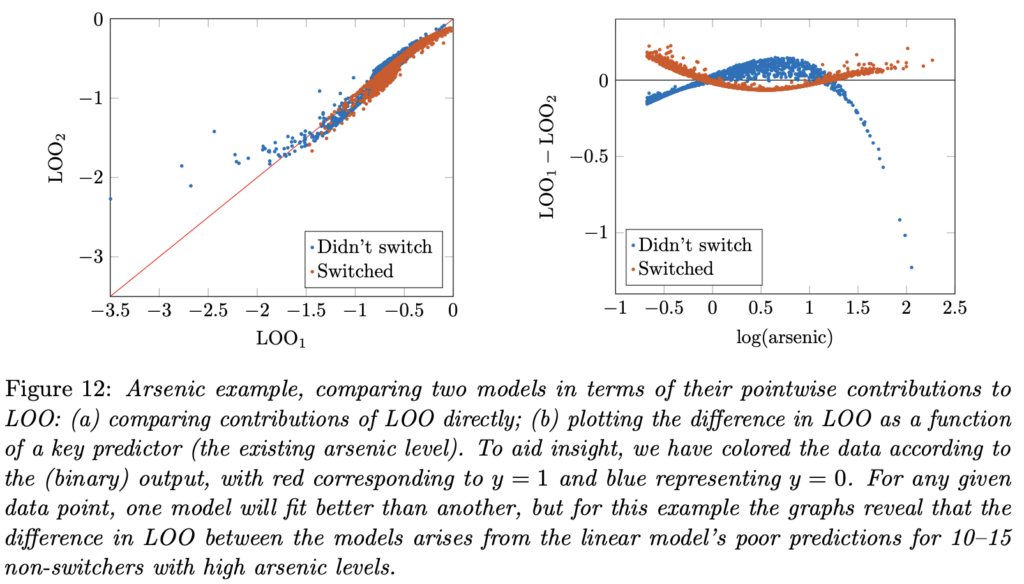
1. Wie in Ihrer Frage erwähnt, können die prädiktive Leistung in neuen Daten vom Szenario abhängen. Je weiter die neuen Daten im Prädiktorraum aus den Trainingsdaten sind, desto unsicherer und weniger genau werden Sie erwarten, dass die Vorhersagen sein. Dies deutet zunächst darauf hin, dass eine Bewertung der Vorhersageleistung eines Modells eine gewisse Spezifikation darüber erfordern sollte, wo die Bewertung durchgeführt wird, und zweitens, dass eine Kreuzvalidierung untersucht werden kann, indem Sie nicht nur die durchschnittliche Vorhersageleistung, sondern auch davon, wie die Vorhersagegenauigkeit von Prädiktoren im Modell abhängt, wie in diesem Diagramm aus unserem Artikel aus dem Jahr 2017 abhängt:

2. Die Wahl, wo Vorhersagen bewertet werden sollen und wie man diese durchschnittlich über eine zusammenfassende Maßnahme für die Vorhersagegenauigkeit erinnert, erinnert mich sehr an. . . Poststratifikation! Bei diesem ist es wichtig, Prädiktoren einzubeziehen, die die Unterschiede zwischen den Trainings- und Testdaten erfassen, und es kann sinnvoll sein, eine mehrstufige Modellierung zu verwenden, um Vorhersagen für neue Szenarien zu erleichtern. Vorhersageziele können sowohl Design als auch Analyse beeinflussen. Wenn Sie beispielsweise eine Studie mit dem Ziel durchführen, Schlussfolgerungen für zukünftige Effekte zu ziehen, kann die Zeit ein Faktor sein, und es wäre sinnvoll, Ihre Studie (Ihre Trainingsdaten) über einen bestimmten Zeitraum hinweg zu verbreiten, was Ihnen dann einen gewissen Hebel zur Schätzung von Zeittrends bei der Anpassung Ihres Modells bietet. Realistisch gesehen hängen die Schlussfolgerungen jedoch immer noch stark von Priors ab, beispielsweise wenn Sie nur eine Woche Zeit haben, um Ihr Experiment durchzuführen, aber die Effekte für ein Jahr in Zukunft schätzen möchten.
3. Die andere Sache, an die mich das erinnert, ist die Technik, die wir in letzter Zeit viel verwendet haben, eine Umfrage über sich selbst nach Strategie zu haben. Das heißt, die Daten zu nehmen, ein Modell anzupassen und dann eine aggregierte Inferenz zu erstellen, indem die Modellvorhersagen über eine hypothetische neue Inhabitants gemittelt werden, die genau in ihren Prädiktoren gleich ist wie die Daten, die zum Modell entspricht. Dies scheint eine sehr kreisförmige Sache zu sein, aber aus zwei Gründen kann es nützlich sein:
Der erste Grund dafür, dass die Nachstratifizierung einer Umfrage an sich selbst keine leere Identitätskartierung ist, ist, dass der Prozess der Anpassung des Modells als eine Glättung der Daten betrachtet werden kann, additionally kann MRP, bei dem sich Poststrat auf der Probe selbst befindet, als Dreischritt -Verfahren betrachtet werden: (i) Transformation Die Daten. (i) Inferenz kann als Inversion des angenommenen Datengeneratsprozesses angesehen werden), (iii) umgekehrte Transformation zurück zum Datenraum. Auch wenn die Schritte (i) und (iii) Umkehrungen voneinander sind, erhalten Sie etwas aus Schritt (ii). Genauso wie Sie zwei Kantenpaare auf einen Rubik’s Dice drehen können, indem Sie sich zuerst verdrehen, um die Kanten an der richtigen Stelle auszurichten, und dann den Bediener aufzutragen, der das tut, was Sie wollen, und dann Ihre ursprüngliche Wendungsmenge umzukehren.
Der zweite Vorteil einer Umfrage nach Strategie zu sich selbst besteht darin, dass Sie dies als diagnostisches Instrument nutzen können, um zu verstehen, was in einer MRP -Scenario passiert. MRP macht zwei Dinge: Sie passt an verschiedene Verteilungen von Prädiktoren in Stichprobe und Bevölkerung und glättet die Schätzung von kleiner Fläche. Wenn Sie eine Umfrage über sich selbst nachstratieren, können Sie diese beiden Dinge isolieren und nur sehen, was die Glättung tut, dann können Sie die Interessenbevölkerung nachstratieren und die Vorhersageeffekte des Ungleichgewichts bei Prädiktorverteilungen zwischen Stichprobe und Bevölkerung sehen. Wir haben diese Technik kürzlich in einem Beispiel einer Umfrage mit Messfehler verwendet, bei der wir Ergebnisse erzielten, die wir nicht verstanden haben. Die mysteriösen Muster ereigneten sich auch, als wir die Umfrage an sich selbst nachstratierten, sodass wir wussten, dass es sich nicht um ein Drawback mit einer nicht repräsentativen Stichprobe handelte. Es struggle unser Bayes’sche Modell, das schuld struggle.
4. Vor ein paar Jahren haben wir besprochen die allgegenwärtigen zweiheit der Statistiken: Die Artwork und Weise, wie klassische statistische Inferenz, Bayes’sche Statistiken und Bootstrapping alle eine Inkohärenz haben, in der zwei Modelle koexistieren, ohne dass die beiden Modelle Teil eines einzelnen konsistenten Methods sind – und wie dies tatsächlich eine gute Sache ist. Die Kreuzvalidierung oder externe Validierung hat die gleiche Eigenschaft: Es gibt das Modell, mit dem die Daten angepasst werden, und die angenommene Bevölkerung. Mathematisch können wir diese als p (y | theta, x) und p (x_new) schreiben.