Bäume sind ein beliebter beaufsichtigter Lernalgorithmus mit Vorteilen, darunter auch für Regression und Klassifizierung verwendet werden und leicht zu interpretieren sind. Entscheidungsbäume sind jedoch nicht der leistungsstärkste Algorithmus und sind aufgrund kleiner Unterschiede in den Trainingsdaten zu Überanpassung anfällig. Dies kann zu einem völlig anderen Baum führen. Aus diesem Grund wenden sich Menschen oft an Ensemble -Modelle wie gepackte Bäume und zufällige Wälder. Diese bestehen aus mehreren Entscheidungsbäumen, die auf Bootstrap -Daten geschult und aggregiert sind, um eine bessere prädiktive Leistung zu erzielen, als jeder einzelne Baum bieten könnte. Dieses Tutorial enthält Folgendes:
- Was ist einsackt
- Was macht zufällige Wälder unterschiedlich
- Coaching und Stimmen eines zufälligen Waldes mit Scikit-Study
- Berechnung und Interpretation der Merkmals Bedeutung
- Visualisieren individueller Entscheidungsbäume in einem zufälligen Wald
Wie immer ist der in diesem Tutorial verwendete Code in meinem verfügbar Github. A Videoversion Von diesem Tutorial ist auch auf meinem YouTube -Kanal für diejenigen verfügbar, die es vorziehen, visuell mitzugehen. Bemerken wir damit!
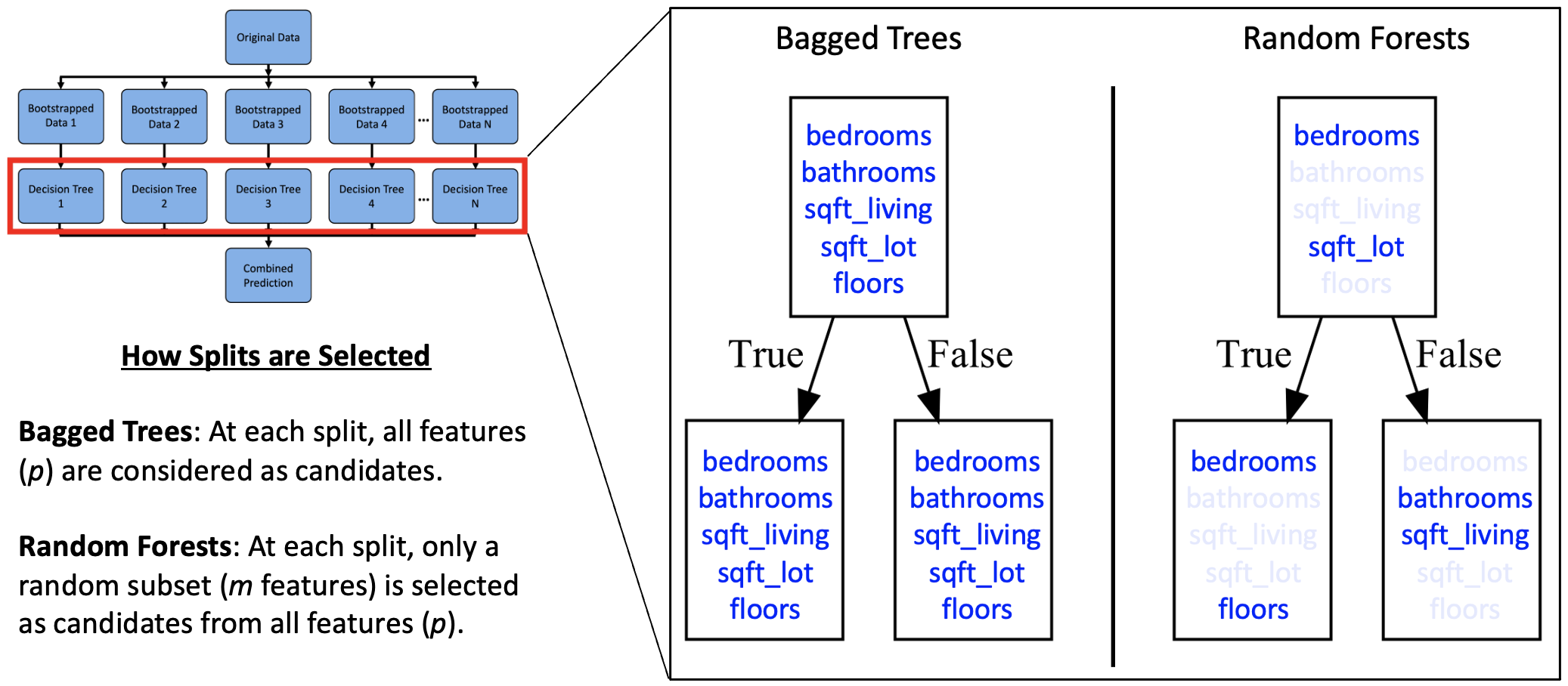
Was ist ein Sacking (Bootstrap -Aggregation)

Zufällige Wälder können als Bagging -Algorithmen eingestuft werden (BOotstrap AggRegating). Das Sacken besteht aus zwei Schritten:
1.) Bootstrap -Sampling: Erstellen Sie mehrere Trainingssätze, indem Sie Stichproben mit Ersatz aus dem ursprünglichen Datensatz zufällig zeichnen. Diese neuen Trainingseinsätze, die als Bootstrapt -Datensätze bezeichnet werden, enthalten normalerweise die gleiche Anzahl von Zeilen wie der ursprüngliche Datensatz, aber einzelne Zeilen können mehrmals oder gar nicht angezeigt werden. Im Durchschnitt enthält jeder Bootstrap -Datensatz etwa 63,2% der eindeutigen Zeilen aus den Originaldaten. Die verbleibenden ~ 36,8% der Zeilen werden ausgelassen und können für die Auswertung außerhalb des Baggage (OOB) verwendet werden. Weitere Informationen zu diesem Konzept finden Sie in meinem Probenahme mit und ohne Ersatz -Weblog -Beitrag.
2.) Aggregation Vorhersagen: Jeder Bootstrap -Datensatz wird verwendet, um ein anderes Entscheidungsbaummodell zu trainieren. Die endgültige Vorhersage erfolgt durch die Kombination der Ausgaben aller einzelnen Bäume. Für die Klassifizierung erfolgt dies normalerweise durch Mehrheitsabstimmung. Für die Regression werden Vorhersagen gemittelt.
Das Coaching jedes Baumes auf einer anderen Stiefelprobe führt zu Variationen über Bäume. Während dies die Korrelation nicht vollständig beseitigt – insbesondere wenn bestimmte Merkmale dominieren, hilft es, die Überanpassung in Kombination mit der Aggregation zu verringern. Durchschnitt der Vorhersagen vieler solcher Bäume reduziert den Gesamt Varianz des Ensembles, Verbesserung der Verallgemeinerung.
Was macht zufällige Wälder unterschiedlich

Angenommen, es gibt eine einzige starke Funktion in Ihrem Datensatz. In SackbäumeJeder Baum kann dieses Merkmal wiederholt teilen, was zu korrelierten Bäumen führt und weniger von der Aggregation profitiert. Zufällige Wälder reduzieren dieses Downside, indem sie weitere Zufälligkeit einführen. Insbesondere verändern sie, wie Spaltungen während des Trainings ausgewählt werden:
1). Erstellen Sie N -Bootstrap -Datensätze. Beachten Sie, dass das Bootstrapping in zufälligen Wäldern üblicherweise verwendet wird, es ist jedoch nicht streng erforderlich, da Schritt 2 (Auswahl der zufälligen Merkmale) eine ausreichende Vielfalt der Bäume einführt.
2). Für jeden Baum wird bei jedem Knoten eine zufällige Untergruppe von Merkmalen als Kandidaten ausgewählt, und die beste Spaltung wird aus dieser Teilmenge ausgewählt. In Scikit-Study wird dies von der gesteuert max_features Parameter, der standardmäßig angeht 'sqrt' für Klassifikatoren und 1 für Regressoren (gleichwertig mit abgesackten Bäumen).
3). Aggregation Vorhersagen: Stimmen Sie für Klassifizierung und Durchschnitt für die Regression.
Hinweis: Zufällige Wälder verwenden Probenahme mit Ersatz für Bootstrap -Datensätze und Abtastung ohne Ersatz Zur Auswahl einer Untergruppe von Funktionen.

OB-of-Bag (OOB) Rating
Da ~ 36,8% der Schulungsdaten von einem bestimmten Baum ausgeschlossen sind, können Sie diesen Holdout -Teil verwenden, um die Vorhersagen dieses Baumes zu bewerten. Scikit-Study ermöglicht dies über den Parameter OOB_SCORE = True, und bietet einen effizienten Weg, um die Verallgemeinerungsfehler abzuschätzen. Sie werden diesen Parameter im Trainingsbeispiel später im Tutorial sehen.
Coaching und Stimmen eines zufälligen Waldes in Scikit-Study
Zufällige Wälder bleiben dank ihrer Einfachheit, Interpretierbarkeit und Fähigkeit zu einer starken Grundlinie für tabellarische Daten parallelisieren Da wird jeder Baum unabhängig trainiert. Dieser Abschnitt zeigt, wie Daten geladen werden. Führen Sie einen Zugtest geteilt durchtrainieren Sie ein Basismodell, stimmen Sie Hyperparameter mit der Gittersuche ab und bewerten Sie das endgültige Modell im Testsatz.
Schritt 1: Trainieren Sie ein Basismodell
Vor dem Einstellen ist es eine gute Praxis, ein Basismodell mit angemessenen Standardeinstellungen zu trainieren. Dies gibt Ihnen ein anfängliches Leistungsgefühl und ermöglicht es Ihnen, die Generalisierung mithilfe des OB-Bag-Scores (OB-BAG) zu validieren, der in magebasierte Modelle wie zufällige Wälder integriert ist. In diesem Beispiel werden die Hausverkäufe in King County Dataset (CCO 1.0 Common Lizenz) verwendet, die zwischen Mai 2014 und Mai 2015 den Verkauf von Immobilien aus dem Gebiet von Seattle enthält. Mit diesem Ansatz können wir den Testsatz für die endgültige Bewertung nach dem Tuning reservieren.
Python"># Import libraries
# Some imports are solely used later within the tutorial
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# Dataset: Breast Most cancers Wisconsin (Diagnostic)
# Supply: UCI Machine Studying Repository
# License: CC BY 4.0
from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import RandomForestRegressor
from sklearn.inspection import permutation_importance
from sklearn.model_selection import GridSearchCV, train_test_split
from sklearn import tree
# Load dataset
# Dataset: Home Gross sales in King County (Might 2014–Might 2015)
# License CC0 1.0 Common
url = 'https://uncooked.githubusercontent.com/mGalarnyk/Tutorial_Data/grasp/King_County/kingCountyHouseData.csv'
df = pd.read_csv(url)
columns = ('bedrooms',
'loos',
'sqft_living',
'sqft_lot',
'flooring',
'waterfront',
'view',
'situation',
'grade',
'sqft_above',
'sqft_basement',
'yr_built',
'yr_renovated',
'lat',
'lengthy',
'sqft_living15',
'sqft_lot15',
'value')
df = df(columns)
# Outline options and goal
X = df.drop(columns='value')
y = df('value')
# Prepare/take a look at break up
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# Prepare baseline Random Forest
reg = RandomForestRegressor(
n_estimators=100, # variety of timber
max_features=1/3, # fraction of options thought of at every break up
oob_score=True, # permits out-of-bag analysis
random_state=0
)
reg.match(X_train, y_train)
# Consider baseline efficiency utilizing OOB rating
print(f"Baseline OOB rating: {reg.oob_score_:.3f}")
Schritt 2: Schalten Sie Hyperparameter mit der Gittersuche ab
Während das Basismodell einen starken Ausgangspunkt liefert, kann die Leistung häufig durch Tuning von Schlüsselhyperparametern verbessert werden. Grid-Suche Kreuzvalidierung, wie durch implementiert von GridSearchCVsystematisch untersucht Kombinationen von Hyperparametern und verwendet eine Kreuzvalidierung, um die einzelnen zu bewerten, wobei die Konfiguration mit der höchsten Validierungsleistung ausgewählt wird. Zu den am häufigsten abgestimmten Hyperparametern gehören:
n_estimators: Die Anzahl der Entscheidungsbäume im Wald. Mehr Bäume können die Genauigkeit verbessern, aber die Trainingszeit erhöhen.max_features: Die Anzahl der Funktionen zu berücksichtigen, wenn Sie nach dem besten Cut up suchen. Niedrigere Werte verringern die Korrelation zwischen Bäumen.max_depth: Die maximale Tiefe jedes Baumes. Flachere Bäume sind schneller, können aber unterbinden.min_samples_split: Die minimale Anzahl von Proben, die zum Aufteilen eines internen Knotens erforderlich sind. Höhere Werte können die Überanpassung verringern.min_samples_leaf: Die minimale Anzahl von Proben, die erforderlich sind, um sich an einem Blattknoten zu befinden. Hilft bei der Kontrolle der Baumgröße.bootstrap: Ob Bootstrap -Proben beim Bau von Bäumen verwendet werden. Wenn falsch, wird der gesamte Datensatz verwendet.
param_grid = {
'n_estimators': (100),
'max_features': ('sqrt', 'log2', None),
'max_depth': (None, 5, 10, 20),
'min_samples_split': (2, 5),
'min_samples_leaf': (1, 2)
}
# Initialize mannequin
rf = RandomForestRegressor(random_state=0, oob_score=True)
grid_search = GridSearchCV(
estimator=rf,
param_grid=param_grid,
cv=5, # 5-fold cross-validation
scoring='r2', # analysis metric
n_jobs=-1 # use all obtainable CPU cores
)
grid_search.match(X_train, y_train)
print(f"Finest parameters: {grid_search.best_params_}")
print(f"Finest R^2 rating: {grid_search.best_score_:.3f}")
Schritt 3: Bewerten Sie das endgültige Modell im Testsatz
Nachdem wir nun das auf Foundation von Quervalidierung basierende Modell ausgewählt haben, können wir es am Maintain-Out-Take a look at-Set bewerten, um seine Generalisierungsleistung abzuschätzen.
# Consider ultimate mannequin on take a look at set
best_model = grid_search.best_estimator_
print(f"Take a look at R^2 rating (ultimate mannequin): {best_model.rating(X_test, y_test):.3f}")
Berechnung der Wichtigkeit des zufälligen Waldmerkmals
Einer der Hauptvorteile zufälliger Wälder ist ihre Interpretierbarkeit – etwas, das große Sprachmodelle (LLMs) häufig fehlen. Während LLMs leistungsfähig sind, fungieren sie normalerweise als schwarze Kisten und können Zeigen Sie Verzerrungen auf, die schwer zu identifizieren sind. Im Gegensatz dazu unterstützt Scikit-Study zwei Hauptmethoden zur Messung der Merkmals Bedeutung in zufälligen Wäldern: mittlere Abnahme von Verunreinigungen und Permutation.
1). Durch die mittlere Verringerung der Verunreinigung (MDI): Diese Methode auch als Gini -Bedeutung bezeichnet. Diese Methode berechnet die Gesamtreduktion der Verunreinigung, die jedes Merkmal über alle Bäume übertragen wird. Dies ist schnell und in das Modell integriert über through reg.feature_importances_. Unreinheitsbasierte Merkmalsimporte können jedoch irreführend sein, insbesondere für Funktionen mit hoher Kardinalität (viele einzigartige Werte), da diese Funktionen eher ausgewählt werden, nur weil sie mehr potenzielle Cut up-Punkte liefern.
importances = reg.feature_importances_
feature_names = X.columns
sorted_idx = np.argsort(importances)(::-1)
for i in sorted_idx:
print(f"{feature_names(i)}: {importances(i):.3f}")
2). Permutation Bedeutung: Diese Methode bewertet die Abnahme der Modellleistung, wenn die Werte eines einzelnen Merkmals zufällig gemischt werden. Im Gegensatz zu MDI berücksichtigt es Function -Interaktionen und Korrelation. Es ist zuverlässiger, aber auch rechenintensiver.
# Carry out permutation significance on the take a look at set
perm_importance = permutation_importance(reg, X_test, y_test, n_repeats=10, random_state=0)
sorted_idx = perm_importance.importances_mean.argsort()(::-1)
for i in sorted_idx:
print(f"{X.columns(i)}: {perm_importance.importances_mean(i):.3f}")Es ist wichtig zu beachten, dass unsere geografischen Merkmale Lat und Lengthy auch für die Visualisierung nützlich sind, wie das folgende Diagramm zeigt. Es ist wahrscheinlich, dass Unternehmen wie Zillow die Standortinformationen in ihren Bewertungsmodellen ausgiebig einsetzen.

Visualisieren individueller Entscheidungsbäume in einem zufälligen Wald
Ein zufälliger Wald besteht aus mehreren Entscheidungsbäumen – einer für jeden über die angegebenen Schätzer n_estimators Parameter. Nach dem Coaching des Modells können Sie diese einzelnen Bäume über das Attribut .Sestimators_ zugreifen. Das Visualisieren einiger dieser Bäume kann helfen, zu veranschaulichen, wie unterschiedlich jeder die Daten aufgrund von Bootstrap -Trainingsproben und zufälligen Merkmalsauswahl bei jedem Cut up spaltet. Während das frühere Beispiel einen zufälligen ForestRegressor verwendete, zeigen wir hier diese Visualisierung anhand eines auf dem Breast Most cancers Wisconsin -Datensatzes (CC nach 4.0 -Lizenz) ausgebildeten RandomforestClassifiers, um die Vielseitigkeit von zufälligen Wäldern für Regressions- und Klassifizierungsaufgaben hervorzuheben. Dieses kurze Video zeigt, wie 100 geschulte Schätzer aus diesem Datensatz aussehen.
Passen Sie ein zufälliges Waldmodell mit Scikit-Study an
# Load the Breast Most cancers (Diagnostic) Dataset
knowledge = load_breast_cancer()
df = pd.DataFrame(knowledge.knowledge, columns=knowledge.feature_names)
df('goal') = knowledge.goal
# Organize Knowledge into Options Matrix and Goal Vector
X = df.loc(:, df.columns != 'goal')
y = df.loc(:, 'goal').values
# Cut up the information into coaching and testing units
X_train, X_test, Y_train, Y_test = train_test_split(X, y, random_state=0)
# Random Forests in `scikit-learn` (with N = 100)
rf = RandomForestClassifier(n_estimators=100,
random_state=0)
rf.match(X_train, Y_train)Zeichnen einzelner Schätzer (Entscheidungsbäume) aus einem zufälligen Wald unter Verwendung von Matplotlib
Sie können jetzt alle einzelnen Bäume aus dem montierten Modell anzeigen.
rf.estimators_

Sie können jetzt einzelne Bäume visualisieren. Der folgende Code visualisiert den ersten Entscheidungsbaum.
fn=knowledge.feature_names
cn=knowledge.target_names
fig, axes = plt.subplots(nrows = 1,ncols = 1,figsize = (4,4), dpi=800)
tree.plot_tree(rf.estimators_(0),
feature_names = fn,
class_names=cn,
stuffed = True);
fig.savefig('rf_individualtree.png')
Obwohl es schwierig zu interpretieren ist, viele Bäume zu planen, möchten Sie möglicherweise die Vielfalt zwischen den Schätzern untersuchen. Das folgende Beispiel zeigt, wie die ersten fünf Entscheidungsbäume im Wald visualisieren:
# This will likely not one of the best ways to view every estimator as it's small
fig, axes = plt.subplots(nrows=1, ncols=5, figsize=(10, 2), dpi=3000)
for index in vary(5):
tree.plot_tree(rf.estimators_(index),
feature_names=fn,
class_names=cn,
stuffed=True,
ax=axes(index))
axes(index).set_title(f'Estimator: {index}', fontsize=11)
fig.savefig('rf_5trees.png')
Abschluss
Zufällige Wälder bestehen aus mehreren Entscheidungsbäumen, die auf Bootstrap -Daten ausgebildet sind, um eine bessere prädiktive Leistung zu erzielen, als aus einer der einzelnen Entscheidungsbäume erhalten werden könnten. Wenn Sie Fragen oder Gedanken zum Tutorial haben, können Sie sich gerne durchgehen YouTube oder X.