Deep-Studying-Modelle basieren auf Aktivierungsfunktionen, die Nichtlinearität bieten und es Netzwerken ermöglichen, komplizierte Muster zu lernen. In diesem Artikel wird die Softplus-Aktivierungsfunktion erläutert, was sie ist und wie sie in PyTorch verwendet werden kann. Man kann sagen, dass Softplus eine reibungslose Type der beliebten ReLU-Aktivierung ist, die die Nachteile von ReLU abmildert, aber auch ihre eigenen Nachteile mit sich bringt. Wir werden besprechen, was Softplus ist, seine mathematische Formel, seinen Vergleich mit ReLU, seine Vorteile und Einschränkungen und einen Spaziergang durch PyTorch-Code machen, der es verwendet.
Was ist die Softplus-Aktivierungsfunktion?
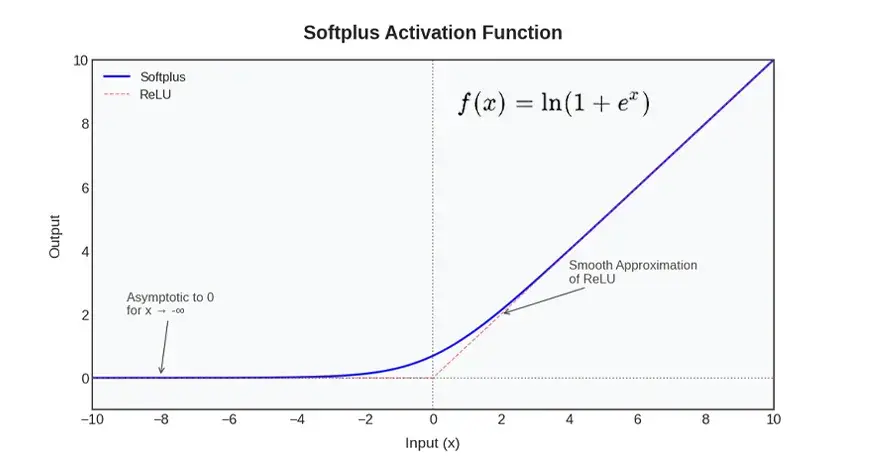
Die Softplus-Aktivierungsfunktion ist eine nichtlineare Funktion neuronaler Netze und zeichnet sich durch eine glatte Annäherung an die ReLU-Funktion aus. Einfacher ausgedrückt verhält sich Softplus wie ReLU in Fällen, in denen die optimistic oder destructive Eingabe sehr groß ist, aber eine scharfe Ecke am Nullpunkt fehlt. Stattdessen steigt es sanft an und führt zu einem marginalen positiven Output gegenüber negativen Inputs statt einer festen Null. Dieses kontinuierliche und differenzierbare Verhalten impliziert, dass Softplus überall kontinuierlich und differenzierbar ist, im Gegensatz zu ReLU, das bei x = 0 diskontinuierlich (mit einer starken Änderung der Steigung) ist.
Warum wird Softplus verwendet?
Softplus wird von Entwicklern ausgewählt, die eine bequemere Aktivierung bevorzugen. Gradienten ungleich Null, auch wenn ReLU sonst inaktiv wäre. Bei der Gradienten-basierten Optimierung können größere Störungen durch die Sanftheit von Softplus (der Gradient verschiebt sich sanft statt schrittweise) vermieden werden. Außerdem werden Ausgänge von Natur aus beschnitten (wie es bei ReLU der Fall ist), die Beschneidung ist jedoch nicht auf Null. Zusammenfassend ist Softplus die weichere Model von ReLU: Es ist ReLU-ähnlich, wenn der Wert groß ist, liegt aber besser bei Null und ist schön glatt.
Mathematische Softplus-Formel
Der Softplus ist mathematisch definiert als:
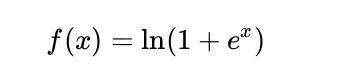
Wann X ist groß, eX ist sehr groß und daher ln(1 + eX) ist sehr ähnlich ln(zX)gleich X. Dies impliziert, dass Softplus bei großen Eingaben nahezu linear ist, z ReLU.
Wann X ist groß und negativ, eX ist additionally sehr klein ln(1 + eX) ist quick ln(1)und dieser ist 0. Die von Softplus erzeugten Werte liegen nahe bei Null, aber niemals bei Null. Um einen Wert von Null anzunehmen, muss x sich der negativen Unendlichkeit nähern.
Praktisch ist auch, dass die Ableitung von Softplus das Sigmoid ist. Die Ableitung von ln(1 + eX) Ist:
eX / (1 + eX)
Dies ist das eigentliche Sigmoid von X. Dies impliziert, dass die Steigung von Softplus zu jedem Zeitpunkt gleich ist Sigmoid(x)Das heißt, es hat überall einen Gradienten ungleich Null und ist glatt. Dies macht Softplus für das farbverlaufsbasierte Lernen nützlich, da es keine flachen Bereiche gibt, in denen die Farbverläufe verschwinden.
Verwendung von Softplus in PyTorch
PyTorch stellt die Aktivierung Softplus als native Aktivierung bereit und kann somit problemlos wie ReLU oder jede andere Aktivierung verwendet werden. Ein Beispiel für zwei einfache ist unten aufgeführt. Ersteres verwendet Softplus für eine kleine Anzahl von Testwerten, und letzteres zeigt, wie Softplus in eine kleine Anzahl eingefügt wird neuronales Netzwerk.
Softplus zu Beispieleingaben
Es gilt der folgende Ausschnitt nn.Softplus zu einem kleinen Tensor, damit Sie sehen können, wie er sich bei negativen, Null- und positiven Eingaben verhält.
import torch
import torch.nn as nn
# Create the Softplus activation
softplus = nn.Softplus() # default beta=1, threshold=20
# Pattern inputs
x = torch.tensor((-2.0, -1.0, 0.0, 1.0, 2.0))
y = softplus(x)
print("Enter:", x.tolist())
print("Softplus output:", y.tolist())
Was das zeigt:
- Bei x = -2 und x = -1 besteht der Wert von Softplus aus kleinen positiven Werten und nicht aus 0.
- Die Ausgabe beträgt ungefähr 0,6931 bei x = 0, d. h ln(2)
- Bei positiven Eingaben wie 1 oder 2 sind die Ergebnisse etwas größer als die Eingaben, da Softplus die Kurve glättet. Softplus nähert sich mit steigender Zahl x an.
Das Softplus von PyTorch wird durch die Formel dargestellt ln(1 + exp(betax)). Sein interner Schwellenwert von 20 soll einen numerischen Überlauf verhindern. Softplus ist im großen Betatakt linear, was bedeutet, dass PyTorch in diesem Fall einfach zurückkehrt X.
Verwendung von Softplus in einem neuronalen Netzwerk
Hier ist ein einfaches PyTorch-Netzwerk, das Softplus als Aktivierung für seine verborgene Schicht verwendet.
import torch
import torch.nn as nn
class SimpleNet(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
tremendous(SimpleNet, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.activation = nn.Softplus()
self.fc2 = nn.Linear(hidden_size, output_size)
def ahead(self, x):
x = self.fc1(x)
x = self.activation(x) # apply Softplus
x = self.fc2(x)
return x
# Create the mannequin
mannequin = SimpleNet(input_size=4, hidden_size=3, output_size=1)
print(mannequin)
Das Weiterleiten einer Eingabe durch das Modell funktioniert wie gewohnt:
x_input = torch.randn(2, 4) # batch of two samples
y_output = mannequin(x_input)
print("Enter:n", x_input)
print("Output:n", y_output)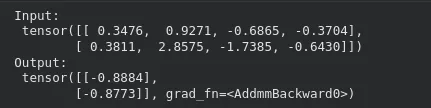
In dieser Anordnung wird die Softplus-Aktivierung verwendet, sodass die in der ersten Schicht an die zweite Schicht übergebenen Werte nicht negativ sind. Der Ersatz von Softplus durch ein bestehendes Modell erfordert möglicherweise keine weiteren strukturellen Änderungen. Es ist nur wichtig zu bedenken, dass Softplus beim Coaching möglicherweise etwas langsamer ist und mehr Rechenleistung erfordert als ReLU.
Die letzte Ebene kann auch mit Softplus implementiert werden, wenn es optimistic Werte gibt, die ein Modell als Ausgaben generieren soll, z. B. Skalenparameter oder optimistic Regressionsziele.
Softplus vs. ReLU: Vergleichstabelle
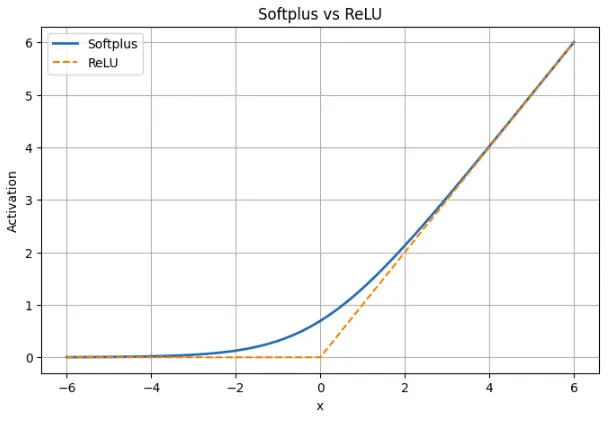
| Aspekt | Softplus | ReLU |
|---|---|---|
| Definition | f(x) = ln(1 + eX) | f(x) = max(0, x) |
| Type | Glatter Übergang über alle x | Scharfer Knick bei x = 0 |
| Verhalten für x < 0 | Kleine optimistic Ausgabe; erreicht nie Null | Die Ausgabe ist genau Null |
| Beispiel bei x = -2 | Softplus ≈ 0,13 | ReLU = 0 |
| Nahe x = 0 | Glatt und differenzierbar; Wert ≈ 0,693 | Bei 0 nicht differenzierbar |
| Verhalten für x > 0 | Quick linear, entspricht weitgehend ReLU | Linear mit Steigung 1 |
| Beispiel bei x = 5 | Softplus ≈ 5,0067 | ReLU = 5 |
| Gradient | Immer ungleich Null; Ableitung ist Sigmoid(x) | Null für x < 0, undefiniert bei 0 |
| Gefahr toter Neuronen | Keiner | Bei negativen Eingaben möglich |
| Sparsamkeit | Erzeugt keine exakten Nullen | Erzeugt echte Nullen |
| Trainingseffekt | Stabiler Farbverlauf, reibungslosere Aktualisierungen | Einfach, kann aber bei manchen Neuronen zu Lernstörungen führen |
Ein Analogon von ReLU ist Softplus. Es handelt sich um ReLU mit sehr großen positiven oder negativen Eingaben, bei dem jedoch die Ecke bei Null entfernt wurde. Dies verhindert tote Neuronen, da der Gradient nicht auf Null geht. Dies hat den Preis, dass Softplus keine echten Nullen generiert, was bedeutet, dass es nicht so spärlich ist wie ReLU. Softplus sorgt für eine komfortablere Trainingsdynamik in der Praxis, ReLU wird jedoch weiterhin verwendet, da es schneller und einfacher ist.
Vorteile der Verwendung von Softplus
Softplus bietet einige praktische Vorteile, die es bei einigen Modellen nützlich machen.
- Überall glatt und differenzierbar
Bei Softplus gibt es keine scharfen Ecken. Es ist für jede Eingabe völlig differenzierbar. Dies hilft bei der Aufrechterhaltung von Gradienten, was letztendlich die Optimierung etwas einfacher machen kann, da der Verlust langsamer variiert.
- Vermeidet tote Neuronen
ReLU kann die Aktualisierung verhindern, wenn ein Neuron kontinuierlich destructive Eingaben erhält, da der Gradient Null ist. Softplus gibt bei negativen Zahlen nicht den genauen Nullwert an und daher bleiben alle Neuronen teilweise aktiv und werden im Gradienten aktualisiert.
- Reagiert positiver auf destructive Eingaben
Softplus verwirft die negativen Eingaben nicht, indem es wie ReLU einen Nullwert generiert, sondern generiert einen kleinen positiven Wert. Dadurch kann das Modell einen Teil der Informationen über destructive Signale behalten, anstatt sie vollständig zu verlieren.
Kurz gesagt: Softplus sorgt für den Fluss von Gradienten, verhindert tote Neuronen und bietet ein reibungsloses Verhalten für den Einsatz in einigen Architekturen oder Aufgaben, bei denen Kontinuität wichtig ist.
Einschränkungen und Kompromisse von Softplus
Es gibt auch Nachteile von Softplus, die die Häufigkeit seiner Nutzung einschränken.
- Teurer in der Berechnung
Softplus verwendet exponentielle und logarithmische Operationen, die langsamer sind als die einfachen max(0, x) von ReLU. Dieser zusätzliche Overhead ist bei großen Modellen deutlich spürbar, da ReLU auf der meisten {Hardware} extrem optimiert ist.
- Keine echte Sparsamkeit
ReLU generiert perfekte Nullen für destructive Beispiele, was Rechenzeit sparen und gelegentlich bei der Regularisierung helfen kann. Softplus gibt keine echte Null an und daher sind nicht immer alle Neuronen inaktiv. Dadurch wird das Risiko toter Neuronen eliminiert und die Effizienzvorteile spärlicher Aktivierungen genutzt.
- Verlangsamen Sie schrittweise die Konvergenz tiefer Netzwerke
ReLU wird häufig zum Trainieren tiefer Modelle verwendet. Es weist einen scharfen Cutoff und einen linearen positiven Bereich auf, der das Lernen erzwingen kann. Softplus ist flüssiger und kann insbesondere in sehr tiefen Netzwerken, in denen der Unterschied zwischen den Schichten gering ist, zu langsamen Aktualisierungen führen.
Zusammenfassend lässt sich sagen, dass Softplus über nette mathematische Eigenschaften verfügt und Probleme wie tote Neuronen vermeidet. Diese Vorteile führen jedoch nicht immer zu besseren Ergebnissen in tiefen Netzwerken. Es wird am besten in Fällen verwendet, in denen Glätte oder optimistic Ergebnisse wichtig sind, und nicht als universeller Ersatz für ReLU.
Abschluss
Softplus bietet reibungslose, weiche Alternativen von ReLU zu den neuronalen Netzen. Es lernt Gradienten, tötet keine Neuronen ab und ist über alle Eingaben hinweg vollständig differenzierbar. Bei großen Werten verhält es sich wie ReLU, verhält sich jedoch bei Null eher wie eine Konstante als ReLU, da es eine Ausgabe und eine Steigung ungleich Null erzeugt. Mittlerweile ist es mit Kompromissen verbunden. Die Berechnung ist auch langsamer; Es generiert auch keine echten Nullen und beschleunigt das Lernen in tiefen Netzwerken möglicherweise nicht so schnell wie ReLU. Softplus ist in Modellen effektiver, in denen die Steigungen glatt sind oder in denen optimistic Ausgaben obligatorisch sind. In den meisten anderen Szenarien ist es eine nützliche Various zu einem Standardersatz von ReLU.
Häufig gestellte Fragen
A. Softplus verhindert tote Neuronen, indem es die Gradienten für alle Eingaben ungleich Null hält. Dies bietet eine reibungslose Various zu ReLU und verhält sich bei großen positiven Werten dennoch ähnlich.
A. Dies ist eine gute Wahl, wenn Ihr Modell von glatten Verläufen profitiert oder streng optimistic Werte ausgeben muss, wie z. B. Skalierungsparameter oder bestimmte Regressionsziele.
A: Es ist langsamer zu berechnen als ReLU, erzeugt keine spärlichen Aktivierungen und kann in tiefen Netzwerken zu einer etwas langsameren Konvergenz führen.
Melden Sie sich an, um weiterzulesen und von Experten kuratierte Inhalte zu genießen.