Ich habe bereits darüber geschrieben, wie sehr mir Andrew Ngs Coursera-Kurs zum maschinellen Lernen gefallen hat. Allerdings habe ich auch erwähnt, dass der Kurs meiner Meinung nach im Bereich Empfehlungssysteme ein paar Schwächen aufweist. Nach dem Erlernen grundlegender Modelle für Regression und Klassifizierung vervollständigen Empfehlungssysteme wahrscheinlich das Triumvirat der Säulen des maschinellen Lernens für die Datenwissenschaft.
Da ich bei einem E-Commerce-Unternehmen arbeite, denke ich viel über Empfehlungssysteme nach und möchte eine Einführung in grundlegende Empfehlungsmodelle geben. Das Ziel eines Empfehlungsmodells besteht darin, bei einem bestimmten Eingabeobjekt eine Rangliste von Objekten zu präsentieren. Normalerweise basiert diese Rangfolge auf der Ähnlichkeit zwischen dem Eingabeobjekt und den aufgelisteten Objekten. Um es weniger vage auszudrücken: Man möchte oft entweder ähnliche Produkte zu einem bestimmten Produkt präsentieren oder Produkte präsentieren, die einem bestimmten Benutzer persönlich empfohlen werden.
Das Erstaunliche dabei ist, dass, wenn man über genügend Benutzer-Produktdaten (Bewertungen, Käufe usw.) verfügt, keine weiteren Informationen erforderlich sind, um vernünftige Empfehlungen abzugeben. Dies unterscheidet sich deutlich von Regressions- und Klassifizierungsproblemen, bei denen man verschiedene Merkmale untersuchen muss, um die Vorhersagekraft eines Modells zu verbessern.
Für diese Einführung verwende ich den MovieLens-Datensatz – einen klassischen Datensatz zum Trainieren von Empfehlungsmodellen. Er ist von der GroupLens-Web site erhältlich. Es gibt verschiedene Datensätze, aber der, den ich unten verwenden werde, besteht aus 100.000 Filmbewertungen von Benutzern (auf einer Skala von 1 bis 5). Die Hauptdatendatei besteht aus einer tabulatorgetrennten Liste mit Benutzer-ID (beginnend bei 1), Artikel-ID (beginnend bei 1), Bewertung und Zeitstempel als den vier Feldern. Wir können Bash-Befehle im Jupyter-Pocket book verwenden, um die Datei herunterzuladen und sie dann mit Pandas einzulesen.
import numpy as np
import pandas as pd
# !curl -O http://recordsdata.grouplens.org/datasets/movielens/ml-100k.zip
# !unzip ml-100k.zip
(0m(01;32mallbut.pl(0m* u1.base u3.base u5.base ub.base u.data
grid_search.cpkl u1.check u3.check u5.check ub.check u.merchandise
(01;32mmku.sh(0m* u2.base u4.base ua.base u.knowledge u.occupation
README u2.check u4.check ua.check u.style u.person
!head u.knowledge
!echo # line break
!wc -l u.knowledge
196 242 3 881250949
186 302 3 891717742
22 377 1 878887116
244 51 2 880606923
166 346 1 886397596
298 474 4 884182806
115 265 2 881171488
253 465 5 891628467
305 451 3 886324817
6 86 3 883603013
100000 u.knowledge
names = ('user_id', 'item_id', 'ranking', 'timestamp')
df = pd.read_csv('u.knowledge', sep='t', names=names)
df.head()
| Benutzer-ID | Artikel Identifikationsnummer | Bewertung | Zeitstempel | |
|---|---|---|---|---|
| 0 | 196 | 242 | 3 | 881250949 |
| 1 | 186 | 302 | 3 | 891717742 |
| 2 | 22 | 377 | 1 | 878887116 |
| 3 | 244 | 51 | 2 | 880606923 |
| 4 | 166 | 346 | 1 | 886397596 |
n_users = df.user_id.distinctive().form(0)
n_items = df.item_id.distinctive().form(0)
print str(n_users) + ' customers'
print str(n_items) + ' gadgets'
943 customers
1682 gadgets
Die meisten Empfehlungsmodelle bestehen aus der Erstellung einer Benutzer-für-Artikel-Matrix mit einer Artwork „Interaktions“-Nummer in jeder Zelle. Wenn man die numerischen Bewertungen einbezieht, die Benutzer den Artikeln geben, dann nennt man das eine explizites Suggestions Modell. Alternativ kann man einschließen implizites Suggestions Dabei handelt es sich um Aktionen eines Benutzers, die eine optimistic oder detrimental Präferenz für einen bestimmten Artikel ausdrücken (z. B. das Anzeigen des Artikels on-line). Diese beiden Szenarien müssen häufig unterschiedlich behandelt werden.
Im Fall des MovieLens-Datensatzes haben wir Bewertungen, daher konzentrieren wir uns auf explizite Suggestions-Modelle. Zuerst müssen wir unsere Benutzer-Factor-Matrix erstellen. Wir können Benutzer-/Factor-IDs problemlos Benutzer-/Factor-Indizes zuordnen, indem wir den Offset „Python beginnt bei 0“ zwischen ihnen entfernen.
scores = np.zeros((n_users, n_items))
for row in df.itertuples():
scores(row(1)-1, row(2)-1) = row(3)
scores
array((( 5., 3., 4., ..., 0., 0., 0.),
( 4., 0., 0., ..., 0., 0., 0.),
( 0., 0., 0., ..., 0., 0., 0.),
...,
( 5., 0., 0., ..., 0., 0., 0.),
( 0., 0., 0., ..., 0., 0., 0.),
( 0., 5., 0., ..., 0., 0., 0.)))
sparsity = float(len(scores.nonzero()(0)))
sparsity /= (scores.form(0) * scores.form(1))
sparsity *= 100
print 'Sparsity: {:4.2f}%'.format(sparsity)
Sparsity: 6.30%
In diesem Datensatz hat jeder Benutzer mindestens 20 Filme bewertet, was zu einer angemessenen Spärlichkeit von 6,3 % führt. Das bedeutet, dass 6,3 % der Benutzerbewertung einen Wert haben. Beachten Sie, dass wir, obwohl wir fehlende Bewertungen als 0 eingetragen haben, nicht davon ausgehen sollten, dass diese Werte wirklich Null sind. Genauer gesagt handelt es sich lediglich um leere Einträge. Wir werden unsere Daten in Trainings- und Testsätze aufteilen, indem wir 10 Bewertungen professional Benutzer aus dem Trainingssatz entfernen und in den Testsatz einfügen.
def train_test_split(scores):
check = np.zeros(scores.form)
prepare = scores.copy()
for person in xrange(scores.form(0)):
test_ratings = np.random.alternative(scores(person, :).nonzero()(0),
measurement=10,
substitute=False)
prepare(person, test_ratings) = 0.
check(person, test_ratings) = scores(person, test_ratings)
# Take a look at and coaching are really disjoint
assert(np.all((prepare * check) == 0))
return prepare, check
prepare, check = train_test_split(scores)
Kollaboratives Filtern
Wir werden uns heute auf kollaborative Filtermodelle konzentrieren, die im Allgemeinen in zwei Klassen unterteilt werden können: benutzer- und artikelbasiertes kollaboratives Filtern. In beiden Szenarien wird eine Ähnlichkeitsmatrix erstellt. Beim benutzerbasierten kollaborativen Filtern besteht die Benutzerähnlichkeitsmatrix aus einer Distanzmetrik, die die Ähnlichkeit zwischen zwei beliebigen Benutzerpaaren misst. Ebenso misst die Artikelähnlichkeitsmatrix die Ähnlichkeit zwischen zwei beliebigen Artikelpaaren.
Eine gängige Distanzmetrik ist die Kosinusähnlichkeit. Die Metrik kann geometrisch betrachtet werden, wenn man die Zeile (Spalte) der Bewertungsmatrix eines bestimmten Benutzers (Components) als Vektor behandelt. Bei benutzerbasiertem kollaborativem Filtern wird die Ähnlichkeit zweier Benutzer als Kosinus des Winkels zwischen den Vektoren der beiden Benutzer gemessen. Für die Benutzer ${u}$ und ${u^{prime}}$ ist die Kosinusähnlichkeit
$$ sim(u, u^{prime}) = cos(theta{}) = frac{textbf{r}_{u} dot{} textbf{r}_{u^{prime}}}{| textbf{r}_{u} | | textbf{r}_{u^{prime}} |} = sum_{i} frac{r_{ui}r_{u^{prime}i}}{sqrt{sumlimits_{i} r_{ui}^2} sqrt{sumlimits_{i} r_{u^{prime}i}^2} } $$
Dies kann als For-Schleife mit Code geschrieben werden, aber der Python-Code wird ziemlich langsam ausgeführt. Stattdessen sollte man versuchen, jede Gleichung in Type von NumPy-Funktionen auszudrücken. Ich habe unten eine langsame und eine schnelle Model der Kosinus-Ähnlichkeitsfunktion eingefügt. Die langsame Funktion dauerte so lange, dass ich sie schließlich abgebrochen habe, weil ich des Wartens müde warfare. Die schnelle Funktion hingegen dauert etwa 200 ms.
Die Kosinusähnlichkeit liegt in unserem Fall zwischen 0 und 1 (da es keine negativen Bewertungen gibt). Beachten Sie, dass sie symmetrisch ist und Einsen entlang der Diagonale aufweist.
def slow_similarity(scores, form='person'):
if form == 'person':
axmax = 0
axmin = 1
elif form == 'merchandise':
axmax = 1
axmin = 0
sim = np.zeros((scores.form(axmax), scores.form(axmax)))
for u in xrange(scores.form(axmax)):
for uprime in xrange(scores.form(axmax)):
rui_sqrd = 0.
ruprimei_sqrd = 0.
for i in xrange(scores.form(axmin)):
sim(u, uprime) = scores(u, i) * scores(uprime, i)
rui_sqrd += scores(u, i) ** 2
ruprimei_sqrd += scores(uprime, i) ** 2
sim(u, uprime) /= rui_sqrd * ruprimei_sqrd
return sim
def fast_similarity(scores, form='person', epsilon=1e-9):
# epsilon -> small quantity for dealing with dived-by-zero errors
if form == 'person':
sim = scores.dot(scores.T) + epsilon
elif form == 'merchandise':
sim = scores.T.dot(scores) + epsilon
norms = np.array((np.sqrt(np.diagonal(sim))))
return (sim / norms / norms.T)
#%timeit slow_user_similarity(prepare)
%timeit fast_similarity(prepare, form='person')
1 loop, finest of three: 206 ms per loop
user_similarity = fast_similarity(prepare, form='person')
item_similarity = fast_similarity(prepare, form='merchandise')
print item_similarity(:4, :4)
(( 1. 0.4142469 0.33022352 0.44198521)
( 0.4142469 1. 0.26600176 0.48216178)
( 0.33022352 0.26600176 1. 0.3011288 )
( 0.44198521 0.48216178 0.3011288 1. ))
Mit unserer Ähnlichkeitsmatrix in der Hand können wir nun die Bewertungen vorhersagen, die nicht in den Daten enthalten waren. Mithilfe dieser Vorhersagen können wir sie dann mit den Testdaten vergleichen, um zu versuchen, die Qualität unseres Empfehlungsmodells zu validieren.
Beim benutzerbasierten kollaborativen Filtern sagen wir voraus, dass die Bewertung eines Benutzers $u$ für Factor $i$ durch die gewichtete Summe der Bewertungen aller anderen Benutzer für Factor $i$ gegeben ist, wobei die Gewichtung die Kosinus-Ähnlichkeit zwischen jedem Benutzer und dem Eingabebenutzer $u$ ist.
$$hat{r}_{ui} = sumlimits_{u^{prime}}sim(u, u^{prime}) r_{u^{prime}i}$$
Wir müssen auch nach der Anzahl der ${r_{u^{prime}i}}$-Bewertungen normalisieren:
$$hat{r}_{ui} = frac{sumlimits_{u^{prime}} sim(u, u^{prime}) r_{u^{prime}i}}{sumlimits_{u^{prime}}|sim(u, u^{prime})|}$$
Wie schon zuvor wird unsere Rechengeschwindigkeit erheblich davon profitieren, wenn wir NumPy-Funktionen gegenüber For-Schleifen bevorzugen. Bei unserer langsamen Funktion unten verlangsamt die Anwesenheit der For-Schleife den Algorithmus immer noch, obwohl ich NumPy-Methoden verwende.
def predict_slow_simple(scores, similarity, form='person'):
pred = np.zeros(scores.form)
if form == 'person':
for i in xrange(scores.form(0)):
for j in xrange(scores.form(1)):
pred(i, j) = similarity(i, :).dot(scores(:, j))
/np.sum(np.abs(similarity(i, :)))
return pred
elif form == 'merchandise':
for i in xrange(scores.form(0)):
for j in xrange(scores.form(1)):
pred(i, j) = similarity(j, :).dot(scores(i, :).T)
/np.sum(np.abs(similarity(j, :)))
return pred
def predict_fast_simple(scores, similarity, form='person'):
if form == 'person':
return similarity.dot(scores) / np.array((np.abs(similarity).sum(axis=1))).T
elif form == 'merchandise':
return scores.dot(similarity) / np.array((np.abs(similarity).sum(axis=1)))
%timeit predict_slow_simple(prepare, user_similarity, form='person')
1 loop, finest of three: 33.7 s per loop
%timeit predict_fast_simple(prepare, user_similarity, form='person')
1 loop, finest of three: 188 ms per loop
Wir verwenden die mittlere quadratische Fehlerfunktion von scikit-learn als Validierungsmetrik. Beim Vergleich von benutzer- und artikelbasiertem kollaborativem Filtern scheint es, als ob das benutzerbasierte kollaborative Filtern uns ein besseres Ergebnis liefert.
from sklearn.metrics import mean_squared_error
def get_mse(pred, precise):
# Ignore nonzero phrases.
pred = pred(precise.nonzero()).flatten()
precise = precise(precise.nonzero()).flatten()
return mean_squared_error(pred, precise)
item_prediction = predict_fast_simple(prepare, item_similarity, form='merchandise')
user_prediction = predict_fast_simple(prepare, user_similarity, form='person')
print 'Person-based CF MSE: ' + str(get_mse(user_prediction, check))
print 'Merchandise-based CF MSE: ' + str(get_mse(item_prediction, check))
Person-based CF MSE: 8.39140463389
Merchandise-based CF MSE: 11.5469590109
Kollaboratives Filtern der High-$ok$-Klasse
Wir können versuchen, unseren Vorhersage-MSE zu verbessern, indem wir nur die High-k-Benutzer berücksichtigen, die dem Eingabebenutzer am ähnlichsten sind (oder, analog, die High-k-Elemente). Das heißt, wenn wir die Summen über $u^{prime}$ berechnen
$$hat{r}_{ui} = frac{sumlimits_{u^{prime}} sim(u, u^{prime}) r_{u^{prime}i}}{sumlimits_{u^{prime}}|sim(u, u^{prime})|}$$
wir summieren nur über die obersten $ok$ Am ähnlichsten Benutzer. Unten wird eine langsame Implementierung dieses Algorithmus gezeigt. Obwohl ich sicher bin, dass es eine Möglichkeit gibt, die doppelten For-Schleifen durch Numpy-Sortierung loszuwerden, warfare ich beim Entschlüsseln der 2D-Argsort-Ausgabe ziemlich frustriert und habe mich einfach mit der langsamen Schleife zufrieden gegeben.
Wie unten gezeigt, halbiert sich unser Fehler durch die Anwendung dieser Methode tatsächlich!
def predict_topk(scores, similarity, form='person', ok=40):
pred = np.zeros(scores.form)
if form == 'person':
for i in xrange(scores.form(0)):
top_k_users = (np.argsort(similarity(:,i))(:-ok-1:-1))
for j in xrange(scores.form(1)):
pred(i, j) = similarity(i, :)(top_k_users).dot(scores(:, j)(top_k_users))
pred(i, j) /= np.sum(np.abs(similarity(i, :)(top_k_users)))
if form == 'merchandise':
for j in xrange(scores.form(1)):
top_k_items = (np.argsort(similarity(:,j))(:-ok-1:-1))
for i in xrange(scores.form(0)):
pred(i, j) = similarity(j, :)(top_k_items).dot(scores(i, :)(top_k_items).T)
pred(i, j) /= np.sum(np.abs(similarity(j, :)(top_k_items)))
return pred
pred = predict_topk(prepare, user_similarity, form='person', ok=40)
print 'High-k Person-based CF MSE: ' + str(get_mse(pred, check))
pred = predict_topk(prepare, item_similarity, form='merchandise', ok=40)
print 'High-k Merchandise-based CF MSE: ' + str(get_mse(pred, check))
High-k Person-based CF MSE: 6.47059807493
High-k Merchandise-based CF MSE: 7.75559095568
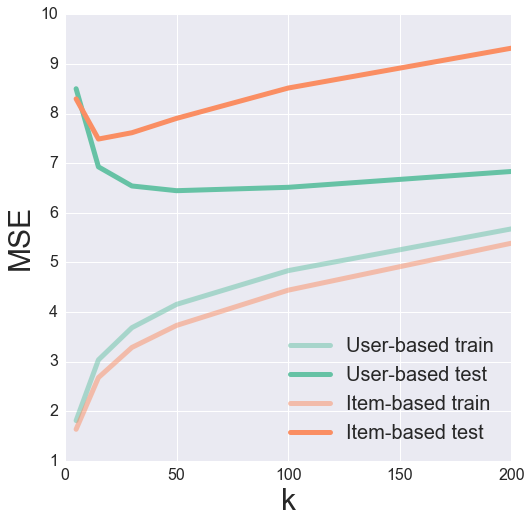
Wir können versuchen, den Parameter von $ok$ anzupassen, um den optimalen Wert zur Minimierung unseres Take a look at-MSE zu finden. Dabei hilft es oft, die Ergebnisse zu visualisieren, um ein Gefühl dafür zu bekommen, was vor sich geht.
k_array = (5, 15, 30, 50, 100, 200)
user_train_mse = ()
user_test_mse = ()
item_test_mse = ()
item_train_mse = ()
def get_mse(pred, precise):
pred = pred(precise.nonzero()).flatten()
precise = precise(precise.nonzero()).flatten()
return mean_squared_error(pred, precise)
for ok in k_array:
user_pred = predict_topk(prepare, user_similarity, form='person', ok=ok)
item_pred = predict_topk(prepare, item_similarity, form='merchandise', ok=ok)
user_train_mse += (get_mse(user_pred, prepare))
user_test_mse += (get_mse(user_pred, check))
item_train_mse += (get_mse(item_pred, prepare))
item_test_mse += (get_mse(item_pred, check))
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
pal = sns.color_palette("Set2", 2)
plt.determine(figsize=(8, 8))
plt.plot(k_array, user_train_mse, c=pal(0), label='Person-based prepare', alpha=0.5, linewidth=5)
plt.plot(k_array, user_test_mse, c=pal(0), label='Person-based check', linewidth=5)
plt.plot(k_array, item_train_mse, c=pal(1), label='Merchandise-based prepare', alpha=0.5, linewidth=5)
plt.plot(k_array, item_test_mse, c=pal(1), label='Merchandise-based check', linewidth=5)
plt.legend(loc='finest', fontsize=20)
plt.xticks(fontsize=16);
plt.yticks(fontsize=16);
plt.xlabel('ok', fontsize=30);
plt.ylabel('MSE', fontsize=30);
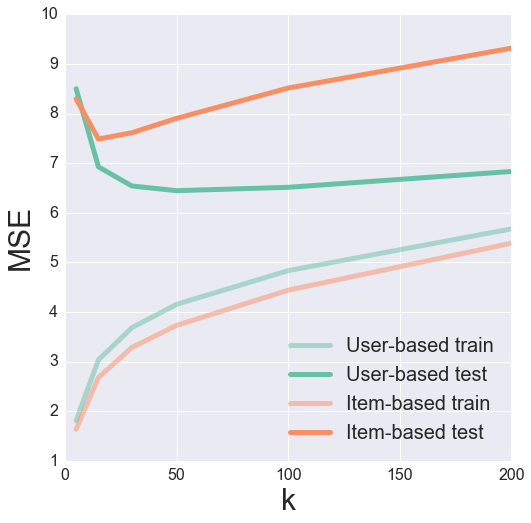
Es sieht aus wie ein ok von 50 bzw. 15 ergibt ein schönes Minimal des Testfehlers für benutzer- bzw. itembasiertes kollaboratives Filtern.
Bias-subtrahiertes kollaboratives Filtern
Für unsere letzte Methode zur Verbesserung der Empfehlungen werden wir versuchen, Verzerrungen zu beseitigen, die mit dem Benutzer des Artikels verbunden sind. Die Idee dabei ist, dass bestimmte Benutzer dazu neigen, allen Filmen immer hohe oder niedrige Bewertungen zu geben. Man könnte sich vorstellen, dass die relativer Unterschied in den Bewertungen dieser Benutzer ist wichtiger als die absolut Bewertungswerte.
Versuchen wir, die durchschnittliche Bewertung jedes Benutzers abzuziehen, wenn wir die Bewertungen ähnlicher Benutzer addieren, und diesen Durchschnitt am Ende wieder hinzuzufügen. Mathematisch sieht das so aus:
$$hat{r}_{ui} = bar{r_{u}} + frac{sumlimits_{u^{prime}} sim(u, u^{prime}) (r_{u^{prime}i} – bar{r_{u^{prime}}})}{sumlimits_{u^{prime}}|sim(u, u^{prime})|}$$
wobei $bar{r_{u}}$ die durchschnittliche Bewertung des Benutzers $u$ ist.
def predict_nobias(scores, similarity, form='person'):
if form == 'person':
user_bias = scores.imply(axis=1)
scores = (scores - user_bias(:, np.newaxis)).copy()
pred = similarity.dot(scores) / np.array((np.abs(similarity).sum(axis=1))).T
pred += user_bias(:, np.newaxis)
elif form == 'merchandise':
item_bias = scores.imply(axis=0)
scores = (scores - item_bias(np.newaxis, :)).copy()
pred = scores.dot(similarity) / np.array((np.abs(similarity).sum(axis=1)))
pred += item_bias(np.newaxis, :)
return pred
user_pred = predict_nobias(prepare, user_similarity, form='person')
print 'Bias-subtracted Person-based CF MSE: ' + str(get_mse(user_pred, check))
item_pred = predict_nobias(prepare, item_similarity, form='merchandise')
print 'Bias-subtracted Merchandise-based CF MSE: ' + str(get_mse(item_pred, check))
Bias-subtracted Person-based CF MSE: 8.67647634245
Bias-subtracted Merchandise-based CF MSE: 9.71148412222
Jetzt alle zusammen
Schließlich können wir versuchen, die beiden High-ok und die Bias-subtrahierten Algorithmen. Seltsamerweise scheint dies tatsächlich schlechter zu sein als die ursprünglichen High-ok Algorithmus. Das muss man sich mal vorstellen.
def predict_topk_nobias(scores, similarity, form='person', ok=40):
pred = np.zeros(scores.form)
if form == 'person':
user_bias = scores.imply(axis=1)
scores = (scores - user_bias(:, np.newaxis)).copy()
for i in xrange(scores.form(0)):
top_k_users = (np.argsort(similarity(:,i))(:-ok-1:-1))
for j in xrange(scores.form(1)):
pred(i, j) = similarity(i, :)(top_k_users).dot(scores(:, j)(top_k_users))
pred(i, j) /= np.sum(np.abs(similarity(i, :)(top_k_users)))
pred += user_bias(:, np.newaxis)
if form == 'merchandise':
item_bias = scores.imply(axis=0)
scores = (scores - item_bias(np.newaxis, :)).copy()
for j in xrange(scores.form(1)):
top_k_items = (np.argsort(similarity(:,j))(:-ok-1:-1))
for i in xrange(scores.form(0)):
pred(i, j) = similarity(j, :)(top_k_items).dot(scores(i, :)(top_k_items).T)
pred(i, j) /= np.sum(np.abs(similarity(j, :)(top_k_items)))
pred += item_bias(np.newaxis, :)
return pred
k_array = (5, 15, 30, 50, 100, 200)
user_train_mse = ()
user_test_mse = ()
item_test_mse = ()
item_train_mse = ()
for ok in k_array:
user_pred = predict_topk_nobias(prepare, user_similarity, form='person', ok=ok)
item_pred = predict_topk_nobias(prepare, item_similarity, form='merchandise', ok=ok)
user_train_mse += (get_mse(user_pred, prepare))
user_test_mse += (get_mse(user_pred, check))
item_train_mse += (get_mse(item_pred, prepare))
item_test_mse += (get_mse(item_pred, check))
pal = sns.color_palette("Set2", 2)
plt.determine(figsize=(8, 8))
plt.plot(k_array, user_train_mse, c=pal(0), label='Person-based prepare', alpha=0.5, linewidth=5)
plt.plot(k_array, user_test_mse, c=pal(0), label='Person-based check', linewidth=5)
plt.plot(k_array, item_train_mse, c=pal(1), label='Merchandise-based prepare', alpha=0.5, linewidth=5)
plt.plot(k_array, item_test_mse, c=pal(1), label='Merchandise-based check', linewidth=5)
plt.legend(loc='finest', fontsize=20)
plt.xticks(fontsize=16);
plt.yticks(fontsize=16);
plt.xlabel('ok', fontsize=30);
plt.ylabel('MSE', fontsize=30);
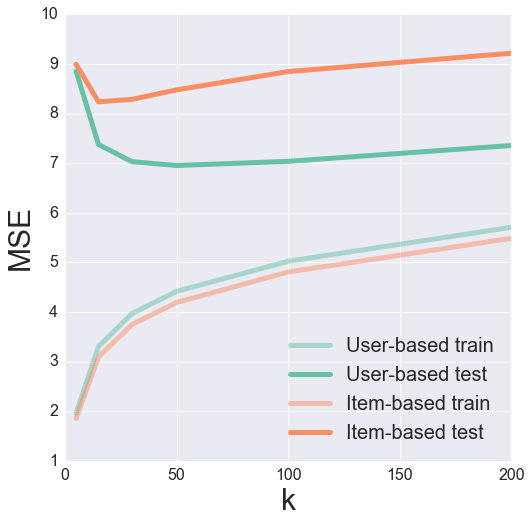
Validierung
Nachdem ich den grundlegenden Algorithmus für kollaboratives Filtern erläutert habe, habe ich gezeigt, wie wir unseren mittleren quadratischen Fehler mit zunehmender Modellkomplexität reduzieren können. Woher wissen wir jedoch wirklich, ob wir gute Empfehlungen abgeben? Eine Sache, die ich übersehen habe, warfare unsere Wahl der Ähnlichkeitsmetrik. Woher wissen wir, dass die Kosinus-Ähnlichkeit eine gute Metrik warfare? Da wir es mit einem Bereich zu tun haben, in dem viele von uns über Instinct verfügen (Filme), können wir uns unsere Elementähnlichkeitsmatrix ansehen und feststellen, ob ähnliche Elemente „Sinn ergeben“.
Und nur zum Spaß, lasst uns wirklich sehen bei den Artikeln. Der MovieLens-Datensatz enthält eine Datei mit Informationen zu jedem Movie. Es stellt sich heraus, dass es eine Web site namens themoviedb.org das eine kostenlose API hat. Wenn wir die IMDB-„Movie-ID“ für einen Movie haben, können wir diese API verwenden, um die Poster der Filme zurückzugeben. Wenn wir uns die Filmdatendatei unten ansehen, scheint es, dass wir zumindest die IMDB-URL für jeden Movie haben.
1|Toy Story (1995)|01-Jan-1995||http://us.imdb.com/M/title-exact?Toypercent20Storypercent20(1995)|0|0|0|1|1|1|0|0|0|0|0|0|0|0|0|0|0|0|0
2|GoldenEye (1995)|01-Jan-1995||http://us.imdb.com/M/title-exact?GoldenEyepercent20(1995)|0|1|1|0|0|0|0|0|0|0|0|0|0|0|0|0|1|0|0
3|4 Rooms (1995)|01-Jan-1995||http://us.imdb.com/M/title-exact?Fourpercent20Roomspercent20(1995)|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|1|0|0
4|Get Shorty (1995)|01-Jan-1995||http://us.imdb.com/M/title-exact?Getpercent20Shortypercent20(1995)|0|1|0|0|0|1|0|0|1|0|0|0|0|0|0|0|0|0|0
5|Copycat (1995)|01-Jan-1995||http://us.imdb.com/M/title-exact?Copycatpercent20(1995)|0|0|0|0|0|0|1|0|1|0|0|0|0|0|0|0|1|0|0
Wenn Sie einem der Hyperlinks in diesem Datensatz folgen, wird Ihre URL umgeleitet. Die resultierende URL enthält die IMDB-Movie-ID als letzte Info in der URL, beginnend mit „tt“. Die umgeleitete URL für Toy Story lautet beispielsweise http://www.imdb.com/title/tt0114709/und die IMDB-Movie-ID lautet tt0114709.
Mithilfe der Python-Anforderungsbibliothek können wir diese Movie-ID automatisch extrahieren. Das Toy Story-Beispiel wird unten angezeigt.
import requests
import json
response = requests.get('http://us.imdb.com/M/title-exact?Toypercent20Storypercent20(1995)')
print response.url.cut up('/')(-2)
tt0114709
Ich habe einen kostenlosen API-Schlüssel von themoviedb.org angefordert. Der Schlüssel ist für die Abfrage der API erforderlich. Ich habe ihn unten weggelassen, additionally seien Sie sich bewusst, dass Sie Ihren eigenen Schlüssel benötigen, wenn Sie dies reproduzieren möchten. Wir können nach Filmplakaten anhand der Movie-ID suchen und dann Hyperlinks zu den Bilddateien abrufen. Die Hyperlinks sind relative Pfade, daher benötigen wir die base_url-Abfrage oben in der nächsten Zelle, um den vollständigen Pfad zu erhalten. Außerdem funktionieren einige der Hyperlinks nicht, daher können wir stattdessen nach dem Movie anhand des Titels suchen und das erste Ergebnis abrufen.
# Get base url filepath construction. w185 corresponds to measurement of film poster.
headers = {'Settle for': 'software/json'}
payload = {'api_key': 'INSERT API KEY HERE'}
response = requests.get("http://api.themoviedb.org/3/configuration", params=payload, headers=headers)
response = json.masses(response.textual content)
base_url = response('photos')('base_url') + 'w185'
def get_poster(imdb_url, base_url):
# Get IMDB film ID
response = requests.get(imdb_url)
movie_id = response.url.cut up('/')(-2)
# Question themoviedb.org API for film poster path.
movie_url = 'http://api.themoviedb.org/3/film/{:}/photos'.format(movie_id)
headers = {'Settle for': 'software/json'}
payload = {'api_key': 'INSERT API KEY HERE'}
response = requests.get(movie_url, params=payload, headers=headers)
attempt:
file_path = json.masses(response.textual content)('posters')(0)('file_path')
besides:
# IMDB film ID is typically no good. Must get right one.
movie_title = imdb_url.cut up('?')(-1).cut up('(')(0)
payload('question') = movie_title
response = requests.get('http://api.themoviedb.org/3/search/film', params=payload, headers=headers)
movie_id = json.masses(response.textual content)('outcomes')(0)('id')
payload.pop('question', None)
movie_url = 'http://api.themoviedb.org/3/film/{:}/photos'.format(movie_id)
response = requests.get(movie_url, params=payload, headers=headers)
file_path = json.masses(response.textual content)('posters')(0)('file_path')
return base_url + file_path
from IPython.show import Picture
from IPython.show import show
toy_story = 'http://us.imdb.com/M/title-exact?Toypercent20Storypercent20(1995)'
Picture(url=get_poster(toy_story, base_url))

Tada! Jetzt haben wir eine Pipeline, die uns direkt von der IMDB-URL in der Datendatei zur Anzeige des Filmplakats führt. Mit dieser Maschinerie in der Hand wollen wir unsere Filmähnlichkeitsmatrix untersuchen.
Wir können ein Wörterbuch erstellen, um die Filmindizes aus unserer Ähnlichkeitsmatrix den URLs der Filme zuzuordnen. Wir erstellen auch eine Hilfsfunktion, um die High-ok ähnlichste Filme bei einem bestimmten Eingabefilm. Mit dieser Funktion ist der erste zurückgegebene Movie der Eingabefilm (weil er natürlich sich selbst am ähnlichsten ist).
# Load in film knowledge
idx_to_movie = {}
with open('u.merchandise', 'r') as f:
for line in f.readlines():
data = line.cut up('|')
idx_to_movie(int(data(0))-1) = data(4)
def top_k_movies(similarity, mapper, movie_idx, ok=6):
return (mapper(x) for x in np.argsort(similarity(movie_idx,:))(:-ok-1:-1))
idx = 0 # Toy Story
films = top_k_movies(item_similarity, idx_to_movie, idx)
posters = tuple(Picture(url=get_poster(film, base_url)) for film in films)
Hmmm, diese Empfehlungen scheinen nicht so intestine zu sein! Schauen wir uns noch ein paar an.
Wie Sie sehen, haben wir vielleicht von Anfang an keine so gute Ähnlichkeitsmatrix verwendet. Einige dieser Empfehlungen sind ziemlich schlecht – Star Wars ist der Movie, der Toy Story am ähnlichsten ist? Kein anderer James-Bond-Movie in den High 5 der Filme, die GoldenEye am ähnlichsten sind?
Ein mögliches Drawback ist, dass sehr beliebte Filme wie Star Wars bevorzugt werden. Wir können diese Verzerrung teilweise beseitigen, indem wir eine andere Ähnlichkeitsmetrik berücksichtigen – die Pearson-Korrelation. Ich verwende einfach die integrierte Scikit-Study-Funktion, um dies zu berechnen.
from sklearn.metrics import pairwise_distances
# Convert from distance to similarity
item_correlation = 1 - pairwise_distances(prepare.T, metric='correlation')
item_correlation(np.isnan(item_correlation)) = 0.
Schauen wir uns diese Filme noch einmal an.
Obwohl sich die Reihenfolge etwas geändert hat, haben wir im Großen und Ganzen dieselben Filme zurückgegeben. Jetzt können Sie sehen, warum Empfehlungssysteme so ein kniffliges Unterfangen sind! Nächstes Mal werden wir fortgeschrittenere Modelle untersuchen und sehen, wie sie sich auf die Empfehlungen auswirken.
Um zum ursprünglichen IPython-Pocket book zu gelangen, das zum Generieren dieses Beitrags verwendet wurde, klicken Sie auf Hier