Dieser Beitrag stammt von Bob
Ich habe in letzter Zeit über die Bewertung nachgedacht, weil ich mit Kollegen daran gearbeitet habe neu Samplerwas bedeutet, zu bewerten, wie intestine sie funktionieren (mehr dazu bald). Dies wiederum bedeutet, Zieldichten zu finden, auf denen sie bewertet werden können.
Ein kombinatorischer multimodaler Testfall
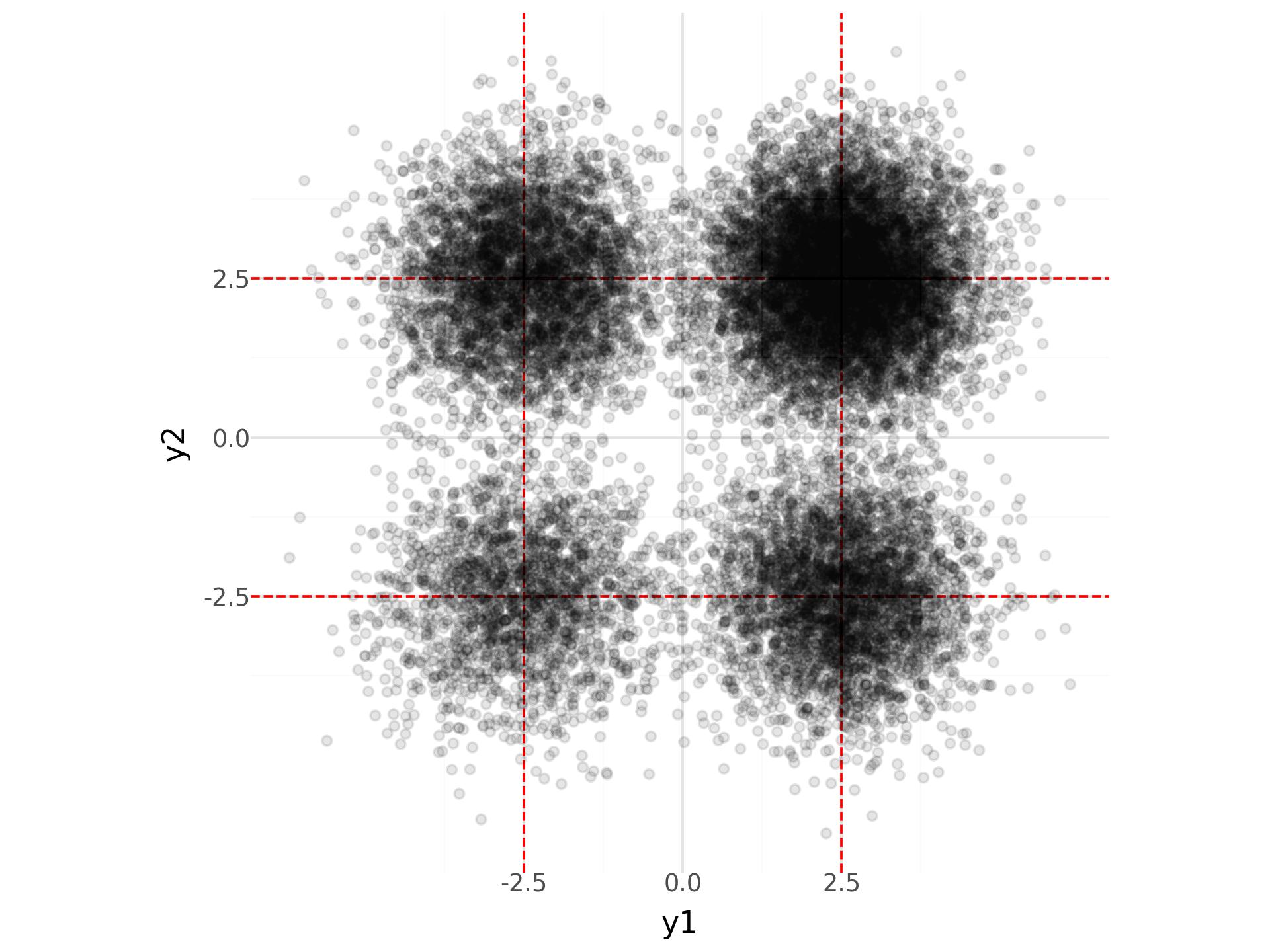
Ich wollte etwas klar multimodal und daher nicht konkav log. Ich erinnere mich, dass jemandes Papier (Hilfe beim Zitat?) Eine Mischung aus vier zweidimensionalen isotropen Normalen verwendet hat, die genug getrennt sind, um den Übergang möglich zu machen, aber immer noch ein bisschen schwierig. Nicht um das Spiel zu verschenken, aber hier ist eine hintere Handlung einer Probe, die aus Stan gezogen wurde – das Ungleichgewicht in Komponentengewichten ist beabsichtigt, wie ich unten beschreiben werde.

Ich arbeite immer noch daran posteriordb mit der Stan Gang (siehe die Autoren des verknüpften Papiers) und Inferenz -Fitnessstudio mit Reuben Cohn-Gordon (Ein weiterer Linguist, der von Coaching und Programmiersprache Geek zu MCMC gewandt hat) und dachte, es wäre schön, etwas allgemeineres als nur das 2D -Beispiel zu haben. Additionally habe ich mein Notizbuch herausgeholt und die Verallgemeinerung auf D-Abmessungen festgestellt, die 2^D-Mischkomponenten umfasst, die regular sind, wobei die Einheit-Kovarianz an den Punkten in {-r, r}^d liegt.
p(y | r) = SUM_{mu in {-r, r}^D} 1/2^D regular(y | mu, I).
Ich habe dann verallgemeinert, damit die Wahrscheinlichkeit festgelegt wird, dass y (d)> 0 p in (0, 1) eine ungleichmäßige Mischung erhalten kann. Dies führt aufgrund der Ungleichmäßigkeit zu einer etwas komplexeren Dichte.
p(y | r) = SUM_{mu in {-r, r}^D} binomial(sum(mu == r) | D, p) * regular(y | mu, I).
Codierung in Stan mit Fortsetzung des Passing-Stils
Wie codieren wir das in Stan? Offensichtlich muss es rekursiv oder zumindest iterativ sein, damit das D zur Zusammenstellung unbekannt ist. Wann immer ich eine Rekursion sehe, denke ich sofort daran Fortsetzung des Passstils (CPS). Additionally habe ich dieses STAN -Programm entwickelt, um eine Verallgemeinerung in D -Dimensionen zu codieren.
features {
actual mm(vector y, actual r, actual p, int d, actual lp) {
if (d == 0) {
return lp;
}
actual lp1 = mm(y, r, p, d - 1, lp + normal_lpdf(y(d) | r, 1));
actual lp2 = mm(y, r, p, d - 1, lp + normal_lpdf(y(d) | -r, 1));
return log_mix(p, lp1, lp2);
}
actual mm_lpdf(vector y, actual r, actual p, int D) {
return mm(y, r, p, D, 0);
}
}
information {
int D; // variety of dimensions
actual r; // modes in {-r, r}^D
actual p; // p = Pr(Y(d) > 0)
}
parameters {
vector(D) y;
}
mannequin {
y ~ mm(r, p, D);
}
Die Funktion log_mix ist wie folgt definiert, aber stabiler implementiert.
log_mix(p, lp1, lp2)
= log_sum_exp(log(p) + lp1, log(1 - p) + lp2)
= log(exp(log(p) + lp1) + exp(log(1 - p) + lp2))
= log(p * exp(lp1) + (1 - p) * exp(lp2)).
Wenn Sie die Rekursion manuell entfalten, sind die Blätter die Holzdichten und die Gewichte landen wie in der Definition beschrieben. Wenn Sie Schwierigkeiten haben, dies zu sehen, hilft die manuelle Erweiterung der d = 1 und dann d = 2. Es ist kompakt, aber es ist immer noch exponentiell, eine Protokolldichte und einen Gradienten zu bewerten (dh O (2^d)). Obwohl es in höheren Dimensionen langsam ist, funktioniert es.
Python -Skripte
Das obige Diagramm stammt aus dem folgenden Python -Code, der festgelegt wird
D = 2, r = 2,5 und p = 2,0/3,0.
Für diejenigen unter Ihnen, die einen Umzug nach Python in Betracht ziehen, ist es ein Glücksfall, einen Klon von Datenrahmen (Pandas) und GGPlot2 (Plotnine) zu haben. Und ja, natürlich wissen die LLMs, wie man Pandas und Plotnine codiert.
import cmdstanpy as csp
import pandas as pd
import plotnine as pn
mannequin = csp.CmdStanModel(stan_file="mm.stan")
D = 2
r = 2.5
p = 2.0 / 3.0
information = {'D': D, 'r': r, 'p': p}
match = mannequin.pattern(information = information, iter_sampling=5_000)
print(match.abstract(sig_figs=2))
y = match.stan_variable('y')
df = pd.DataFrame({'y1': y(:, 0), 'y2': y(:, 1)})
plot = (
pn.ggplot(df, pn.aes(x='y1', y='y2'))
+ pn.geom_vline(xintercept=(-r, r), coloration="purple", linetype="dashed")
+ pn.geom_hline(yintercept=(-r, r), coloration="purple", linetype="dashed")
+ pn.geom_point(alpha=0.1)
+ pn.scale_x_continuous(breaks=(-r, 0, r))
+ pn.scale_y_continuous(breaks=(-r, 0, r))
+ pn.coord_fixed()
+ pn.theme_minimal()
)
plot.save('mm.jpg', dpi=300)
Der Abschlag von Datenrahmen in Pandas und GGPLOT2 in Plotnine ist ein Glücksfall, wenn Sie von R nach Python wechseln (was ich sehr empfehlen würde).
Dynamische Programmierung zur Rettung
Weil es CPS beteiligte, habe ich es verschickt Brian Ward Gegen Mitternacht letzte Nacht. Ich bin ein anständiger Programmierer, aber Brians nächstes Degree. Als ich heute um 10 Uhr ankam, hatte er die Zieldichte wie folgt neu geschrieben.
actual mm_lpdf(vector y, actual r, actual p, int d) {
if (d == 0) {
return 0;
}
actual lower_mixture = mm_lpdf(y | r, p, d - 1);
actual lp1 = lower_mixture + normal_lpdf(y(d) | r, 1);
actual lp2 = lower_mixture + normal_lpdf(y(d) | -r, 1);
return log_mix(p, lp1, lp2);
}
(Bearbeiten: Durch eine Mischung aus LPDF und LUPDF.
Er sah, dass die Rekursionen in jedem Zweig dasselbe machten und geteilt werden konnten. Da es nur einen rekursiven Anruf gibt, ist Brians Code linear (dh O (d)). Es erreicht diese Beschleunigung mithilfe der dynamischen Programmierung (DP). DP berechnet Teillösungen, die zu größeren Lösungen kombiniert werden können, anstatt sie neu zu berechnen. DP ist die Technik, die Sie benötigen, um die härteren L33T-Code-Checks zu lösen, die Sie heutzutage während technischer Interviews erhalten. Weitere Beispiele, bei denen DP für statistische Modelle hilfreich sein kann, umfassen die Quick Fourier-Transformation (FFT), den Vorwärtsalgorithmus für versteckte Markov-Modelle (HMMs) und die Poisson-Binomial-Verteilung. Die ersten beiden werden in Stan und letzterem effizient codiert, wie ich in a codieren kann Stan Discussion board Submit auf Poisson-Binomial.
Probieren Sie es selbst auf dem Stan -Spielplatz aus
Wenn Sie selbst damit spielen möchten, baute Brian eine Model mit dem Stan -Spielplatz, auf dem Sie im Browser laufen können.
- Stan -Spielplatz: Kombinatorische normale Gemische
So sieht es nach dem Einstellen von D = 3 aus, ausführte Stichproben und dann ein Histogramm mit allen drei ausgewählten Dimensionen anzusehen.

Es ist eine Stay -Demo, sodass Sie die Daten auf R, D und p bearbeiten können. Und es ist sehr schnell aufgrund des DP. Genau wie in Shinystan und vor allem seine generische Model im Browser McMcMonitor (Von vielen der gleichen Entwickler wie Stan-Spielplatz) können Sie 3D-Projektionen der höherdimensionalen Zeichnen anzeigen und sie drehen, um zu sehen, dass 8 Bälle in 3D hergestellt werden, von denen 7 im Bildschirmgreifer sichtbar sind. Oder Sie können zu höheren Dimensionen gehen und Projektionen auf zwei oder drei Dimensionen anzeigen. Möglicherweise möchten Sie die Anzahl der Ziehungen professional Kette erhöhen, um die posterioren Dichten in den Visualisierungen sauberer abzugrenzen.