Viel wird in diesem Weblog über „Publish -Stratifikation“ geschrieben. Andrew spricht es formell mit einem an “Herr„. Aber als ich es gelernt habe Alan Zaslavskys Kurs Es struggle beiläufig nur „nach Stratifizierung“. Zu der Zeit klang es für mich wie Schadenskontrolle, nachdem wir vergessen hatten, zu schichten.

- “Schichtung”= Teilen Sie die Inhabitants in Schichten (dh Gruppen) anhand einiger Variablen X auf. Soziale Hierarchienaber um Repräsentativität zu zielen. Wenn wir schichten vor Wenn wir das Beispiel auswählen, können wir eine Probe in jeder Schicht zur Repräsentativität nehmen.
- “Publish”= Teilen Sie die Bevölkerung nur in Schichten auf nach Die Probe ist bereits ausgewählt.
Ausgefallene Grafiken von a DOL Video Ich habe daran gearbeitet:

Wie kann die Publish -Stratifizierung helfen?
Angenommen, wir wollen E (y), die Bevölkerung, schätzen. Aber wir haben nur Y in der Umfrage -Stichprobe. Nehmen wir zum Beispiel an, Y stimmt republikanisch ab. Wir können den Probenmittelwert verwenden, Ybar = Ehat (y | pattern) (Ich weiß nicht, wie man in diesem Weblog Latexpause latert).
Aber unser Stichprobenmittelwert ist bedingt beim Abtasten. Und was ist, wenn Umfrageteilnehmer mehr oder weniger republikanisch als die Bevölkerung sind? Wie Joe Blitzstein uns lehrt: „Konditionierung ist die Seele der Statistiken.“ Die Konditionierung des Probens kann unsere Schätzung beeinflussen. Aber vielleicht kann uns auch mehr Konditionierung helfen?! Joe lehrte mich, die Konditionierung zu versuchen, wenn ich stecken bleibe.

Wenn wir Bevölkerungsdaten zu X, z. B. Rassengruppe Das Gesetz der Gesamterwartung (Joes Favorit): E (y) = e (e (y | x)). Wenn unsere Stichprobe additionally die falsche Verteilung von Rassengruppen aufweist, beheben wir das zumindest mit einer gewissen Kalibrierung. Ersetzen von „E“ durch Schätzungen „Ehat“, poststratifizierende Schätzungen E (y) durch E (Ehat (y | x, Probe)).
Wenn unsere Schätzung von E (y | x) der Stichprobenmittelwert von y für Leute mit diesem x ist, ist die aggregierte Schätzung die klassische Nachstratifizierung, yhat_ps. Wenn unsere Schätzung von E (y | x) auf einem Modell basiert, das über x reguliert wird, ist die Aggregatschätzung eine Mehrebenenregression (“Herr“) Und Poststratifikation, yhat_mrp. Gelman 2007 zeigt, wie yhat_mrp eine Schrumpfung von yhat_ps in Richtung Ybar ist.
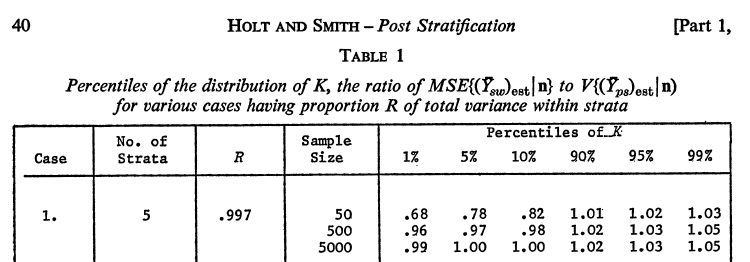
Welche Schätzung eignet sich am besten zur Schätzung von E (Y)? ybar, yhat_ps oder yhat_mrp?
Als Kuh et al. 2023 schreiben:
Es sind keine individuellen Vorhersagen, die intestine sein müssen, sondern die Aggregationen dieser individuellen Schätzungen.
Ein paralleler Ansatz erfolgt durch Simulationsstudien – für einen größeren Realismus, diese können häufig unter Verwendung von Teilproben tatsächlicher Umfragen konstruiert werden – sowie theoretische Untersuchungen der Verzerrung und Varianz poststratifizierter Schätzungen mit moderaten Stichprobengrößen.