Kurz zusammengefasst: Wir schlagen vor, asymmetrische zertifizierte Robustheit Drawback, das zertifizierte Robustheit für nur eine Klasse erfordert und reale gegnerische Szenarien widerspiegelt. Diese fokussierte Einstellung ermöglicht es uns, merkmalskonvexe Klassifikatoren einzuführen, die geschlossene und deterministische zertifizierte Radien in der Größenordnung von Millisekunden erzeugen.

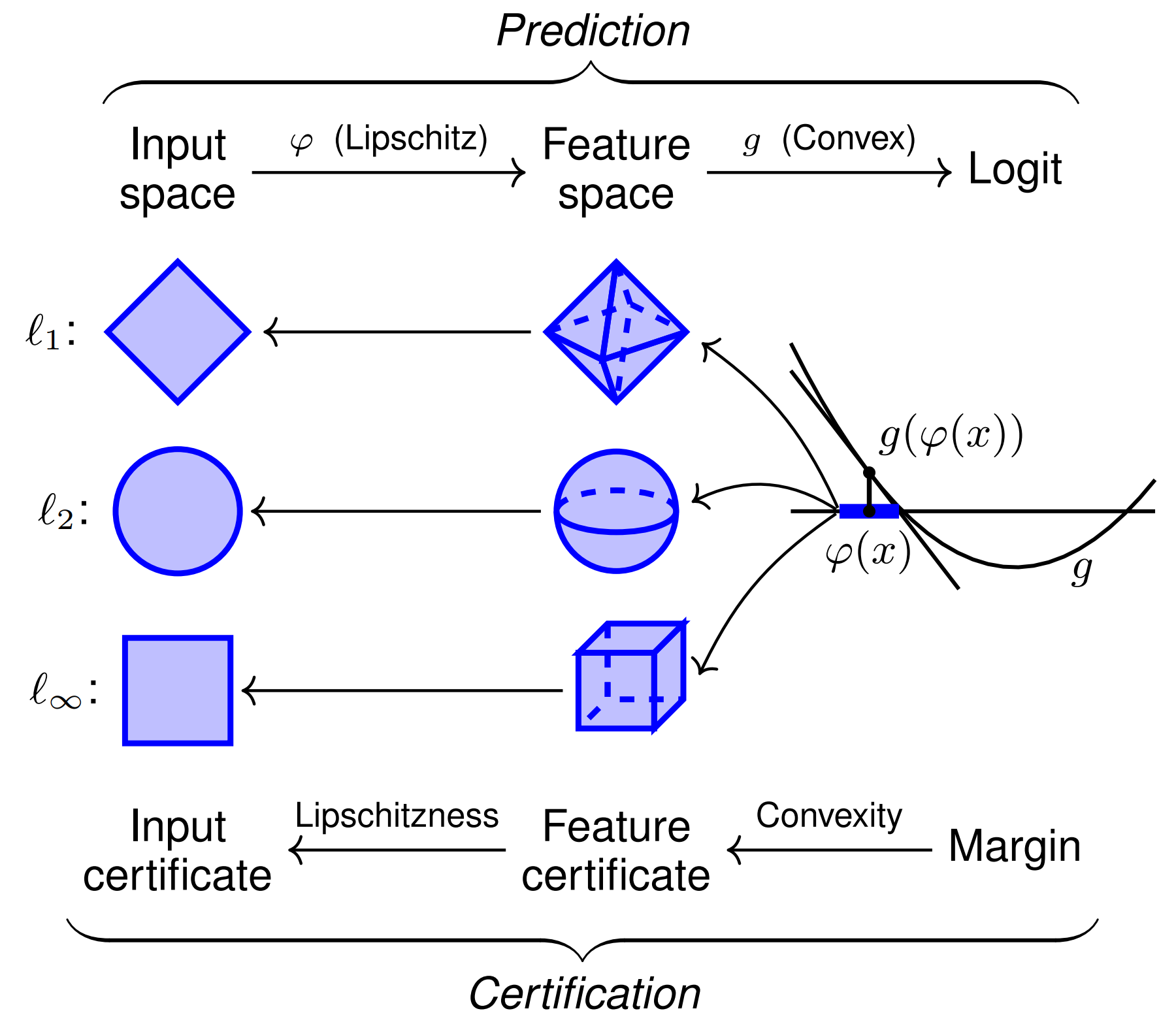
Abbildung 1. Darstellung von merkmalskonvexen Klassifikatoren und ihrer Zertifizierung für Eingaben sensibler Klassen. Diese Architektur erstellt eine Lipschitz-kontinuierliche Merkmalskarte $varphi$ mit einer gelernten konvexen Funktion $g$. Da $g$ konvex ist, wird es international durch seine Tangentialebene bei $varphi(x)$ unterapproximiert, was zertifizierte Normbälle im Merkmalsraum ergibt. Die Lipschitzheit von $varphi$ ergibt dann entsprechend skalierte Zertifikate im ursprünglichen Eingaberaum.
Trotz ihrer weiten Verbreitung sind Deep Studying-Klassifikatoren äußerst anfällig für kontroverse Beispiele: kleine, für den Menschen nicht wahrnehmbare Bildstörungen, die maschinelle Lernmodelle dazu verleiten, die modifizierte Eingabe falsch zu klassifizieren. Diese Schwäche untergräbt die Zuverlässigkeit sicherheitskritischer Prozesse, die maschinelles Lernen beinhalten, erheblich. Es wurden viele empirische Abwehrmaßnahmen gegen feindliche Störungen vorgeschlagen – oft nur, um später durch stärkere Angriffsstrategien besiegt zu werden. Wir konzentrieren uns daher auf Zertifizierbar robuste Klassifikatorendie eine mathematische Garantie dafür bieten, dass ihre Vorhersage für eine $ell_p$-Normkugel um eine Eingabe konstant bleibt.
Herkömmliche Methoden zur zertifizierten Robustheit haben eine Reihe von Nachteilen, darunter Nichtdeterminismus, langsame Ausführung, schlechte Skalierung und Zertifizierung nur für eine Angriffsnorm. Wir argumentieren, dass diese Probleme angegangen werden können, indem das Drawback der zertifizierten Robustheit verfeinert wird, um es besser an praktische gegnerische Situationen anzupassen.
Das Drawback der asymmetrischen zertifizierten Robustheit
Aktuelle nachweislich robuste Klassifizierer erstellen Zertifikate für Eingaben, die zu einer beliebigen Klasse gehören. Für viele reale gegnerische Anwendungen ist dies unnötig weit gefasst. Betrachten Sie den anschaulichen Fall eines Menschen, der eine Phishing-E-Mail verfasst und gleichzeitig versucht, Spamfilter zu umgehen. Dieser Angreifer wird immer versuchen, den Spamfilter zu täuschen, indem er ihn glauben lässt, dass seine Spam-E-Mail harmlos ist – niemals umgekehrt. Mit anderen Worten: Der Angreifer versucht lediglich, falsche Negativergebnisse vom Klassifikator zu erhalten. Ähnliche Einstellungen umfassen die Erkennung von Malware, die Kennzeichnung von Pretend Information, die Erkennung von Social-Media-Bots, das Filtern von Krankenversicherungsansprüchen, die Erkennung von Finanzbetrug, die Erkennung von Phishing-Web sites und vieles mehr.
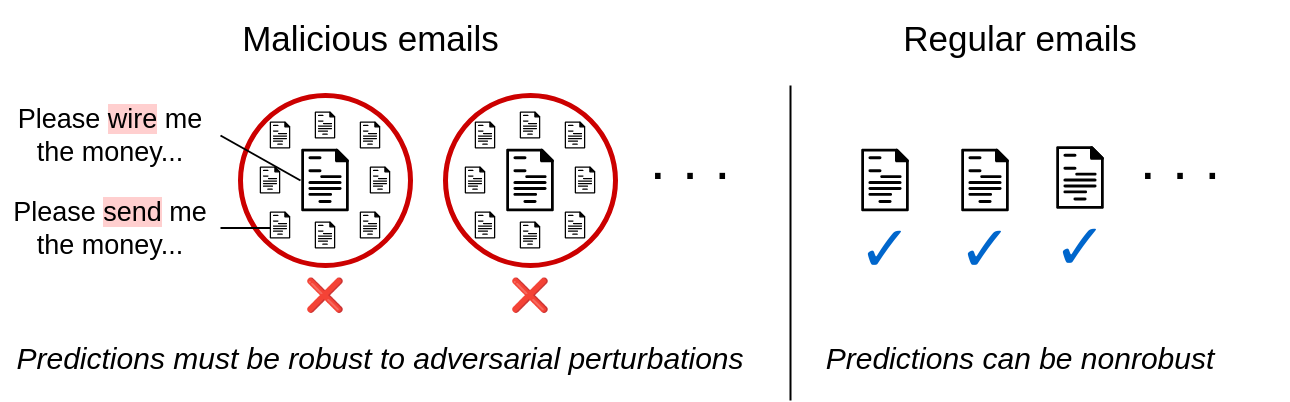
Abbildung 2. Asymmetrische Robustheit bei der E-Mail-Filterung. In der Praxis ist in gegnerischen Umgebungen oft zertifizierte Robustheit nur für eine Klasse erforderlich.
Bei allen diesen Anwendungen handelt es sich um eine binäre Klassifizierungseinstellung mit einer smart Klasse die ein Angreifer zu vermeiden versucht (z. B. die Klasse „Spam-E-Mail“). Dies motiviert das Drawback der asymmetrische zertifizierte Robustheitdessen Ziel darin besteht, nachweislich robuste Vorhersagen für Eingaben in der sensiblen Klasse zu liefern und gleichzeitig eine hohe Genauigkeit für alle anderen Eingaben beizubehalten. Wir liefern im Haupttext eine formellere Problemstellung.
Merkmalskonvexe Klassifikatoren
Wir schlagen vor Merkmalskonvexe neuronale Netze um das Drawback der asymmetrischen Robustheit zu lösen. Diese Architektur komponiert eine einfache Lipschitz-kontinuierliche Function-Map ${varphi: mathbb{R}^d to mathbb{R}^q}$ mit einem gelernten Enter-Convex Neural Community (ICNN) ${g: mathbb{R}^q to mathbb{R}}$ (Abbildung 1). ICNNs erzwingen Konvexität vom Enter- zum Output-Logit, indem sie ReLU-Nichtlinearitäten mit nichtnegativen Gewichtsmatrizen komponieren. Da ein binärer ICNN-Entscheidungsbereich aus einem konvexen Set und seinem Komplement besteht, fügen wir die vorkomponierte Function-Map $varphi$ hinzu, um nichtkonvexe Entscheidungsbereiche zu ermöglichen.
Merkmalskonvexe Klassifikatoren ermöglichen die schnelle Berechnung von zertifizierten Radien empfindlicher Klassen für alle $ell_p$-Normen. Unter Ausnutzung der Tatsache, dass konvexe Funktionen international von jeder Tangentialebene unterapproximiert werden, können wir einen zertifizierten Radius im Zwischenmerkmalsraum erhalten. Dieser Radius wird dann durch Lipschitzness in den Eingaberaum übertragen. Die asymmetrische Einstellung ist hier kritisch, da diese Architektur nur Zertifikate für die constructive Logit-Klasse $g(varphi(x)) > 0$ erzeugt.
Die resultierende, nach der $ell_p$-Norm zertifizierte Radiusformel ist besonders elegant:
(r_p(x) = frac{ shade{blue}{g(varphi(x))} } { mathrm{Lip}_p(varphi) shade{purple}{| nabla g(varphi(x)) | _{p,*}}}.)
Die nicht-konstanten Terme sind leicht zu interpretieren: Der Radius skaliert proportional zur Klassifikatorvertrauen und umgekehrt zum Klassifikatorempfindlichkeit. Wir bewerten diese Zertifikate anhand einer Reihe von Datensätzen und erzielen wettbewerbsfähige $ell_1$-Zertifikate und vergleichbare $ell_2$- und $ell_{infty}$-Zertifikate – obwohl andere Methoden im Allgemeinen auf eine bestimmte Norm zugeschnitten sind und um Größenordnungen mehr Laufzeit erfordern.
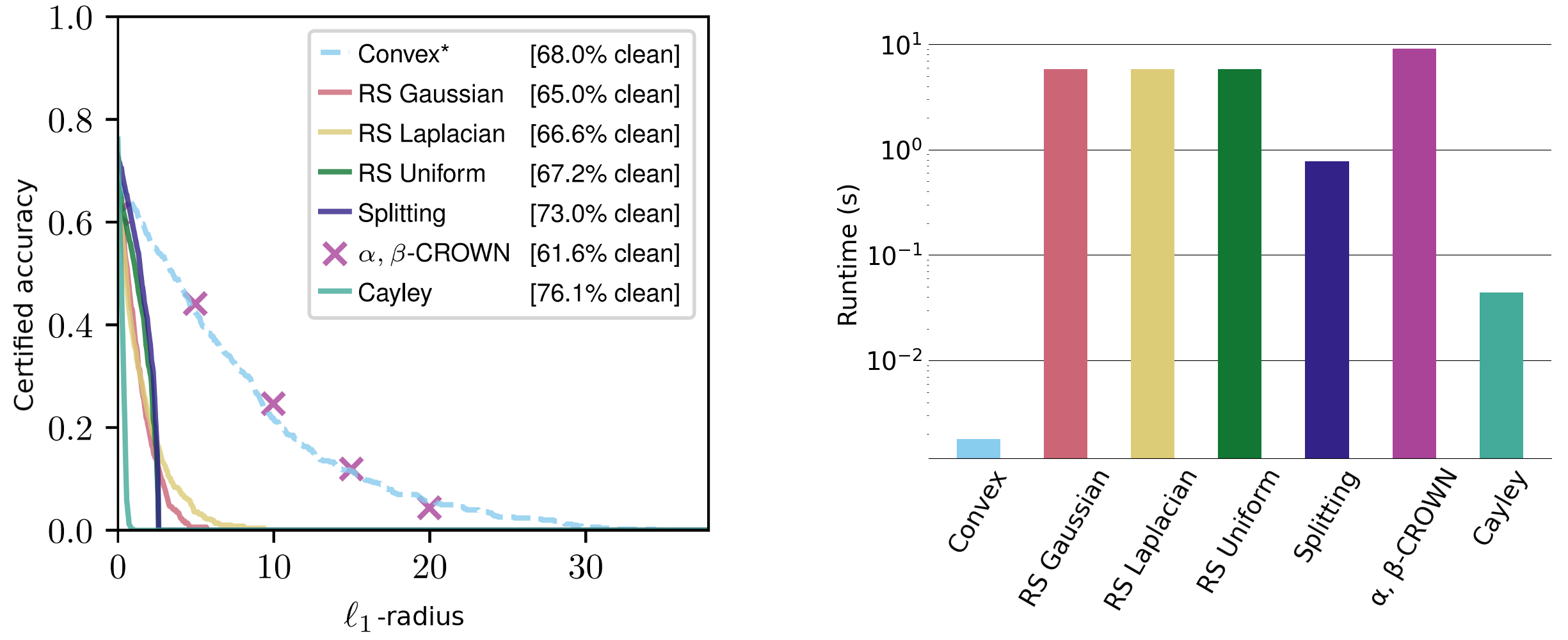
Abbildung 3. Zertifizierte Radien der empfindlichen Klasse im CIFAR-10-Datensatz „Katzen vs. Hunde“ für die $ell_1$-Norm. Die Laufzeiten auf der rechten Seite sind über die $ell_1$-, $ell_2$- und $ell_{infty}$-Radien gemittelt (beachten Sie die logarithmische Skalierung).
Unsere Zertifikate gelten für jede $ell_p$-Norm und sind geschlossen und deterministisch, sodass professional Eingabe nur ein Vorwärts- und Rückwärtsdurchlauf erforderlich ist. Diese sind in der Größenordnung von Millisekunden berechenbar und lassen sich intestine mit der Netzwerkgröße skalieren. Zum Vergleich: Aktuelle hochmoderne Methoden wie randomisierte Glättung und Intervall-Grenzausbreitung benötigen in der Regel mehrere Sekunden, um selbst kleine Netzwerke zu zertifizieren. Randomisierte Glättungsmethoden sind außerdem von Natur aus nichtdeterministisch, mit Zertifikaten, die mit hoher Wahrscheinlichkeit einfach gelten.
Theoretisches Versprechen
Während die ersten Ergebnisse vielversprechend sind, deutet unsere theoretische Arbeit darauf hin, dass ICNNs auch ohne Function-Map noch erhebliches ungenutztes Potenzial haben. Obwohl binäre ICNNs auf das Lernen konvexer Entscheidungsbereiche beschränkt sind, beweisen wir, dass es ein ICNN gibt, das im CIFAR-10-Katzen-gegen-Hunde-Datensatz eine perfekte Trainingsgenauigkeit erreicht.
Tatsache. Es gibt einen Enter-konvexen Klassifikator, der eine perfekte Trainingsgenauigkeit für den CIFAR-10-Katzen-gegen-Hunde-Datensatz erreicht.
Unsere Architektur erreicht jedoch ohne eine Function-Map nur eine Trainingsgenauigkeit von 73,4 %. Obwohl die Trainingsleistung keine Generalisierung des Testsatzes impliziert, deutet dieses Ergebnis darauf hin, dass ICNNs zumindest theoretisch in der Lage sind, das moderne Paradigma des maschinellen Lernens der Überanpassung an den Trainingsdatensatz zu erreichen. Wir stellen daher das folgende offene Drawback für das Feld dar.
Offenes Drawback. Lernen Sie einen inputkonvexen Klassifikator kennen, der eine perfekte Trainingsgenauigkeit für den CIFAR-10-Katzen-gegen-Hunde-Datensatz erreicht.
Abschluss
Wir hoffen, dass das asymmetrische Robustheits-Framework zu neuen Architekturen inspiriert, die in diesem fokussierteren Umfeld zertifizierbar sind. Unser Function-konvexer Klassifikator ist eine solche Architektur und bietet schnelle, deterministische zertifizierte Radien für jede $ell_p$-Norm. Wir stellen auch das offene Drawback der Überanpassung des CIFAR-10-Trainingsdatensatzes „Katzen vs. Hunde“ mit einem ICNN, was, wie wir zeigen, theoretisch möglich ist.
Dieser Beitrag basiert auf dem folgenden Dokument:
Asymmetrische zertifizierte Robustheit durch Function-Convex Neural Networks
Samuel Pfrommer,
Brendon G. Anderson,
Julien Piet,
Somayeh Sojoudi,
37. Konferenz zu neuronalen Informationsverarbeitungssystemen (NeurIPS 2023).
Weitere Einzelheiten finden Sie auf arXiv Und GitHub. Wenn unser Papier Ihre Arbeit inspiriert, denken Sie bitte daran, es wie folgt zu zitieren:
@inproceedings{
pfrommer2023asymmetric,
title={Uneven Licensed Robustness by way of Function-Convex Neural Networks},
writer={Samuel Pfrommer and Brendon G. Anderson and Julien Piet and Somayeh Sojoudi},
booktitle={Thirty-seventh Convention on Neural Info Processing Programs},
12 months={2023}
}