Eines Tages sagte ein Datenwissenschaftler, dass die Ridge-Regression ein kompliziertes Modell sei. Weil er sah, dass die Trainingsformel komplizierter ist.
Nun ja, genau das ist mein Ziel Maschinelles Lernen „Adventskalender“um diese Artwork von Komplexität zu verdeutlichen.
Wir werden additionally über bestrafte Versionen der linearen Regression sprechen.
- Zuerst werden wir sehen, warum die Regularisierung oder Bestrafung notwendig ist, und wir werden sehen, wie das Modell modifiziert wird
- Anschließend werden wir verschiedene Arten der Regularisierung und ihre Auswirkungen untersuchen.
- Wir werden das Modell auch mit Regularisierung trainieren und verschiedene Hyperparameter testen.
- Wir werden auch eine weitere Frage dazu stellen, wie die Gewichte im Strafzeitraum zu gewichten sind. (verwirrt? Du wirst sehen)
Lineare Regression und ihre „Bedingungen“
Wenn wir über lineare Regression sprechen, wird oft erwähnt, dass einige Bedingungen erfüllt sein sollten.
Vielleicht haben Sie schon einmal Aussagen gehört wie:
- Die Residuen sollten Gauß-förmig sein (manchmal wird dies mit dem Ziel verwechselt, das Gauß-förmig ist, was falsch ist).
- Die erklärenden Variablen sollten nicht kollinear sein
In der klassischen Statistik sind diese Bedingungen für die Schlussfolgerung erforderlich. Beim maschinellen Lernen liegt der Schwerpunkt auf der Vorhersage, sodass diese Annahmen weniger zentral sind, die zugrunde liegenden Probleme jedoch weiterhin bestehen.
Hier sehen wir ein Beispiel für die Kollinearität zweier Merkmale und machen sie völlig gleich.
Und wir haben die Beziehung: y = x1 + x2 und x1 = x2
Ich weiß, wenn sie völlig gleich sind, können wir einfach Folgendes tun: y=2*x1. Die Idee dahinter ist aber, dass sie sehr ähnlich sein können und wir daraus immer ein Modell erstellen können, oder?
Was ist dann das Drawback?
Wenn Merkmale perfekt kollinear sind, ist die Lösung nicht eindeutig. Hier ist ein Beispiel im Screenshot unten.
y = 10000*x1 – 9998*x2

Und wir können feststellen, dass die Norm der Koeffizienten riesig ist.
Die Idee besteht additionally darin, die Norm der Koeffizienten zu begrenzen.
Und nach Anwendung der Regularisierung ist das konzeptionelle Modell dasselbe!
Das ist richtig. Die Parameter der linearen Regression werden geändert. Aber das Modell ist das gleiche.
Verschiedene Versionen der Regularisierung
Die Idee besteht additionally darin, den MSE und die Norm der Koeffizienten zu kombinieren.
Anstatt nur den MSE zu minimieren, versuchen wir, die Summe der beiden Terme zu minimieren.
Welche Norm? Wir können mit den Normen L1 und L2 arbeiten oder sie sogar kombinieren.
Dafür gibt es drei klassische Möglichkeiten und die entsprechenden Modellnamen.
Ridge-Regression (L2-Strafe)
Die Ridge-Regression fügt eine Strafe hinzu quadrierte Werte der Koeffizienten.
Intuitiv:
- Große Koeffizienten werden stark bestraft (aufgrund des Quadrats)
- Koeffizienten werden gegen Null gedrückt
- aber sie werden nie genau Null
Wirkung:
- Alle Funktionen bleiben im Modell erhalten
- Die Koeffizienten sind glatter und stabiler
- sehr wirksam gegen Kollinearität
Grat schrumpftwählt aber nicht aus.

Lasso-Regression (L1-Strafe)
Lasso nutzt einen anderen Elfmeter: den absoluter Wert der Koeffizienten.
Diese kleine Änderung hat eine große Konsequenz.
Mit Lasso:
- einige Koeffizienten können werden genau Null
- Das Modell ignoriert automatisch einige Funktionen
Deshalb wird LASSO so genannt, denn es steht für Geringster absoluter Schrumpfungs- und Auswahloperator.
- Operator: Es bezieht sich auf den zur Verlustfunktion hinzugefügten Regularisierungsoperator
- Am wenigsten: Es wird aus einem Regressionsrahmen der kleinsten Quadrate abgeleitet
- Absolute: Es wird der Absolutwert der Koeffizienten verwendet (L1-Norm)
- Schwindung: Es schrumpft die Koeffizienten gegen Null
- Auswahl: Es kann einige Koeffizienten genau auf Null setzen und so eine Merkmalsauswahl durchführen
Wichtige Nuance:
- Wir können sagen, dass das Modell immer noch die gleiche Anzahl von Koeffizienten hat
- aber einige von ihnen werden während des Trainings gezwungen, auf Null zu gehen
Die Modellform bleibt unverändert, aber Lasso entfernt Options effektiv, indem es die Koeffizienten auf Null setzt.

3. Elastisches Netz (L1 + L2)
Elastic Internet ist ein Kombination von Ridge und Lasso.
Es verwendet:
- eine L1-Strafe (wie Lasso)
- und eine L2-Strafe (wie Ridge)
Warum sie kombinieren?
Weil:
- Lasso kann instabil sein, wenn Options stark korreliert sind
- Ridge handhabt Kollinearität intestine, wählt jedoch keine Options aus
Elastic Internet bietet ein Gleichgewicht zwischen:
- Stabilität
- Schwindung
- spärlich
In realen Datensätzen ist dies oft die praktischste Wahl.
Was sich wirklich ändert: Modell, Ausbildung, Tuning
Betrachten wir dies aus der Sicht des maschinellen Lernens.
Das Modell ändert sich nicht wirklich
Für die ModellFür alle regulierten Versionen schreiben wir immer noch:
y =ax + b.
- Gleiche Anzahl von Koeffizienten
- Gleiche Vorhersageformel
- Die Koeffizienten werden jedoch unterschiedlich sein.
Aus einer bestimmten Perspektive sind Ridge, Lasso und Elastic Internet dies keine unterschiedlichen Modelle.
Der Ausbildung Das Prinzip ist auch das gleiche
Wir weiterhin:
- Definieren Sie eine Verlustfunktion
- minimieren Sie es
- Berechnen Sie Farbverläufe
- Koeffizienten aktualisieren
Der einzige Unterschied ist:
- Die Verlustfunktion enthält jetzt einen Strafterm
Das ist es.
Die Hyperparameter werden hinzugefügt (das ist der eigentliche Unterschied)
Bei der linearen Regression haben wir keine Kontrolle über die „Komplexität“ des Modells.
- Standardmäßige lineare Regression: kein Hyperparameter
- Grat: ein Hyperparameter (Lambda)
- Lasso: ein Hyperparameter (Lambda)
- Elastisches Netz: zwei Hyperparameter
- eine für die Gesamtstärke der Regularisierung
- eine, um L1 vs. L2 auszubalancieren
Additionally:
- Die standardmäßige lineare Regression muss nicht angepasst werden
- Bestrafte Regressionen tun dies
Aus diesem Grund wird die standardmäßige lineare Regression oft als „nicht wirklich maschinelles Lernen“ angesehen, während dies bei regulierten Versionen eindeutig der Fall ist.
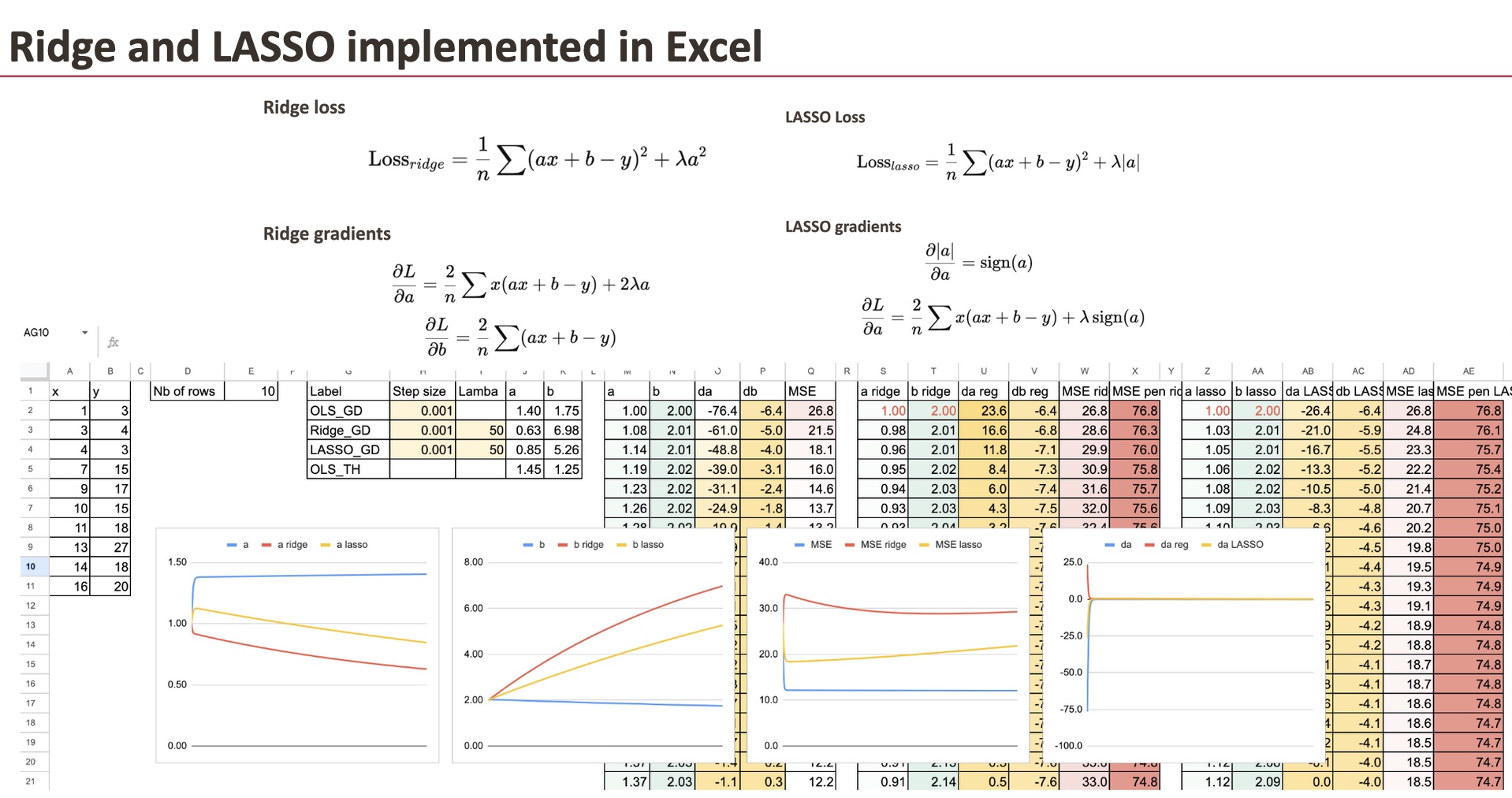
Implementierung regulierter Farbverläufe
Wir behalten den Gradientenabstieg der OLS-Regression als Referenz bei und müssen für die Ridge-Regression nur den Regularisierungsterm für den Koeffizienten hinzufügen.
Wir werden einen einfachen Datensatz verwenden, den ich generiert habe (derselbe, den wir bereits für die lineare Regression verwendet haben).
Wir können sehen, dass sich die drei „Modelle“ hinsichtlich der Koeffizienten unterscheiden. Und das Ziel in diesem Kapitel besteht darin, den Gradienten für alle Modelle zu implementieren und sie zu vergleichen.

Grat mit bestraftem Gefälle
Erstens können wir dies für Ridge tun, und wir müssen nur den Gradienten von a ändern.
Dies bedeutet jedoch nicht, dass sich der Wert b nicht ändert, da der Gradient von b bei jedem Schritt auch von a abhängt.

LASSO mit bestraftem Gefälle
Dann können wir dasselbe für LASSO tun.
Und der einzige Unterschied ist auch die Steigung von a.
Für jedes Modell können wir auch den MSE und den regulierten MSE berechnen. Es ist sehr befriedigend zu sehen, wie sie im Laufe der Iterationen abnehmen.

Vergleich der Koeffizienten
Jetzt können wir den Koeffizienten a für alle drei Modelle visualisieren. Um die Unterschiede zu erkennen, geben wir sehr große Lambdas ein.

Einfluss von Lambda
Für einen großen Lambda-Wert werden wir sehen, dass der Koeffizient a klein wird.
Und wenn Lambda LASSO extrem groß wird, dann erhalten wir theoretisch den Wert 0 für a. Numerisch müssen wir den Gradientenabstieg verbessern.

Regularisierte logistische Regression?
Wir haben gestern die logistische Regression gesehen und eine Frage, die wir stellen können, ist, ob sie auch reguliert werden kann. Wenn ja, wie heißen sie?
Die Antwort lautet natürlich: Ja, die logistische Regression kann reguliert werden
Es gilt genau die gleiche Idee.
Logistische Regression kann auch sein:
- L1 bestraft
- L2 bestraft
- Elastic Internet bestraft
Es gibt keine besonderen Namen wie „Ridge Logistic Regression“ im allgemeinen Sprachgebrauch.
Warum?
Denn das Konzept ist nicht mehr neu.
In der Praxis können Sie in Bibliotheken wie scikit-learn einfach Folgendes angeben:
- die Verlustfunktion
- die Artwork der Strafe
- die Regularisierungsstärke
Die Benennung battle wichtig, als die Idee neu battle.
Heutzutage ist die Regularisierung nur noch eine Standardoption.
Weitere Fragen, die wir stellen können:
- Ist eine Regularisierung immer sinnvoll?
- Wie wirkt sich die Skalierung von Options auf die Leistung der regulierten linearen Regression aus?
Abschluss
Ridge und Lasso ändern nicht das lineare Modell selbst, sondern die Artwork und Weise, wie die Koeffizienten gelernt werden. Durch das Hinzufügen einer Strafe begünstigt die Regularisierung stabile und sinnvolle Lösungen, insbesondere wenn Merkmale korreliert sind. Wenn man diesen Prozess Schritt für Schritt in Excel betrachtet, wird deutlich, dass diese Methoden nicht komplexer, sondern nur kontrollierter sind.