werden oft als Black Containers dargestellt.
Ebenen, Aktivierungen, Farbverläufe, Backpropagation … es kann sich überwältigend anfühlen, insbesondere wenn alles hinter mannequin.match() verborgen ist.
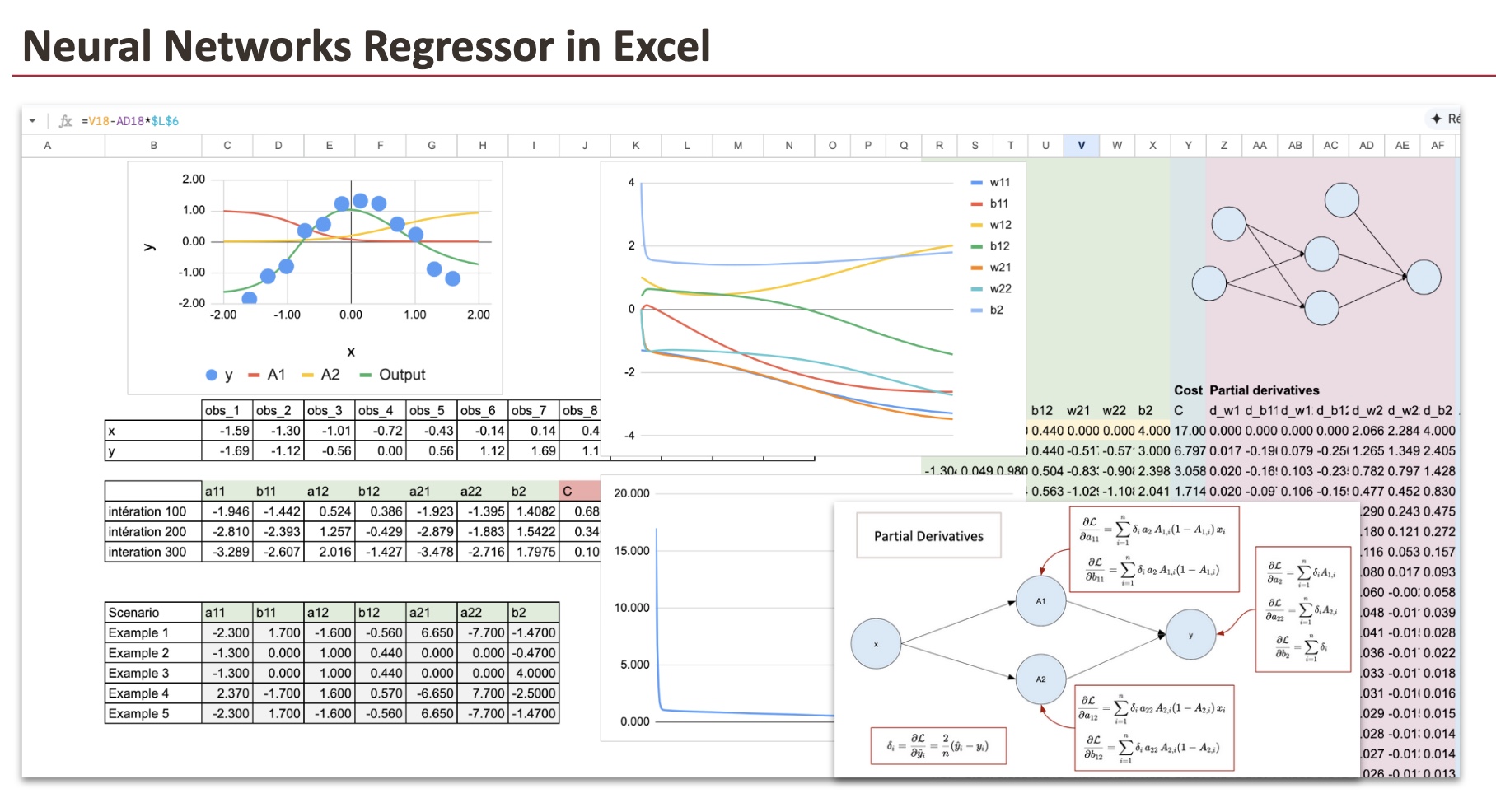
Wir werden eine bauen Regressor für neuronale Netze von Grund auf mit Excel erstellen. Jede Berechnung wird explizit sein. Jeder Zwischenwert wird sichtbar sein. Nichts wird verborgen bleiben.
Am Ende dieses Artikels werden Sie verstehen, wie ein neuronales Netzwerk eine Regression durchführt, wie die Vorwärtsausbreitung funktioniert und wie das Modell nichtlineare Funktionen mit nur wenigen Parametern annähern kann.
Bevor Sie beginnen, sollten Sie sich zunächst die Implementierung von ansehen, wenn Sie meine vorherigen Artikel noch nicht gelesen haben lineare Regression Und Logistische Regression.
Sie werden sehen, dass ein neuronales Netzwerk kein neues Objekt ist. Es ist eine natürliche Erweiterung dieser Modelle.
Wie üblich werden wir diese Schritte befolgen:
- Zunächst schauen wir uns an, wie das Modell eines Neural Community Regressor funktioniert. Bei neuronalen Netzen wird dieser Schritt Vorwärtsausbreitung genannt.
- Dann trainieren wir diese Funktion mithilfe des Gradientenabstiegs. Dieser Vorgang wird Backpropagation genannt.
1. Vorwärtsausbreitung
In diesem Teil definieren wir unser Modell und implementieren es dann in Excel, um zu sehen, wie die Vorhersage funktioniert.
1.1 Ein einfacher Datensatz
Wir werden einen sehr einfachen Datensatz verwenden, den ich generiert habe. Es besteht aus nur 12 Beobachtungen und einem einzigen Merkmal.
Wie Sie sehen, steht die Zielvariable in einer nichtlinearen Beziehung zu x.
Und für diesen Datensatz verwenden wir zwei Neuronen in der verborgenen Schicht.

1.2 Struktur des neuronalen Netzwerks
Unser beispielhaftes neuronales Netzwerk hat:
- Eine Eingabeebene mit dem Characteristic x als Eingabe
- Eine verborgene Schicht mit zwei Neuronen in der verborgenen Schicht, und diese beiden Neuronen ermöglichen es uns, eine nichtlineare Beziehung herzustellen
- Die Ausgabeschicht ist nur eine lineare Regression
Hier ist das Diagramm, das dieses neuronale Netzwerk darstellt, zusammen mit allen Parametern, die geschätzt werden müssen. Es gibt insgesamt 7 Parameter.
Versteckte Ebene:
- a11: Gewicht von x bis zum versteckten Neuron 1
- b11: Bias des versteckten Neurons 1
- a12: Gewicht von x bis zum versteckten Neuron 2
- b12: Bias des versteckten Neurons 2
Ausgabeebene:
- a21: Gewicht vom versteckten Neuron 1 bis zur Ausgabe
- a22: Gewicht vom versteckten Neuron 2 bis zur Ausgabe
- b2: Ausgabeverzerrung
Im Kern ist ein neuronales Netzwerk nur eine Funktion. Eine zusammengesetzte Funktion.
Wenn man es explizit schreibt, ist daran nichts Geheimnisvolles.

Normalerweise stellen wir diese Funktion mit einem Diagramm aus „Neuronen“ dar.
Meiner Meinung nach lässt sich dieses Diagramm am besten interpretieren visuelle Darstellung einer zusammengesetzten mathematischen Funktionnicht als Behauptung, dass es buchstäblich die Funktionsweise biologischer Neuronen reproduziert.

Warum funktioniert diese Funktion?
Jedes Sigmoid verhält sich wie eine glatte Stufe.
Mit zwei Sigmoiden kann das Modell die Ausgabekurve vergrößern, verkleinern, biegen und abflachen.
Durch die lineare Kombination kann das Netzwerk glatte, nichtlineare Kurven annähern.
Aus diesem Grund gilt für diesen Datensatz: Zwei Neuronen reichen bereits aus. Aber könnten Sie einen Datensatz finden, für den diese Struktur nicht geeignet ist?
1.3 Implementierung der Funktion in Excel
In diesem Abschnitt gehen wir davon aus, dass die 7 Koeffizienten bereits gefunden wurden. Und dann können wir die Formel, die wir gerade gesehen haben, umsetzen.
Um das neuronale Netzwerk zu visualisieren, können wir neue kontinuierliche Werte von x im Bereich von -2 bis 2 mit einer Schrittweite von 0,02 verwenden.
Hier ist der Screenshot, und wir können sehen, dass die endgültige Funktion recht intestine zur Kind der Eingabedaten passt.

2. Backpropagation (Gradientenabstieg)
Zu diesem Zeitpunkt ist das Modell vollständig definiert.
Da es sich um ein Regressionsproblem handelt, verwenden wir den MSE (mittlerer quadratischer Fehler), genau wie bei einer linearen Regression.
Jetzt müssen wir die 7 Parameter finden minimieren die MSE.
2.1 Particulars des Backpropagation-Algorithmus
Das Prinzip ist einfach. ABER da es viele zusammengesetzte Funktionen und viele Parameter gibt, müssen wir mit den Ableitungen organisiert sein.
Ich werde nicht alle 7 partiellen Ableitungen explizit ableiten. Ich gebe nur die Ergebnisse bekannt.

Wie wir sehen können, gibt es den Fehlerterm. Um den gesamten Prozess umzusetzen, müssen wir dieser Schleife folgen:
- Initialisieren Sie die Gewichte,
- Berechnen Sie die Ausgabe (Vorwärtsausbreitung),
- Berechnen Sie den Fehler,
- Berechnen Sie Gradienten mithilfe partieller Ableitungen.
- Aktualisieren Sie die Gewichte,
- bis zur Konvergenz wiederholen.
2.2 Initialisierung
Beginnen wir damit, den Eingabedatensatz in ein Spaltenformat zu bringen, das die Implementierung der Formeln in Excel erleichtert.

Theoretisch können wir mit Zufallswerten für die Initialisierung der Parameterwerte beginnen. In der Praxis kann die Anzahl der Iterationen jedoch groß sein, um eine vollständige Konvergenz zu erreichen. Und da die Kostenfunktion nicht konvex ist, können wir in einem lokalen Minimal stecken bleiben.
Wir müssen additionally die Anfangswerte „mit Bedacht“ wählen. Ich habe einige für Sie vorbereitet. Sie können kleine Änderungen vornehmen, um zu sehen, was passiert.

2.3 Vorwärtsausbreitung
In den Spalten von AG bis BP führen wir die Vorwärtsausbreitungsphase durch. Wir berechnen zuerst A1 und A2, gefolgt von der Ausgabe. Dies sind die gleichen Formeln, die im früheren Teil der Vorwärtsausbreitung verwendet wurden.
Um die Berechnungen zu vereinfachen und überschaubarer zu machen, führen wir die Berechnungen für jede Beobachtung separat durch. Das bedeutet, dass wir 12 Spalten für jede verborgene Ebene (A1 und A2) und die Ausgabeebene haben. Anstatt eine Summationsformel zu verwenden, berechnen wir die Werte für jede Beobachtung einzeln.
Um den for-Schleifenprozess während der Gradientenabstiegsphase zu erleichtern, organisieren wir den Trainingsdatensatz in Spalten und können dann die Formel in Excel zeilenweise erweitern.

2.4 Fehler und die Kostenfunktion
In den Spalten BQ bis CN können wir nun die Werte der Kostenfunktion berechnen.

2.5 Partielle Ableitungen
Wir werden 7 partielle Ableitungen berechnen, die den Gewichten unseres neuronalen Netzwerks entsprechen. Für jede dieser partiellen Ableitungen müssen wir die Werte für alle 12 Beobachtungen berechnen, was insgesamt 84 Spalten ergibt. Wir haben uns jedoch bemüht, diesen Prozess zu vereinfachen, indem wir das Blatt zur Vereinfachung der Verwendung mit Farbcodierungen und Formeln versehen haben.

Wir beginnen additionally mit der Ausgabeebene für die Parameter: a21, a22 und b2. Wir finden sie in den Spalten von CO bis DX.

Dann können wir die Parameter a11 und a12 in den Spalten DY bis EV finden:

Und schließlich verwenden wir für die Bias-Parameter b11 und b12 die Spalten EW bis FT.

Und zum Abschluss summieren wir alle partiellen Ableitungen der 12 Beobachtungen. Diese aggregierten Farbverläufe sind übersichtlich in Spalten angeordnet Z bis AF. Die Parameteraktualisierungen werden dann spaltenweise durchgeführt R bis Xunter Verwendung dieser Werte.

2.6 Visualisierung der Konvergenz
Um den Trainingsprozess besser zu verstehen, visualisieren wir mithilfe eines Diagramms, wie sich die Parameter während des Gradientenabstiegs entwickeln. Gleichzeitig wird die Abnahme der Kostenfunktion verfolgt Spalte Ywodurch die Konvergenz des Modells deutlich sichtbar wird.

Abschluss
Ein Regressor für neuronale Netze ist keine Zauberei.
Es handelt sich lediglich um eine Zusammensetzung elementarer Funktionen, die durch eine bestimmte Anzahl von Parametern gesteuert und durch Minimierung eines genau definierten mathematischen Ziels trainiert werden.
Durch den expliziten Aufbau des Modells in Excel wird jeder Schritt sichtbar. Vorwärtsausbreitung, Fehlerberechnung, partielle Ableitungen und Parameteraktualisierungen sind keine abstrakten Konzepte mehr, sondern konkrete Berechnungen, die Sie überprüfen und ändern können.
Die vollständige Implementierung unseres neuronalen Netzwerks, von der Vorwärtsausbreitung bis zur Rückwärtsausbreitung, ist nun abgeschlossen. Wir empfehlen Ihnen, zu experimentieren, indem Sie den Datensatz, die anfänglichen Parameterwerte oder die Lernrate ändern und beobachten, wie sich das Modell während des Trainings verhält.
Durch diese praktische Übung haben wir gesehen, wie Gradienten das Lernen vorantreiben, wie Parameter iterativ aktualisiert werden und wie sich ein neuronales Netzwerk nach und nach an die Daten anpasst. Genau das passiert in modernen Bibliotheken für maschinelles Lernen, nur versteckt hinter ein paar Codezeilen.
Sobald man es so versteht, sind neuronale Netze keine Black Containers mehr.