Lineare Transformationen mit Köcher animieren

Der Wissenschaftler bedeutet unweigerlich, an mehreren Abstraktionsebenen, vorbemosen Abstraktionen von Code und Mathematik zu arbeiten. Dies ist großartig, denn so können Sie schnell erstaunliche Ergebnisse erzielen. Aber manchmal ist es intestine beraten, eine Sekunde innehalten und darüber nachdenken, was tatsächlich hinter einer ordentlichen Schnittstelle passiert. Dieser Nachdenkensprozess wird häufig durch Visualisierungen unterstützt. In diesem Artikel möchte ich präsentieren, wie animierte Köcherplots dazu beitragen können, über lineare Transformationen nachzudenken, die häufig in der Dunkelheit von Algorithmen für maschinelles Lernen und zugehörigen Schnittstellen zuverlässig wegfahren. Am Ende können wir Konzepte wie die Zersetzung von Singular Worth mit unserem Köcherplot visualisieren.

Zeichnen Sie statische Köcherdiagramme

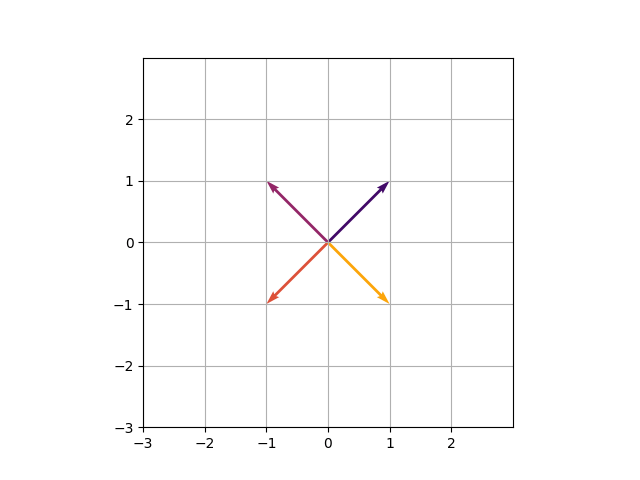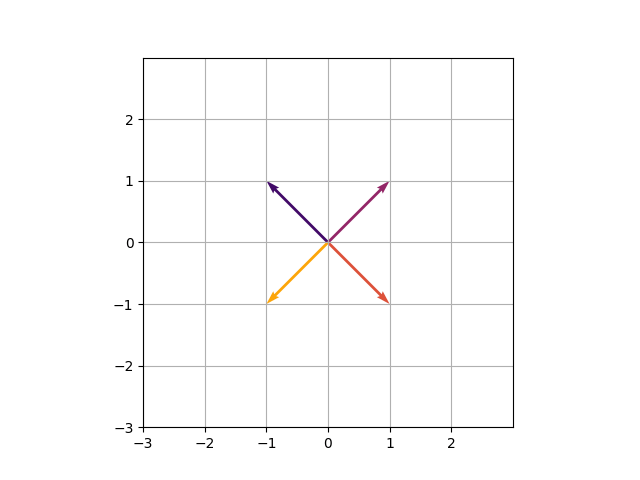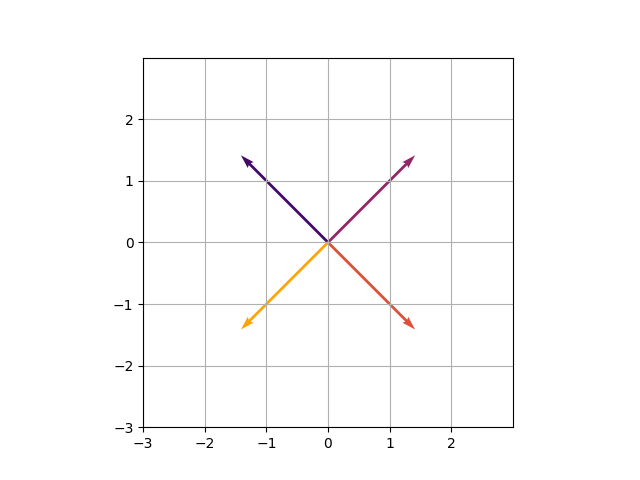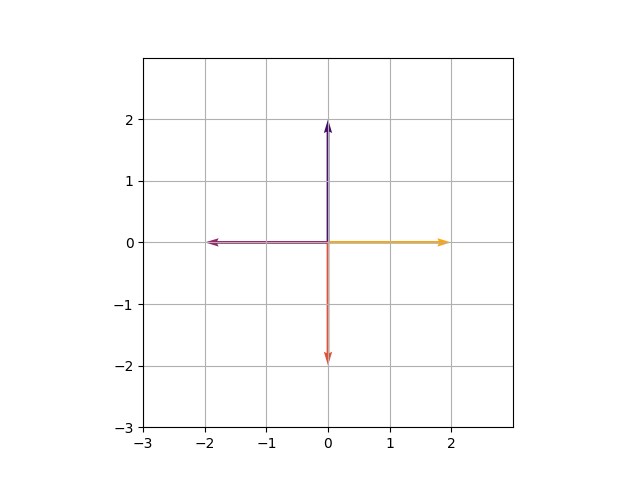
Eine Köcherhandlung aus dem matplotlib Das Python -Paket ermöglicht es uns, Pfeile zu zeichnen (was in unserem Fall Vektoren darstellt). Schauen wir uns zunächst eine statische Köcherung an:

Wir können die Transformationsmatrix direkt aus dem Bild ableiten, indem wir die Zielpositionen der beiden Basisvektoren betrachten. Der erste Basisvektor beginnt an Place (1, 0) und landet auf (1, 1), während der zweite Basisvektor von (0, 1) bis (-1, 1) bewegt. Daher ist die Matrix, die diese Transformation beschreibt,:

(
start {pmatrix}
1 & -1
1 & 1
finish {pmatrix}
)

Visuell entspricht dies einer Rotation gegen den Uhrzeigersinn um 45 Grad (oder ( pi/4 ) in Radian und eine leichte Dehnung (durch den Faktor ( sqrt {2} )).

Schauen wir uns mit diesen Informationen an, wie dies mit dem Quimer implementiert wird (beachten Sie, dass ich einen Boilerplate -Code wie Skalierung der Achse weglässt):

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm

def quiver_plot_base_vectors(transformation_matrix: np.ndarray):
    # Outline vectors
    basis_i = np.array((1, 0))
    basis_j = np.array((0, 1))
    i_transformed = transformation_matrix(:, 0)
    j_transformed = transformation_matrix(:, 1)
    
    # plot vectors with quiver-function
    cmap = cm.inferno
    fig, ax = plt.subplots()
    ax.quiver(0, 0, basis_i(0), basis_i(1), 
        shade=cmap(0.2), 
        scale=1, 
        angles="xy", 
        scale_units="xy", 
        label="i", 
        alpha=0.3)
    ax.quiver(0, 0, i_transformed(0), i_transformed(1), 
        shade=cmap(0.2), 
        scale=1,   
        angles="xy",  
        scale_units="xy", 
        label="i_transformed")
    ax.quiver(0, 0, basis_j(0), basis_j(1), 
        shade=cmap(0.5), 
        scale=1, 
        angles="xy", 
        scale_units="xy", 
        label="j", 
        alpha=0.3)
    ax.quiver(0, 0, j_transformed(0), j_transformed(1), 
        shade=cmap(0.5), 
        scale=1, 
        angles="xy", 
        scale_units="xy", 
        label="j_transformed")

if __name__ == "__main__":
    matrix = np.array((
        (1, -1),
        (1, 1)  
    ))
    quiver_plot_base_vectors(matrix)

Wie Sie sehen können, haben wir ein Köcher professional Vektor definiert. Dies ist nur für veranschaulichende Zwecke. Wenn wir uns die Signatur der Köcherfunktion ansehen – quiver((X, Y), U, V, (C), /, **kwargs) – Wir können beobachten, dass u und v Numpy -Arrays als Eingabe nutzen, was besser ist als die Bereitstellung von Skalarwerten. Lassen Sie uns diese Funktion mit nur einem Köcheraufruf neu ausführen. Lassen Sie uns außerdem einen Vektor v = (1,5, -0,5) hinzufügen, um die darauf angewendete Transformation anzuzeigen.

def quiver_plot(transformation_matrix: np.ndarray, vector: np.ndarray):
    # Outline vectors
    basis_i = np.array((1, 0))
    basis_j = np.array((0, 1))
    i_transformed = transformation_matrix(:, 0)
    j_transformed = transformation_matrix(:, 1)
    vector_transformed = transformation_matrix @ vector
    U, V = np.stack(
        (
            basis_i, i_transformed,
            basis_j, j_transformed,
            vector, vector_transformed,
        ),
        axis=1)

    # Draw vectors
    shade = np.array((.2, .2, .5, .5, .8, .8))
    alpha = np.array((.3, 1.0, .3, 1.0, .3, 1.0))
    cmap = cm.inferno
    fig, ax = plt.subplots()
    ax.quiver(np.zeros(6), np.zeros(6), U, V,
        shade=cmap(shade),
        alpha=alpha,
        scale=1,
        angles="xy",
        scale_units="xy",
    )

if __name__ == "__main__":
    matrix = np.sqrt(2) * np.array((
        (np.cos(np.pi / 4), np.cos(3 * np.pi / 4)),
        (np.sin(np.pi / 4), np.sin(3 * np.pi / 4))
    ))
    vector = np.array((1.5, -0.5))
    quiver_plot(matrix, vector)

Dies ist viel kürzer und bequem als das erste Beispiel. Was wir hier getan haben, struggle, jeden Vektor horizontal das folgende Array zu stapeln:

Die erste Zeile entspricht dem U-Parameter von quiver und die zweite nach V., während die Spalten unsere Vektoren halten, wobei ( vec {i} ) der erste Basisvektor ist, ist ( vec {j} ) der zweite und ( vec {v} ) ist unser individueller Vektor. Die Indizes B und A stehen für vor Und nach (dh ob Die lineare Transformation wird angewendet oder nicht). Schauen wir uns die Ausgabe an:

Wenn Sie einen zweiten Blick auf den Code werfen, könnte es verwirrt werden, was mit unserer ordentlichen und einfachen Transformationsmatrix passiert ist, die angezeigt wurde:

(
{ scriptSize
M = start {pmatrix}
{1} & {-1}
{1} & {1}
finish {pmatrix} = { sqrt {2}}
start {pmatrix}
{ cos hyperlinks ( frac {1} {4} pi rechts)} & { cos hyperlinks ( frac {3} {4} pi rechts)}
{ sin hyperlinks ( frac {1} {4} pi rechts)} & { sin hyperlinks ( frac {3} {4} pi rechts)}
finish {pmatrix}
}
)

Der Grund ist, dass diese Darstellung nützlich sein wird, wenn wir durch das Hinzufügen von Animationen weitermachen. Die skalare Multiplikation durch die Quadratwurzel von zwei zeigt, wie stark unsere Vektoren gedehnt werden, während die Elemente der Matrix in trigonometrischer Notation umgeschrieben werden, um die Rotation im Einheitskreis darzustellen.

Lass uns animieren

Gründe, Animationen hinzuzufügen, können sauberere Handlungen enthalten, da wir die Geistervektoren loswerden und ein ansprechenderes Erlebnis für Präsentationen schaffen können. Um unsere Handlung mit Animationen zu verbessern, können wir im Matplotlib -Ökosystem bleiben, indem wir die verwenden FuncAnimation() Funktion von matplotlib.animation. Die Funktion nimmt die folgenden Argumente an:

• A matplotlib.determine.Determine Objekt
• eine Aktualisierungsfunktion
• die Anzahl der Frames

Für jeden Body wird die Aktualisierungsfunktion aufgerufen, um eine aktualisierte Model des ersten Kreidels zu erstellen. Weitere Informationen finden Sie unter der offizielle Dokumentation von Matplotlib.

Unter Berücksichtigung dieser Informationen besteht unsere Aufgabe darin, die Logik zu definieren, die in der Aktualisierungsfunktion implementiert werden soll. Beginnen wir einfach mit nur drei Frames und unseren Basisvektoren. Auf Rahmen 0 sind wir im Anfangszustand. Während wir auf dem letzten Rahmen (Rahmen 2) zu der angepassten Matrix M. ankommen müssen. Daher würden wir erwarten, dass wir auf dem Rahmen auf halbem Weg auf dem Rahmen sind. Da die Argumente von ( cos ) und ( sin ) in M ​​die Radians zeigen (dh, wie weit wir auf dem Einheitskreis gereist sind), können wir sie durch zwei Teilen durch zwei Teilen durch zwei Teilen, um die gewünschten Rotation zu erzählen. (Der zweite Vektor erhält ein negatives ( cos ), weil wir jetzt im zweiten Quadranten sind). In ähnlicher Weise müssen wir die Dehnung berücksichtigen, die durch den Skalarfaktor dargestellt wird. Wir tun dies, indem wir die Größenänderung berechnen, die ( sqrt {2} -1 ) ist und die Hälfte dieser Änderung zur anfänglichen Skalierung hinzufügen.

(
{ scriptSize
start {ausgerichtet}
textual content {Body 0:} quad &
start {pmatrix}
cos (0) & cos hyperlinks ( frac { pi} {2} rechts)
sin (0) & sin hyperlinks ( frac { pi} {2} rechts)
finish {pmatrix}
(1em)
textual content {Body 1:} quad &
S cdot start {pmatrix}
cos hyperlinks ( frac {1} {2} cdot frac { pi} {4} rechts) & – cos hyperlinks ( frac {1} {2} cdot frac {3 pi} {4} rechts)
sin hyperlinks ( frac {1} {2} cdot frac { pi} {4} rechts) & sin hyperlinks ( frac {1} {2} cdot frac {3 pi} {4} rechts)
finish {pmatrix}, quad textual content {mit} s = 1 + frac { sqrt {2} – 1} {2}
(1em)
textual content {Body 2:} quad &
sqrt {2} cdot start {pmatrix}
cos hyperlinks ( frac { pi} {4} rechts) & cos hyperlinks ( frac {3 pi} {4} rechts)
sin hyperlinks ( frac { pi} {4} rechts) & sin hyperlinks ( frac {3 pi} {4} rechts)
finish {pmatrix}
finish {ausgerichtet}
}
)

Eine Einschränkung der obigen Erklärung: Sie dient dem Zweck, der Implementierungsidee intuitioniert zu werden, und gilt für die Basisvektoren. Die tatsächliche Implementierung enthält jedoch einige weitere Schritte, z. B. einige Transformationen mit ( arctan ), um das gewünschte Verhalten für alle Vektoren im zweidimensionalen Raum zu erhalten.

Überprüfen wir additionally die Hauptteile der Implementierung. Der vollständige Code kann auf meinem gefunden werden Github.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation
from matplotlib import cm

class AnimationPlotter:
(...)
def animate(self, filename='output/mat_transform.gif'):
        self.initialize_plot()
        anim = animation.FuncAnimation(
            self.fig,
            self.update_quiver,
            frames=self.frames + 1,
            init_func=self.init_quiver,
            blit=True,
        )
        anim.save(filename, author='ffmpeg', fps=self.frames/2)
        plt.shut()
   
if __name__ == "__main__":
    matrix = np.sqrt(2) * np.array((
        (np.cos(np.pi / 4), np.cos(3 * np.pi / 4)),
        (np.sin(np.pi / 4), np.sin(3 * np.pi / 4))
       
    ))
    vector = np.array((1.5, -0.5)).reshape(2, 1)
    transformer = Transformer(matrix)
    animation_plotter = AnimationPlotter(transformer, vector)
    animation_plotter.animate()

Der animate() Die Methode gehört zu einer benutzerdefinierten Klasse, die genannt wird AnimationPlotter. Es tut das, was wir bereits mit den oben angegebenen Eingaben gelernt haben. Die zweite Klasse in der Szene ist eine benutzerdefinierte Klasse Transformerdie sich um die Berechnung der linearen Transformationen und Zwischenvektoren für jeden Body kümmert. Die Hauptlogik liegt in der AnimationPlotter.update_quiver() Und Transformer.get_intermediate_vectors() Methoden und sieht wie folgt aus.

class AnimationPlotter:
    (...)
    def update_quiver(self, body: int):
        incremented_vectors = self.transformer.get_intermediate_vectors(
            body, self.frames
        )
        u = incremented_vectors(0)
        v = incremented_vectors(1)
        self.quiver_base.set_UVC(u, v)
        return self.quiver_base,

class Transformer:
    (...)
    def get_intermediate_vectors(self, body: int, total_frames: int) -> np.ndarray:
         change_in_direction = self.transformed_directions - self.start_directions
         change_in_direction = np.arctan2(np.sin(change_in_direction), np.cos(change_in_direction))
         increment_direction = self.start_directions + change_in_direction * body / total_frames
         increment_magnitude = self.start_magnitudes + (self.transformed_magnitudes - self.start_magnitudes) * body / total_frames
         incremented_vectors = np.vstack((np.cos(increment_direction), np.sin(increment_direction))) @ np.diag(increment_magnitude)
         return incremented_vectors

Was hier passiert, ist, dass für jeden Body die Zwischenvektoren berechnet werden. Dies geschieht durch den Unterschied zwischen Finish- und Startanweisungen (die Vektorwinkel darstellen). Die Änderung der Richtung/des Richtungswinkels wird dann auf den Bereich ((- pi, pi) ) normalisiert und durch ein Verhältnis in die Anfangsrichtung hinzugefügt. Das Verhältnis wird durch den Strom und die Gesamtrahmen bestimmt. Die Größe wird wie bereits beschrieben bestimmt. Schließlich wird der inkrementierte Vektor basierend auf Richtung und Größe berechnet, und dies sehen wir bei jedem Body in der Animation. Durch das Erhöhen der Frames, um 30 oder 60 zu sagen, wird die Animation reibungslos.

Animation Singular Worth Decomposition (SVD)

Schließlich möchte ich zeigen, wie die Einführungsanimation erstellt wurde. Es zeigt, wie 4 Vektoren (jeweils für jeden Quadranten) dreimal nacheinander transformiert werden. In der Tat entsprechen die drei angewendeten Transformationen unserer inzwischen bekannten Transformationsmatrix M von oben, zersetzt jedoch durch die Singularwert-Zersetzung (SVD). Sie können Ihr Kenntnis Das Großer und intuitiver TDS -Artikel. Oder schauen Sie sich an Hier Wenn Sie eine eher mathematischer Lesen vorziehen. Jedoch mit numpy.linalg.svd() Es ist einfach, die SVD unserer Matrix M zu berechnen. Dies führt zu der folgenden Zerlegung:

(
{ scriptSize
start {align}
A vec {v} & = u sigma v^t vec {v} (1em)
sqrt {2} cdot start {pmatrix}
cos hyperlinks ( frac { pi} {4} rechts) & cos hyperlinks ( frac {3 pi} {4} rechts)
sin hyperlinks ( frac { pi} {4} rechts) & sin hyperlinks ( frac {3 pi} {4} rechts)
finish {pmatrix} vec {v} & =
start {pmatrix}
cos hyperlinks ( frac {3 pi} {4} rechts) & cos hyperlinks ( frac {3 pi} {4} rechts)
sin hyperlinks ( frac {- pi} {4} rechts) & sin hyperlinks ( frac { pi} {4} rechts)
finish {pmatrix}
start {pmatrix}
sqrt {2} & 0
0 & sqrt {2}
finish {pmatrix}
start {pmatrix}
-1 & 0
0 & 1
finish {pmatrix} vec {v}
finish {align}
}
)

Beachten Sie, wie die Dehnung der Quadratwurzel durch die mittlere Matrix destilliert wird. Die folgende Animation zeigt, wie dies in Aktion (oder Bewegung) für V = (1,5, -0,5) aussieht.

Am Ende kommt der lila Vektor ( vec {v} ) in beiden Fällen an seiner entschlossenen Place an.

Abschluss

Um es abzuschließen, können wir verwenden quiver() Vektoren im 2D -Bereich anzeigen und mit Hilfe von matplotlib.animation.FuncAnimation(), Fügen Sie ansprechende Animationen oben hinzu. Dies führt zu klaren Visualisierungen linearer Transformationen, die Sie beispielsweise verwenden können, um die zugrunde liegenden Mechanik Ihrer Algorithmen für maschinelles Lernen zu demonstrieren. Fühlen Sie sich frei, mein Repository zu geben und Ihre eigenen Visualisierungen zu implementieren. Ich hoffe, Sie haben die Lektüre genossen!